Як перевірити значущість нахилу регресії

Скажімо, у нас є такий набір даних, який показує квадратні метри та ціни 12 різних будинків:

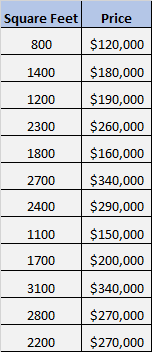
Ми хочемо знати, чи існує значний зв’язок між квадратними метрами та ціною.

Щоб отримати уявлення про те, як виглядають дані, ми спочатку створюємо діаграму розсіювання з квадратними футами на осі X і ціною на осі Y:

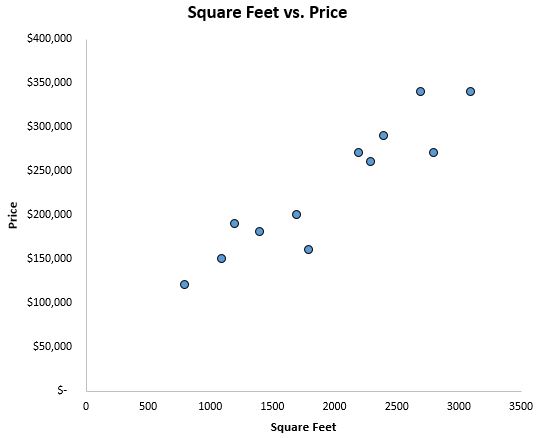
Ми чітко бачимо, що існує позитивна кореляція між квадратними метрами та ціною. Зі збільшенням квадратних метрів ціна будинку також має тенденцію до зростання.

Однак, щоб з’ясувати, чи існує статистично значущий зв’язок між квадратними метрами та ціною, нам потрібно запустити просту лінійну регресію.

Отже, ми виконуємо просту лінійну регресію , використовуючи квадратні фути як предиктор і ціну як відповідь, і отримуємо такий результат:

Незалежно від того, чи виконуєте ви просту лінійну регресію в Excel, SPSS, R чи будь-якому іншому програмному забезпеченні, ви отримаєте результат, подібний до показаного вище.

Пам’ятайте, що проста лінійна регресія дасть лінію найкращого підходу, яка є рівнянням лінії, яка найкраще «відповідає» даним на нашій діаграмі розсіювання. Ця лінія найкращого підходу визначається як:

ŷ = b ₀ + b ₁ x

де ŷ – прогнозоване значення змінної відповіді, b ₀ – відрізок, b ₁ – коефіцієнт регресії, а x – значення змінної предиктора.

Значення b ₀ визначається коефіцієнтом початку координат, який дорівнює 47588,70.

Значення b ₁ визначається коефіцієнтом предикторної змінної Square Feet , який становить 93,57.

Отже, найкраща лінія в цьому прикладі ŷ = 47588,70+ 93,57x

Ось як інтерпретувати цей рядок, який найкраще підходить:

• b ₀ : коли вартість квадратних футів дорівнює нулю, очікувана середня ціна становить 47 588,70 доларів США. (У цьому випадку насправді немає сенсу інтерпретувати перехоплення, оскільки будинок ніколи не може мати нуль квадратних футів)
• b ₁ : за кожен додатковий квадратний фут середнє очікуване зростання ціни становить 93,57 доларів США.

Отже, тепер ми знаємо, що за кожен додатковий квадратний фут середнє очікуване зростання ціни становить 93,57 доларів.

Щоб дізнатися, чи є це збільшення статистично значущим, нам потрібно виконати перевірку гіпотези для B ₁ або побудувати довірчий інтервал для B ₁ .

Примітка . Перевірка гіпотези та довірчий інтервал завжди дають однакові результати.

Побудова довірчого інтервалу для нахилу регресії

Щоб побудувати довірчий інтервал для нахилу регресії, ми використовуємо таку формулу:

Довірчий інтервал = b ₁ +/- (t _{1-∝/2, n-2} ) * (стандартна помилка b ₁ )

золото:

• b ₁ – коефіцієнт нахилу, поданий у результаті регресії
• (t _{1-∝/2, n-2} ) — критичне значення t для рівня довіри 1-∝ із n-2 ступенями свободи, де n — загальна кількість спостережень у нашому наборі даних
• (стандартна помилка b ₁ ) — стандартна помилка b ₁ , наведена в результаті регресії

Для нашого прикладу ось як побудувати 95% довірчий інтервал для B ₁ :

• b ₁ дорівнює 93,57 із результату регресії.
• Оскільки ми використовуємо 95% довірчий інтервал, ∝ = 0,05 і n-2 = 12-2 = 10, тому t _{0,975, 10} дорівнює 2,228 згідно з таблицею розподілу t
• (стандартна помилка _b1 ) дорівнює 11,45 із результату регресії

Таким чином, наш 95% довірчий інтервал для B ₁ становить:

93,57 +/- (2,228) * (11,45) = (68,06, 119,08)

Це означає, що ми на 95% впевнені, що справжнє середнє зростання ціни за кожен додатковий квадратний фут становить від 68,06 до 119,08 доларів США.

Зауважте, що 0 доларів США не входить до цього інтервалу, тому зв’язок між квадратними метрами та ціною є статистично значущим на рівні достовірності 95%.

Виконання перевірки гіпотези для нахилу регресії

Щоб виконати перевірку гіпотези для нахилу регресії, ми виконуємо п’ять стандартних кроків для будь-якої перевірки гіпотези :

Крок 1. Висловіть гіпотези.

Нульова гіпотеза (H0): B ₁ = 0

Альтернативна гіпотеза: (Ha): B ₁ ≠ 0

Крок 2. Визначте рівень значущості для використання.

Оскільки в попередньому прикладі ми побудували 95% довірчий інтервал, тут ми використаємо еквівалентний підхід і виберемо рівень значущості 0,05.

Крок 3. Знайдіть тестову статистику та відповідне значення p.

У цьому випадку статистикою тесту є t = коефіцієнт b ₁ / стандартна помилка b ₁ з n-2 ступенями свободи. Ми можемо знайти ці значення з результату регресії:

Таким чином, тестова статистика t = 92,89 / 13,88 = 6,69.

За допомогою калькулятора оцінки Т до значення Р із оцінкою 6,69 із 10 ступенями свободи та двобічним тестом значення р = 0,000 .

Крок 4. Відкинути або не відхилити нульову гіпотезу.

Оскільки p-значення нижче нашого рівня значущості 0,05, ми відхиляємо нульову гіпотезу.

Крок 5. Інтерпретація результатів.

Оскільки ми відкинули нульову гіпотезу, у нас є достатньо доказів, щоб стверджувати, що справжнє середнє зростання ціни на кожен додатковий квадратний фут не дорівнює нулю.