Як отримати залишки з функції lm() у r
Щоб отримати залишки з функції lm() у R, можна використати такий синтаксис:
fit$residuals
У цьому прикладі припускається, що ми використали функцію lm() для підгонки моделі лінійної регресії та назвали результати підгонкою .
У наступному прикладі показано, як використовувати цей синтаксис на практиці.
Пов’язане: як отримати R-квадрат із функції lm() у R
Приклад: як отримати залишки з lm() у R
Припустимо, що ми маємо наступний кадр даних у R, який містить інформацію про зіграні хвилини, загальну кількість фолів і загальну кількість очок, набраних 10 баскетболістами:
#create data frame df <- data. frame (minutes=c(5, 10, 13, 14, 20, 22, 26, 34, 38, 40), fouls=c(5, 5, 3, 4, 2, 1, 3, 2, 1, 1), points=c(6, 8, 8, 7, 14, 10, 22, 24, 28, 30)) #view data frame df minutes fouls points 1 5 5 6 2 10 5 8 3 13 3 8 4 14 4 7 5 20 2 14 6 22 1 10 7 26 3 22 8 34 2 24 9 38 1 28 10 40 1 30
Припустімо, ми хочемо підібрати таку модель множинної лінійної регресії:
очки = β 0 + β 1 (хвилини) + β 2 (фоли)
Ми можемо використовувати функцію lm() , щоб відповідати цій моделі регресії:
#fit multiple linear regression model
fit <- lm(points ~ minutes + fouls, data=df)
Потім ми можемо ввести fit$residuals , щоб отримати залишки з моделі:
#extract residuals from model
fit$residuals
1 2 3 4 5 6 7
2.0888729 -0.7982137 0.6371041 -3.5240982 1.9789676 -1.7920822 1.9306786
8 9 10
-1.7048752 0.5692404 0.6144057
Оскільки в нашій базі даних було всього 10 спостережень, є 10 залишків – по одному для кожного спостереження.
Наприклад:
- Перше спостереження має залишок 2089 .
- Друге спостереження має залишок -0,798 .
- Третє спостереження має залишок 0,637 .
І так далі.
Потім ми можемо створити графік залишків від підігнаних значень, якщо бажаємо:
#store residuals in variable
res <- fit$residuals
#produce residual vs. fitted plot
plot(fitted(fit), res)
#add a horizontal line at 0
abline(0,0)
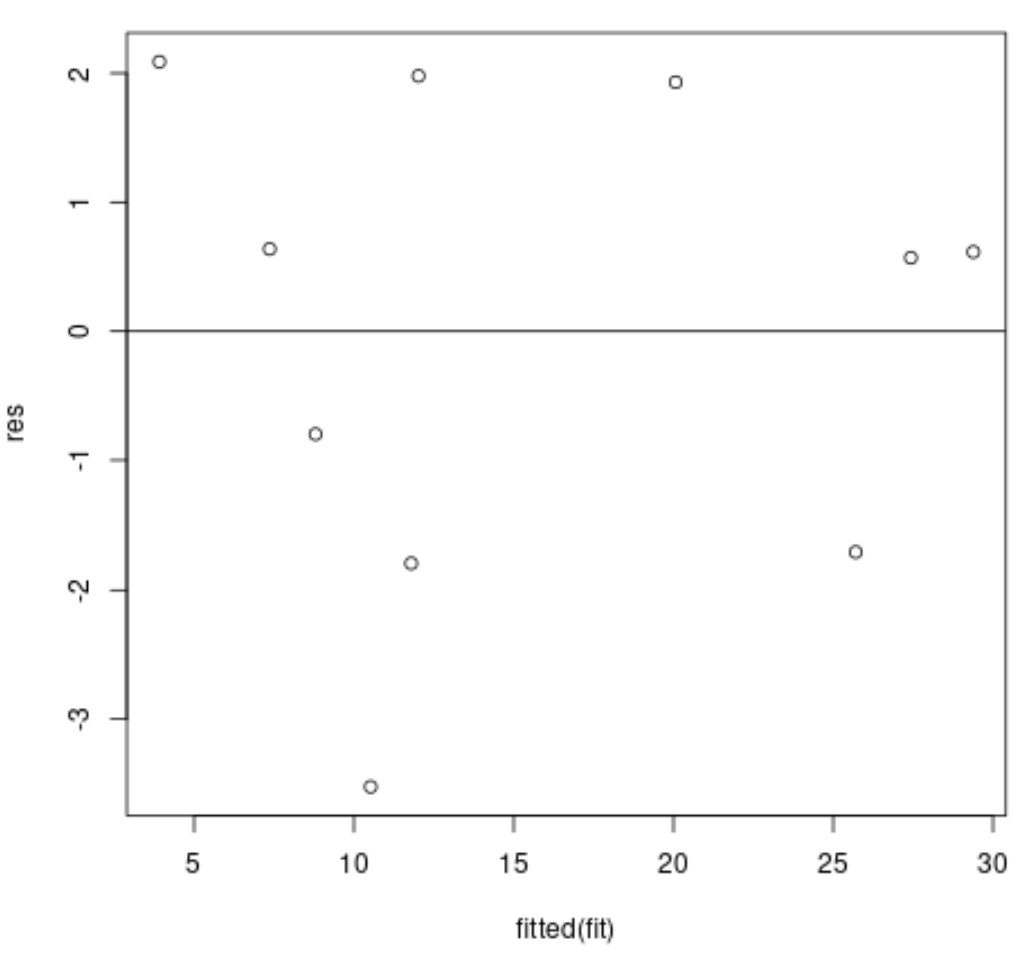
На осі абсцис відображаються підігнані значення, а на осі у – залишки.
В ідеалі залишки мають бути випадковим чином розкидані навколо нуля, без чіткої моделі, щоб гарантувати виконання припущення про гомоскедастичність .
На наведеному вище графіку залишків ми бачимо, що залишки випадково розкидані навколо нуля без чіткого шаблону, що означає, що припущення про гомоскедастичність, ймовірно, виконується.
Додаткові ресурси
У наступних посібниках пояснюється, як виконувати інші типові завдання в R:
Як виконати просту лінійну регресію в R
Як виконати множинну лінійну регресію в R
Як створити ділянку залишків у R