Excel: створіть статистичне порівняння двох наборів даних

Часто вам може знадобитися виконати статистичне порівняння двох наборів даних у Excel, щоб зрозуміти, чим відрізняється розподіл значень у кожному наборі даних.

Існує два поширених способи статистичного порівняння:

Спосіб 1: обчисліть п’ятизначний підсумок кожного набору даних

Ми можемо обчислити п’ятизначний підсумок кожного набору даних, який складається з таких значень:

• Мінімальне значення
• Перший квартиль (25 процентиль)
• Медіана (50-й процентиль)
• Третій квартиль (75-й процентиль)
• Максимум

Обчисливши ці п’ять значень, ми можемо отримати гарне розуміння розподілу значень у кожному наборі даних.

Спосіб 2: обчисліть середнє значення та стандартне відхилення

Більш простий спосіб виконати статистичне порівняння двох наборів даних — обчислити середнє значення та стандартне відхилення кожного набору даних.

Це допомагає нам приблизно зрозуміти, де знаходиться «центральне» значення і який розподіл значень у кожному наборі даних.

У наступному прикладі показано, як використовувати кожен із цих методів на практиці.

Приклад: виконайте статистичне порівняння двох наборів даних у Excel

Припустімо, що ми маємо два набори даних в Excel, які показують результати студентів двох різних класів, отримані на конкретному іспиті:

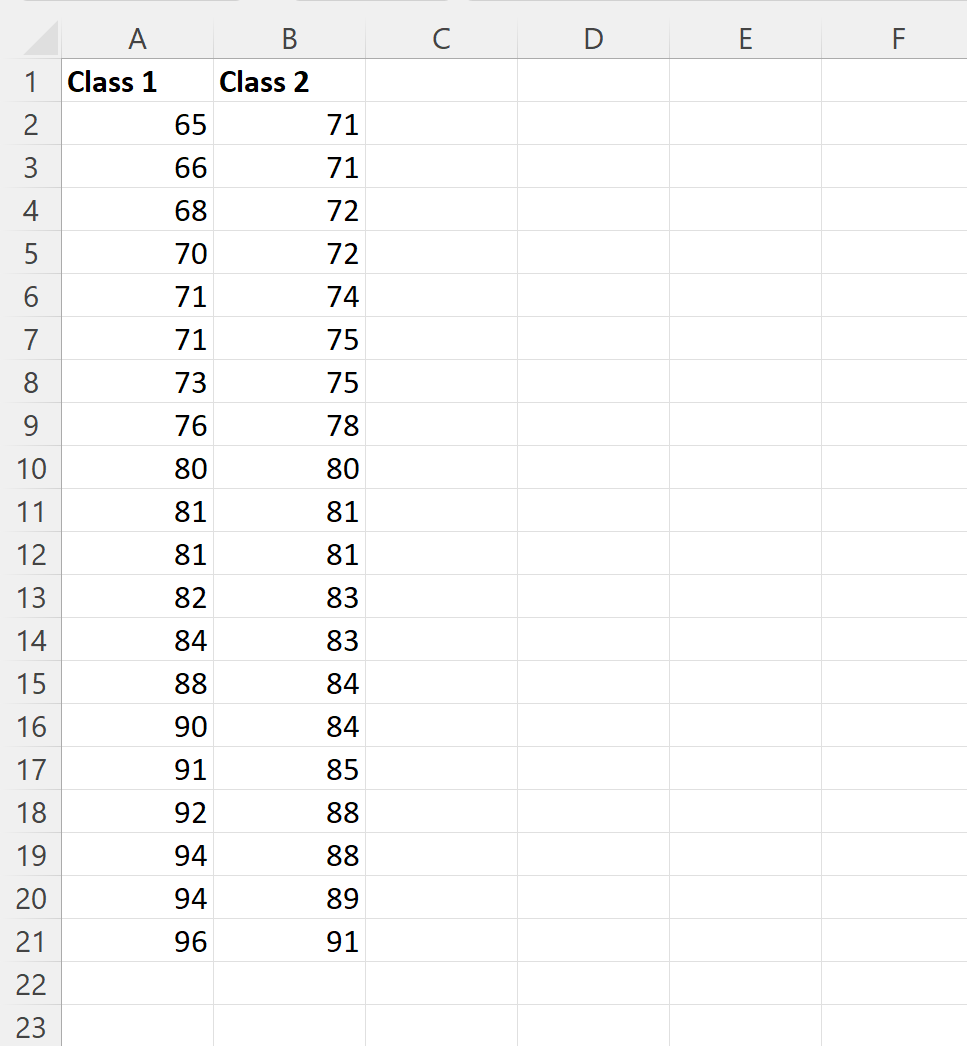
Ми можемо ввести наступні формули в комірки стовпця E, щоб обчислити п’ятизначний підсумок іспитів для 1 класу:

• E2 : =MIN(A2:A21)
• E3 : =КВАРТИЛЬ(A2:A21; 1)
• E4 : =MEDIAN(A2:A21)
• E5 : =КВАРТИЛЬ(A2:A21; 3)
• E6 : =MAX(A2:A21

Потім ми можемо клацнути й перетягнути ці формули праворуч, щоб обчислити ті самі значення для класу 2:

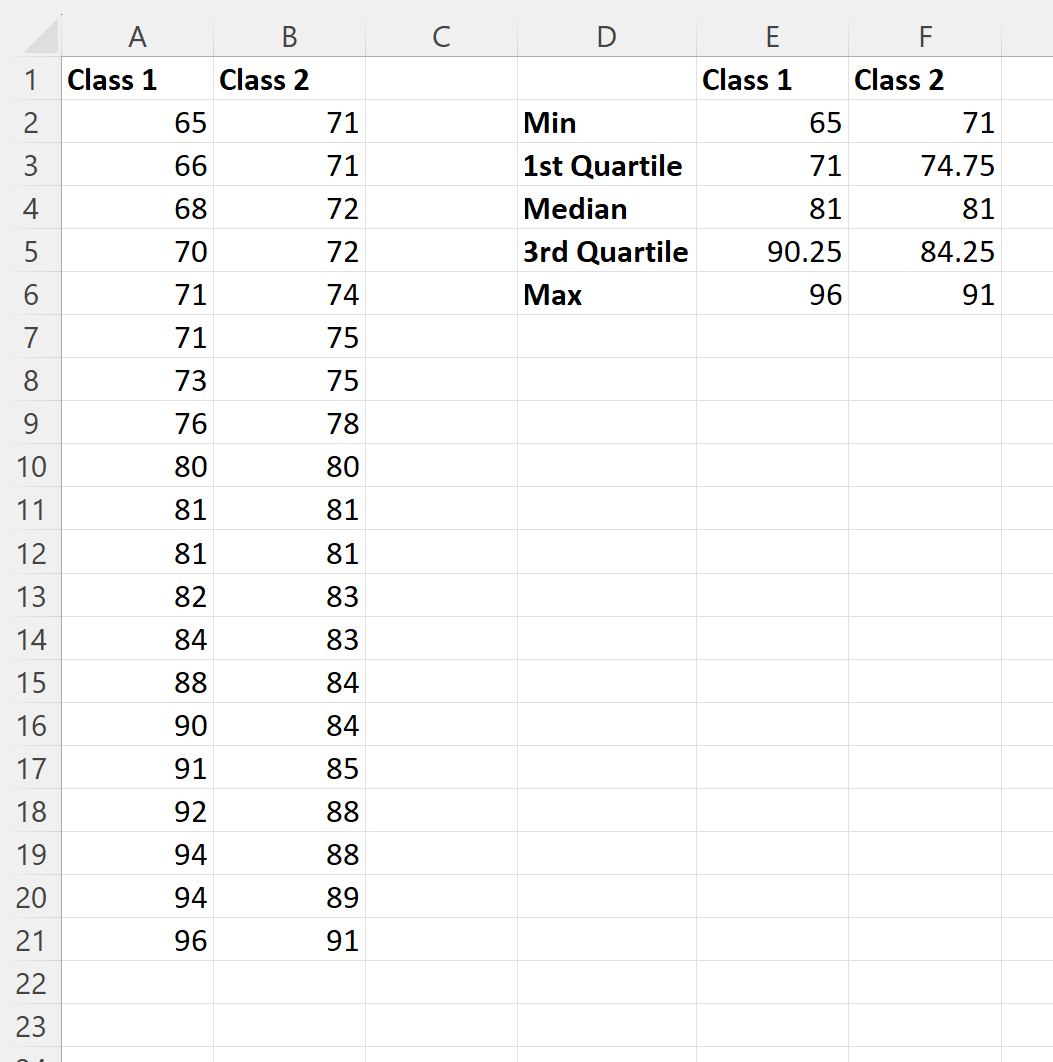
Потім ми можемо ввести такі формули в комірки стовпця E, щоб обчислити середнє значення та стандартне відхилення результатів іспиту для 1 класу:

• E8 : =СЕРЕДНЄ (A2:A21)
• E9 : =ETDEV(A2:A21; 1)

Потім ми можемо клацнути й перетягнути ці формули праворуч, щоб обчислити ті самі значення для класу 2:

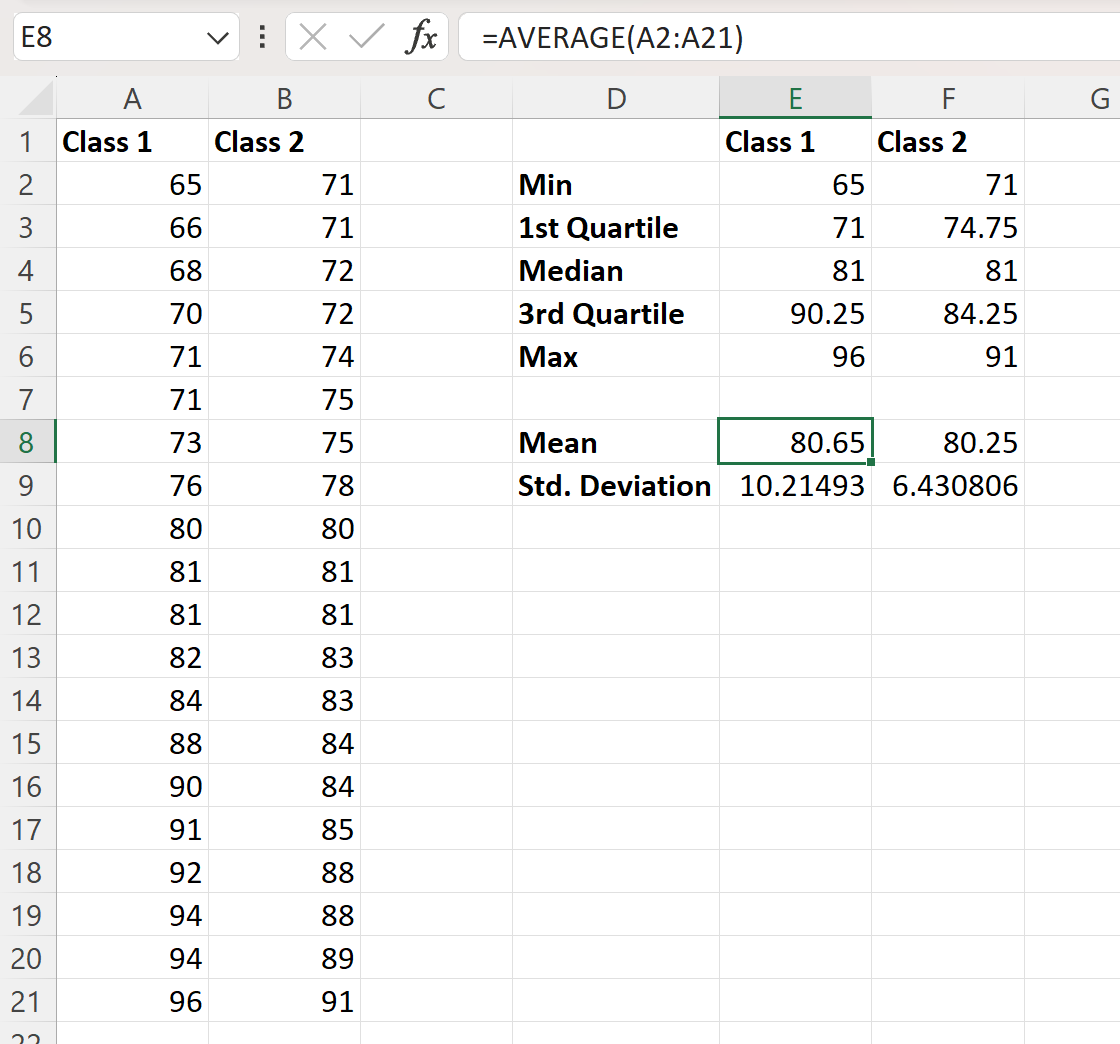
З цього статистичного порівняння двох наборів даних ми можемо зробити наступні висновки:

Висновок 1: обидва набори даних мають однакову «основну» цінність.

Обидва набори даних мають середній іспитовий бал 81. Середні значення відрізняються лише незначно: перший клас має середній іспитовий бал 80,65, другий клас має середній іспитовий бал 80,65, а другий клас має середній іспитовий бал 80,65. 80.65 ‘ огляд 80.25.

Це говорить нам про те, що «основний» або «типовий» іспитовий бал у двох класах подібний.

Висновок 2: перший набір даних має набагато більшу «дисперсію» значень.

Кілька показників говорять нам про те, що результати іспитів першого класу значно розрізнені, ніж результати другого класу.

Наприклад, обсяг класу 1 набагато вищий:

• Діапазон класу 1: 96 – 65 = 31
• Діапазон класу 2: 91 – 71 = 20

Інтерквартильний діапазон класу 1 також значно вищий:

• Інтерквартильний діапазон класу 1: 90,25 – 71 = 19,25
• Інтерквартильний діапазон 2 класу: 84,25 – 74,75 = 9,5

Стандартне відхилення класу 1 також значно вище:

• Стандартне відхилення 1 класу: 10,21
• Стандартне відхилення класу 2: 6,43

Кожен із цих показників говорить нам про те, що розрив в іспитових балах для учнів 1-го класу набагато вищий, ніж для 2-го класу.

Додаткові ресурси

У наступних посібниках пояснюється, як виконувати інші типові операції в Excel:

Як створити зведену таблицю в Excel
Як обчислити медіану по групах в Excel
Як обчислити стандартне відхилення та ігнорувати нуль у Excel