Розмір ефекту: що це таке і чому це важливо
«Статистична значущість — найменш цікава річ у результатах. Вам потрібно описати результати в термінах міри величини – не тільки лікування впливає на людей, але й те, наскільки воно на них впливає. -Джейн В. Гласс
У статистиці ми часто використовуємо p-значення , щоб визначити, чи є статистично значуща різниця між двома групами.
Наприклад, скажімо, ми хочемо знати, чи призводять дві різні методики до різних тестових балів. Отже, ми маємо групу з 20 студентів, які використовують одну техніку навчання для підготовки до тесту, тоді як інша група з 20 студентів використовує іншу техніку навчання. Потім ми даємо кожному студенту той самий тест.
Після виконання двовибіркового t-критерію для визначення різниці середніх значень ми виявили, що p-значення для тесту становить 0,001. Якщо ми використовуємо рівень значущості 0,05, це означає, що існує статистично значуща різниця між середніми результатами двох груп. Отже, техніка навчання впливає на результати тестування.
Однак, хоча p-значення говорить нам про те, що техніка вивчення впливає на результати тестів, воно не говорить нам про величину цього впливу. Щоб зрозуміти це, нам потрібно знати розмір ефекту .
Що таке розмір ефекту?
Розмір ефекту — це спосіб кількісного визначення різниці між двома групами.
Хоча p-значення може сказати нам, чи є статистично значуща різниця між двома групами, розмір ефекту може сказати нам , наскільки велика ця різниця насправді. На практиці знати про величину ефекту набагато цікавіше та корисніше, ніж про значення p.
Існує три способи вимірювання розміру ефекту залежно від типу аналізу, який ви виконуєте:
1. Стандартизована різниця середніх
Якщо ви хочете вивчити середню різницю між двома групами, відповідним способом обчислення розміру ефекту є використання стандартизованої середньої різниці . Найпопулярніша формула для використання відома як d Коена, яка обчислюється таким чином:
D Коена = ( x1 – x2 )/ с
де x 1 і x 2 — вибіркові середні значення для групи 1 і групи 2 відповідно, а s — стандартне відхилення генеральної сукупності, з якої були відібрані дві групи.
Використовуючи цю формулу, розмір ефекту легко інтерпретувати:
- d = 1 означає, що середні значення двох груп відрізняються на одне стандартне відхилення.
- d = 2 означає, що групові середні відрізняються на два стандартних відхилення.
- d = 2,5 означає, що два середні значення відрізняються на 2,5 стандартних відхилення тощо.
Інший спосіб інтерпретації розміру ефекту: розмір ефекту 0,3 означає, що оцінка середньої особи у Групі 2 на 0,3 стандартних відхилень вище середнього показника для людини в групі 1 і, отже, перевищує показники на 62% у групі 1 . .
У наведеній нижче таблиці показано різні розміри ефектів і відповідні їм процентилі:
| Розмір ефекту | Відсоток групи 2 , який був би нижчим за середній показник людей у групі 1 |
|---|---|
| 0,0 | 50% |
| 0,2 | 58% |
| 0,4 | 66% |
| 0,6 | 73% |
| 0,8 | 79% |
| 1.0 | 84% |
| 1.2 | 88% |
| 1.4 | 92% |
| 1.6 | 95% |
| 1.8 | 96% |
| 2.0 | 98% |
| 2.5 | 99% |
| 3.0 | 99,9% |
Чим більший розмір ефекту, тим більша різниця між середнім індивідуумом у кожній групі.
Загалом, d 0,2 або менше вважається малим розміром ефекту, d приблизно 0,5 вважається середнім розміром ефекту, а d 0,8 або більше вважається великим ефектом.
Таким чином, якщо середні значення двох груп не відрізняються принаймні на 0,2 стандартних відхилень, різниця є незначущою, навіть якщо p-значення є статистично значущим.
2. Коефіцієнт кореляції
Якщо ви хочете вивчити кількісний зв’язок між двома змінними, найпоширенішим способом обчислення розміру ефекту є використання коефіцієнта кореляції Пірсона . Це міра лінійного зв’язку між двома змінними X і Y. Вона має значення від -1 до 1, де:
- -1 вказує на абсолютно негативну лінійну кореляцію між двома змінними
- 0 означає відсутність лінійної кореляції між двома змінними
- 1 вказує на абсолютно позитивну лінійну кореляцію між двома змінними
Формула для розрахунку коефіцієнта кореляції Пірсона досить складна, але для тих, хто цікавиться, її можна знайти тут .
Чим далі коефіцієнт кореляції від нуля, тим сильніший лінійний зв’язок між двома змінними. Це також можна побачити, створивши просту діаграму розсіювання значень змінних X і Y.
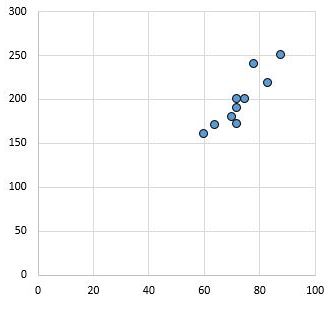
Наприклад, наступна діаграма розсіювання показує значення двох змінних з коефіцієнтом кореляції r = 0,94.
Це значення далеке від нуля, що вказує на наявність сильного позитивного зв’язку між двома змінними.
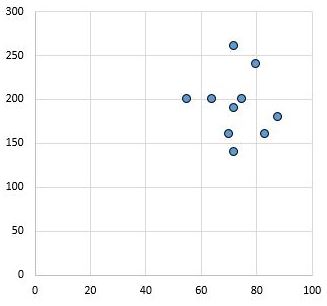
І навпаки, наступна діаграма розсіювання показує значення двох змінних, які мають коефіцієнт кореляції r = 0,03. Це значення близьке до нуля, що вказує на те, що між двома змінними практично немає зв’язку.
Загалом розмір ефекту вважається малим, якщо значення коефіцієнта кореляції Пірсона r становить приблизно 0,1, середнім, якщо r становить приблизно 0,3, і великим, якщо r дорівнює або перевищує 0,5.
3. Співвідношення шансів
Якщо ви хочете вивчити шанси на успіх у групі лікування порівняно з шансами на успіх у контрольній групі, найпоширенішим способом обчислення розміру ефекту є використання співвідношення шансів .
Наприклад, припустимо, що ми маємо таку таблицю:
| Розмір ефекту | #Успіх | #Шахи |
|---|---|---|
| Лікувальна група | МАЄ | Б |
| Контрольна група | ПРОТИ | Д |
Співвідношення шансів буде розраховано таким чином:
Співвідношення шансів = (AD) / (BC)
Чим далі співвідношення шансів від 1, тим вище ймовірність того, що лікування дасть реальний ефект.
Переваги використання розмірів ефекту над P-значеннями
Розміри ефекту мають кілька переваг перед p-значеннями:
1. Розмір ефекту допомагає нам краще зрозуміти, наскільки велика різниця між двома групами або наскільки сильний зв’язок між двома групами. P-значення може лише сказати нам, чи існує значна різниця чи значний зв’язок.
2. На відміну від p-значень, розмір ефекту можна використовувати для кількісного порівняння результатів різних досліджень, проведених у різних умовах. З цієї причини розмір ефекту часто використовується в мета-аналізі.
3. На значення P можуть впливати великі розміри вибірки. Чим більший розмір вибірки, тим більша статистична потужність перевірки гіпотези, що дозволяє виявити навіть незначні ефекти. Це може призвести до низьких значень p, незважаючи на малі розміри ефекту, які можуть не мати практичного значення.
Простий приклад може це чітко проілюструвати: припустімо, ми хочемо знати, чи дві методики дослідження призводять до різних результатів тестів. У нас є група з 20 студентів, які використовують одну техніку навчання, а інша група з 20 студентів використовує іншу техніку навчання. Потім ми даємо кожному студенту той самий тест.
Середній бал 1 групи 90,65 , 2 групи 90,75 . Стандартне відхилення для зразка 1 становить 2,77 , а стандартне відхилення для зразка 2 становить 2,78 .
Коли ми виконуємо незалежний t-тест із двома вибірками, виявляється, що статистика тесту становить -0,113 , а відповідне значення p — 0,91 . Різниця між середніми тестовими балами не є статистично значущою.
Однак подумайте, якщо розміри двох вибірок обидва були 200 , але середні значення та стандартні відхилення залишалися абсолютно однаковими.
У цьому випадку незалежний двовибірковий t-критерій показав би, що тестова статистика становить -1,97 , а відповідне значення p трохи нижче 0,05 . Різниця між середніми тестовими балами є статистично значущою.
Основна причина, чому великі розміри вибірки можуть призвести до статистично значущих висновків, пов’язана з формулою, яка використовується для обчислення статистики t- критерію:
тестова статистика t = [ ( x 1 – x 2 ) – d ] / (√ s 2 1 / n 1 + s 2 2 / n 2 )
Зверніть увагу, що коли n 1 і n 2 малі, цілочисельний знаменник статистики t -критерію є малим. А коли ділиш на мале число, то отримуєш велике число. Це означає, що статистика t- критерію буде великою, а відповідне значення p – малим, що призведе до статистично значущих результатів.
Що вважається хорошим розміром ефекту?
Питання, яке студенти часто задають: що вважається хорошим розміром ефекту?
Коротка відповідь: розмір ефекту не може бути «хорошим» чи «поганим», оскільки він просто вимірює розмір різниці між двома групами або силу асоціації між двома групами.
Однак ми можемо використовувати такі емпіричні правила, щоб кількісно визначити, чи є величина ефекту малою, середньою чи великою:
Коен Д:
- D 0,2 або менше вважається малим розміром ефекту.
- A d 0,5 вважається середнім розміром ефекту.
- Величина d 0,8 або більше вважається великим ефектом.
Коефіцієнт кореляції Пірсона
- Абсолютне значення r близько 0,1 вважається малим розміром ефекту.
- Абсолютне значення r близько 0,3 вважається середнім розміром ефекту.
- Абсолютне значення r більше 0,5 вважається великим ефектом.
Однак визначення «сильної» кореляції може відрізнятися від однієї області до іншої. Зверніться до цієї статті , щоб краще зрозуміти, що вважається сильною кореляцією між різними галузями.