Чи може z-score бути негативним?
У статистиці z-показник говорить нам, скільки стандартних відхилень має значення від середнього . Ми використовуємо наступну формулу для розрахунку z-показника:
z = (X – μ) / σ
де X – значення, яке ми аналізуємо, μ – середнє значення, а σ – стандартне відхилення.
Оцінка z може бути позитивною, негативною або нульовою.
Позитивна z-оцінка вказує на те, що певне значення вище середнього, негативна z-оцінка вказує на те, що певне значення нижче середнього, а az-оцінка нуль вказує на те, що певне значення дорівнює середньому.
Кілька прикладів повинні прояснити це.
Приклади: обчислення Z-оцінки
Скажімо, у нас є такий набір даних, який показує висоту (у дюймах) певної групи рослин:
5, 7, 7, 8, 9, 10, 13, 17, 17, 18, 19, 19, 20
Вибіркове середнє для цього набору даних становить 13 , а вибіркове стандартне відхилення – 5,51 .
1. Знайдіть z-показник для значення «8» у цьому наборі даних.
Ось як обчислити z-показник:
z = (X – μ) / σ = (8 – 13) / 5,51 = -0,91
Це означає, що значення «8» на 0,91 стандартного відхилення нижче середнього.
2. Знайдіть z-показник для значення «13» у цьому наборі даних.
Ось як обчислити z-показник:
z = (X – μ) / σ = (13 – 13) / 5,46 = 0
Це означає, що значення «13» точно дорівнює середньому.
3. Знайдіть z-показник для значення «20» у цьому наборі даних.
Ось як обчислити z-показник:
z = (X – μ) / σ = (20 – 13) / 5,46 = 1,28
Це означає, що значення «20» на 1,28 стандартних відхилень вище середнього.
Як інтерпретувати Z бали
Діаграма AZ повідомляє нам, який відсоток значень падає нижче певних Z балів. Кілька прикладів повинні прояснити це.
Приклад 1: негативні Z бали
Раніше ми виявили, що вихідне значення «8» у нашому наборі даних мало z-показник -0,91 . Згідно з таблицею Z, 18,14% значень нижче цього значення.
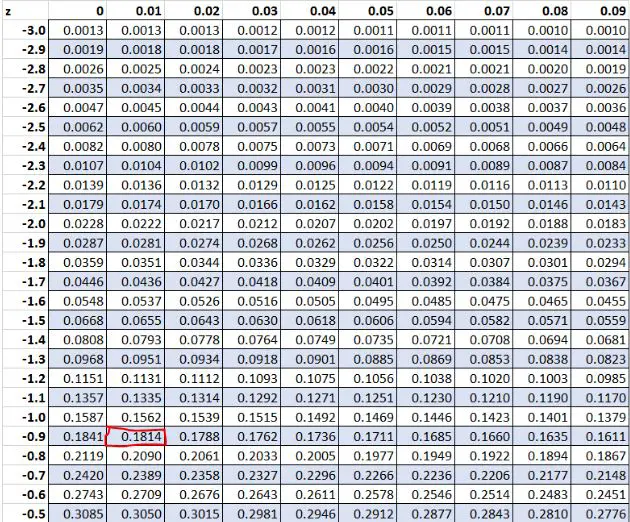
Приклад 2: Z-оцінки дорівнюють нулю
Раніше ми виявили, що необроблене значення «13» у нашому наборі даних мало z-показник 0 . Відповідно до таблиці Z, 50,00% значень менше цього значення.
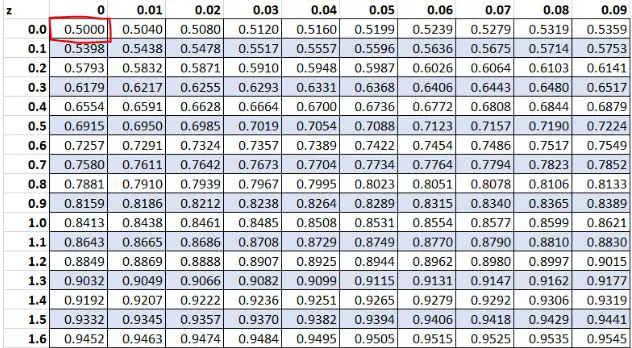
Приклад 3: Позитивні Z бали
Раніше ми виявили, що вихідне значення «20» у нашому наборі даних мало z-показник 1,28 . Згідно з таблицею Z, 89,97% значень нижче цього значення.
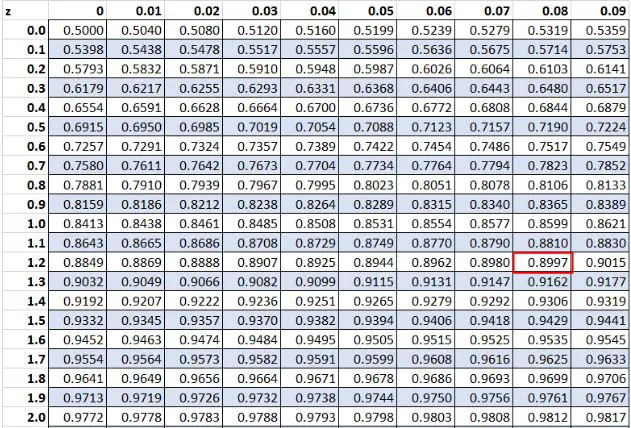
Висновок
Z-оцінки можуть мати будь-яке значення від негативної нескінченності до позитивної нескінченності, але більшість z-оцінок знаходяться в межах 2 стандартних відхилень від середнього. Насправді в статистиці існує правило, відоме як емпіричне правило , яке стверджує, що для даного набору даних із нормальним розподілом:
- 68% значень даних знаходяться в межах одного стандартного відхилення від середнього.
- 95% значень даних знаходяться в межах двох стандартних відхилень від середнього.
- 99,7% значень даних знаходяться в межах трьох стандартних відхилень від середнього.
Чим вище абсолютне значення z-показника, тим далі вихідне значення від середнього набору даних. Чим нижче абсолютне значення z-показника, тим ближче вихідне значення до середнього значення набору даних.
Пов’язані теми:
Правила калькулятора
Як застосувати емпіричне правило в Excel