Як виконати t-тест парних зразків у excel

Т-критерій для парних вибірок використовується для порівняння середніх значень двох вибірок, коли кожне спостереження в одній вибірці можна пов’язати зі спостереженням в іншій вибірці.

У цьому посібнику пояснюється, як виконати t-тест парних зразків у Excel.

Як виконати t-тест парних зразків у Excel

Припустімо, ми хочемо знати, чи певний навчальний план має значний вплив на успішність студентів на певному іспиті. Щоб перевірити це, ми просимо 20 учнів у класі пройти попередній тест. Тоді ми маємо кожного зі студентів брати участь у навчальній програмі протягом двох тижнів. Потім студенти повторно складають тест подібної складності.

Щоб порівняти різницю між середніми балами за перший і другий тести, ми використовуємо t-критерій парних зразків, оскільки для кожного студента їхній бал за перший тест можна пов’язати з його балом за другий тест.

На наступному зображенні показані оцінки кожного студента до і після тестування:

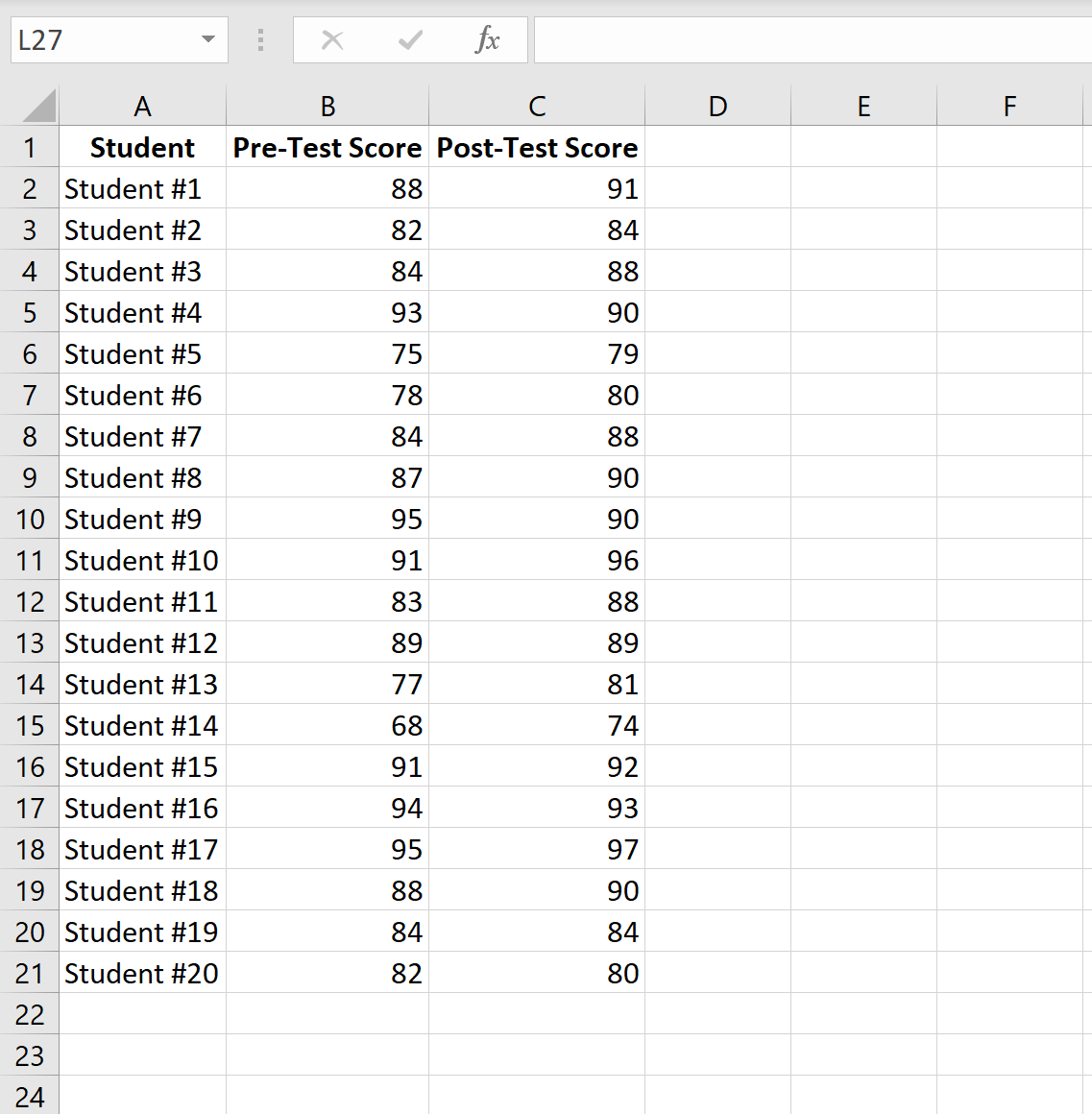
Виконайте наступні кроки, щоб виконати t-тест парних зразків, щоб визначити, чи є значна різниця в середніх результатах тесту між попереднім і посттестовим тестом.

Крок 1. Відкрийте Data Analysis ToolPak.

На вкладці «Дані» верхньої стрічки натисніть «Аналіз даних».

Якщо ви не бачите цю опцію, спершу потрібно завантажити Analysis ToolPak , який є абсолютно безкоштовним.

Крок 2: Виберіть відповідний тест для використання.

Виберіть параметр із написом T-Test: Paired Two Sample for Means і натисніть OK.

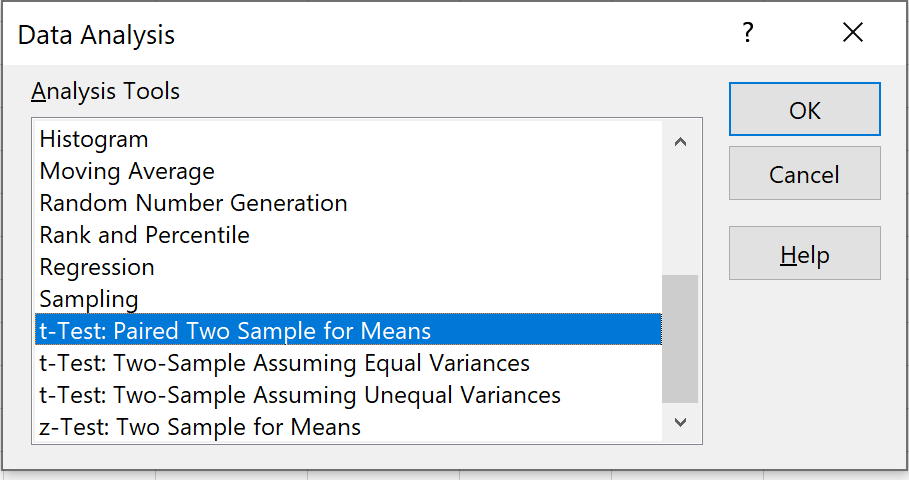
Крок 3: Введіть необхідну інформацію.

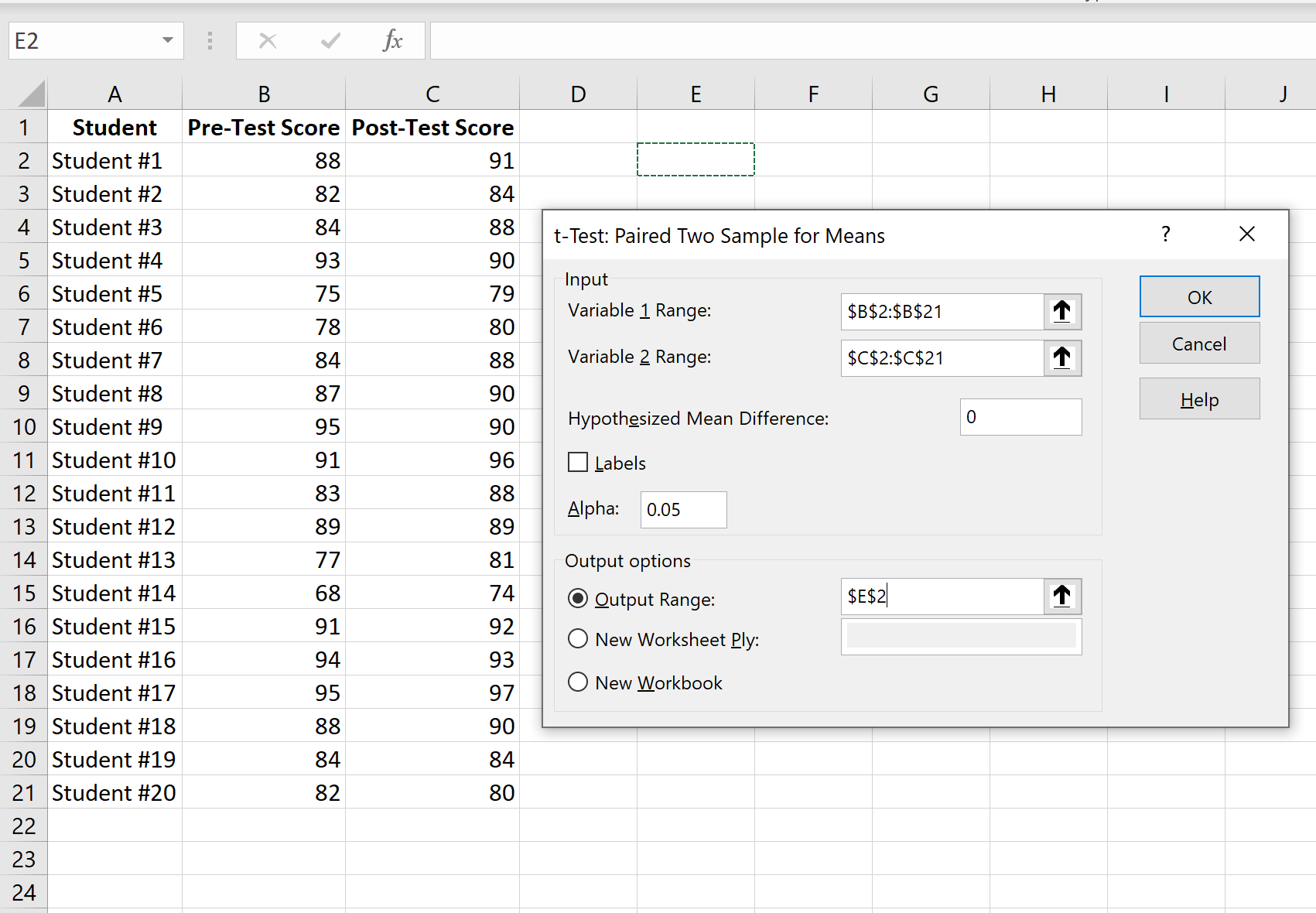
Введіть діапазон значень для змінної 1 (оцінки перед тестуванням), змінної 2 (оцінки після тестування), гіпотетичної середньої різниці (у цьому випадку ми ставимо «0», тому що ми хочемо знати, чи справжня різниця середнє значення між попередніми та післятестовими оцінками дорівнює 0), а вихідний діапазон, у якому ми хотіли б бачити результати тесту. Потім натисніть OK.

Крок 4: Інтерпретація результатів.

Після того, як ви натиснете OK на попередньому кроці, відобразяться результати t-критерію.

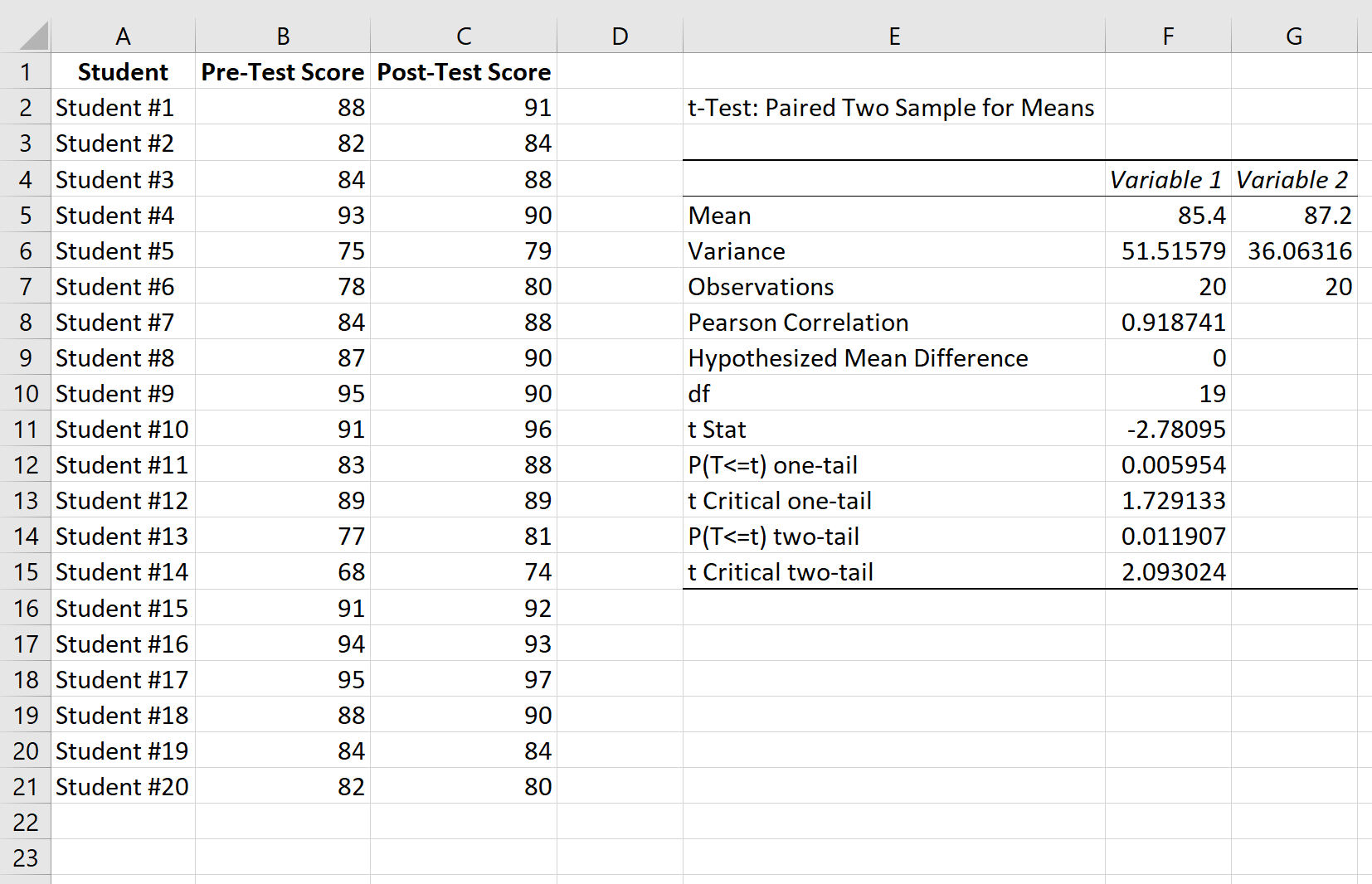
Ось як інтерпретувати результати:

Середнє: це середнє значення кожного зразка. Середній бал перед іспитом становить 85,4 , а середній бал після іспиту — 87,2 .

Дисперсія: це дисперсія для кожного зразка. Дисперсія передтестових балів становить 51,51 , а дисперсія посттестових балів – 36,06 .

Спостереження: це кількість спостережень у кожному зразку. Обидві вибірки містять по 20 спостережень.

Кореляція Пірсона: кореляція між результатами до і після тестування. Виходить 0,918 .

Гіпотетична середня різниця: число, про яке ми «висловлюємо гіпотезу», є різницею між двома середніми. У цьому випадку ми вибрали 0 , тому що ми хочемо перевірити, чи є різниця між результатами перед і після тестування.

df: Ступені свободи для t-тесту. Це обчислюється як n-1, де n – кількість пар. У цьому випадку df = 20 – 1 = 19 .

t Stat: t- критерій статистики, який дорівнює -2,78 .

Двосторонній P(T<=t): p-значення для двобічного t-тесту. У цьому випадку p = 0,011907 . Це менше, ніж альфа = 0,05, тому ми відхиляємо нульову гіпотезу. У нас є достатньо доказів, щоб стверджувати, що існує статистично значуща різниця між середнім балом до і після тесту.

t Двосторонній критичний: Це критичне значення тесту, знайдене шляхом ідентифікації значення в таблиці t-розподілу , що відповідає двосторонньому тесту з альфа = 0,05 і df = 19. Це виявляється рівним 2, 093024 . Оскільки абсолютне значення нашої t -тестової статистики більше за це значення, ми відхиляємо нульову гіпотезу. У нас є достатньо доказів, щоб стверджувати, що існує статистично значуща різниця між середнім балом до і після тесту.

Зауважте, що як підхід p-значення, так і підхід критичного значення приведуть до одного висновку.

Додаткові ресурси

У наступних посібниках пояснюється, як виконувати інші t-тести в Excel:

Як виконати t-критерій однієї вибірки в Excel
Як виконати двовибірковий t-тест у Excel