Апостеріорна ймовірність: визначення + приклад

Апостеріорна ймовірність — це оновлена ймовірність того, що подія відбудеться після врахування нової інформації.

Наприклад, нас може зацікавити ймовірність того, що подія «A» відбудеться після врахування події «B», яка щойно сталася. Ми могли б обчислити цю апостеріорну ймовірність за такою формулою:

P(A|B) = P(A) * P(B|A) / P(B)

золото:

P(A|B) = ймовірність того, що подія A відбудеться, враховуючи, що подія B відбулася. Зауважте, що «| » означає «даний».

P(A) = ймовірність того, що подія A відбудеться.

P(B) = ймовірність того, що подія B відбудеться.

P(B|A) = ймовірність того, що подія B відбудеться, враховуючи, що подія A відбулася.

Приклад: обчислення апостеріорної ймовірності

Ліс складається з 20% дубів і 80% кленів. Припустимо, ми знаємо, що 90% дубів здорові, а кленів – лише 50%. Припустимо, на відстані ви можете визначити, що конкретне дерево здорове. Яка ймовірність того, що це дерево – дуб?

Нагадаємо, що ймовірність того, що подія A відбудеться, якщо подія B відбулася, дорівнює:

P(A|B) = P(A) * P(B|A) / P(B)

У цьому прикладі ймовірність того, що дерево є дубом, якщо дерево здорове, становить:

P(Дуб|Здоровий) = P(Дуб) * P(Здоровий|Дуб) / P(Здоровий)

P(Дуб) = Ймовірність того, що дане дерево є дубом, дорівнює 0,2, оскільки 20% усіх дерев у лісі є дубами.

P(Healthy) = Імовірність того, що дане дерево є здоровим, можна розрахувати таким чином: (0,20)*(0,9) + (0,8)*(0,5) = 0,58 .

P(Healthy|Oak) = Імовірність того, що дерево здорове, якщо це дуб, дорівнює 0,9 , оскільки нам сказали, що 90% дубів здорові.

Використовуючи ці три числа, ми можемо знайти ймовірність того, що дерево є дубом, якщо воно здорове:

P(Дуб|Здоровий) = P(Дуб) * P(Здоровий|Дуб) / P(Здоровий) = (0,2) * (0,9) / (0,58) = 0,3103 .

Для інтуїтивного розуміння цієї ймовірності припустимо, що наступна сітка представляє цей ліс зі 100 дерев. Дубів рівно 20, з них 18 здорових. Інші 80 дерев – клени, з них 40 – здорові.

(O = дуб, M = клен, зелений = здоровий, червоний = нездоровий)

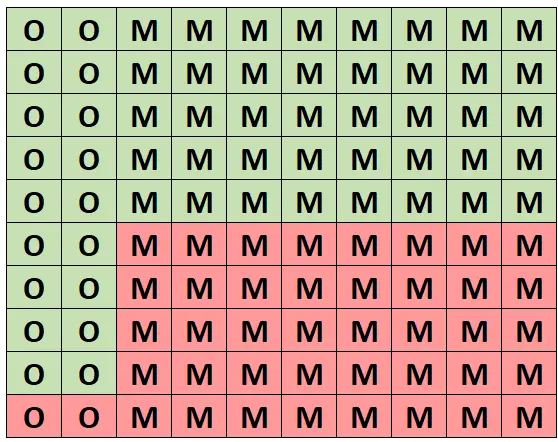
З усіх дерев рівно 58 здорових і 18 із цих здорових дерев — дуби. Отже, якщо ми знаємо, що вибрали здорове дерево, то ймовірність того, що це дуб, становить 18/58 = 0,3103 .

Коли слід використовувати апостеріорну ймовірність?

Апостеріорна ймовірність використовується в багатьох сферах, включаючи фінанси, медицину, економіку та прогноз погоди.

Сенс використання апостеріорних ймовірностей полягає в тому, щоб оновити попередні переконання, які ми мали щодо чогось, коли ми отримуємо нову інформацію.

Пригадайте з попереднього прикладу, що ми знали, що ймовірність того, що дане дерево в лісі є дубом, становить 20%. Це називається попередньою ймовірністю . Якщо ми просто виберемо дерево навмання, ми знаємо, що ймовірність того, що це буде дуб, дорівнює 0,20.

Однак, як тільки ми отримали нову інформацію про те, що вибране нами дерево було здоровим, ми змогли використати цю нову інформацію, щоб визначити, що апостериорна ймовірність того, що це дерево є дубом, натомість становила 0,3103.

У реальному світі люди постійно відкривають нову інформацію. Ця нова інформація допомагає нам оновити наші попередні переконання. У статистичних термінах це означає, що ми можемо генерувати апостеріорні ймовірності подій, які відбуваються, що допомагає нам отримати більш точне розуміння світу та дозволяє робити точніші прогнози щодо майбутніх подій.