Як виконати дисперсійний аналіз повторних вимірювань у stata

Дисперсійний аналіз із повторними вимірюваннями використовується для визначення того, чи існує статистично значуща різниця між середніми значеннями трьох або більше груп, у кожній з яких є ті самі суб’єкти.

Ми використовуємо односторонній дисперсійний аналіз повторних вимірювань у двох конкретних ситуаціях:

1. Виміряйте середні бали суб’єктів за три або більше моментів часу. Наприклад, ви можете виміряти частоту серцевих скорочень суб’єктів у спокої за місяць до початку програми тренувань, у середині програми тренувань і через місяць після програми тренувань, щоб побачити, чи є якась значна різниця в середній частоті серцевих скорочень у стані спокою. ставки за ці три моменти часу.

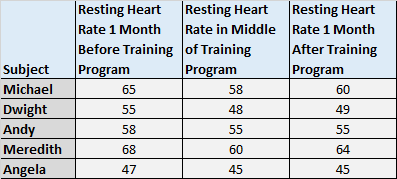
Зверніть увагу, як ті самі теми з’являються знову і знову. Ми неодноразово вимірювали тих самих суб’єктів, тому ми використовували односторонній повторний аналіз ANOVA.

2. Виміряйте середні бали суб’єктів у трьох різних умовах. Наприклад, ви можете попросити учасників переглянути три різні фільми та оцінити кожен залежно від того, наскільки вони їм сподобалися.

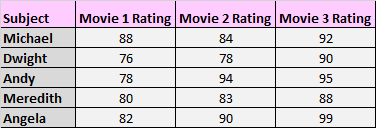
Знову ж таки, у кожній групі з’являються ті самі суб’єкти, тому ми повинні використовувати односторонній дисперсійний аналіз повторних вимірювань, щоб перевірити різницю середніх між цими трьома умовами.

У цьому підручнику пояснюється, як виконати односторонній дисперсійний аналіз повторних вимірювань у Stata.

Приклад: ANOVA повторних вимірювань у Stata

Дослідники вимірюють час реакції п’яти пацієнтів, які приймають чотири різні ліки. Оскільки кожен пацієнт вимірюється на кожному з чотирьох препаратів, ми використовуватимемо дисперсійний аналіз повторних вимірювань, щоб визначити, чи відрізняється середній час реакції між препаратами.

Виконайте наступні кроки, щоб виконати повторні вимірювання ANOVA у Stata.

Крок 1. Завантажте дані.

Спочатку завантажте дані, ввівши use https://www.stata-press.com/data/r14/t43 у полі команди та натиснувши Enter.

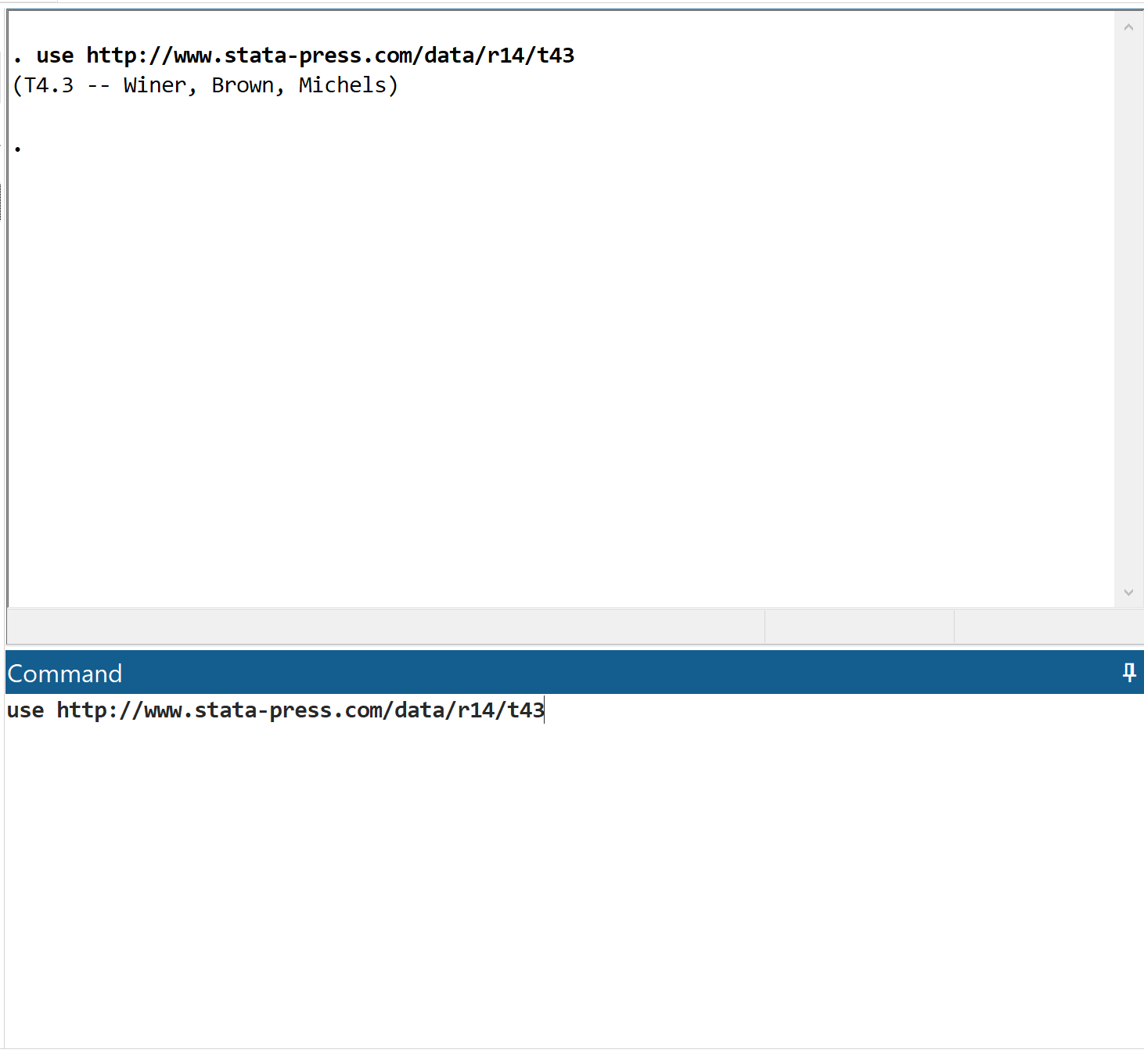
Крок 2. Перегляньте необроблені дані.

Перш ніж виконувати дисперсійний аналіз повторних вимірювань, давайте спочатку подивимося на вихідні дані. У верхній панелі меню перейдіть до Дані > Редактор даних > Редактор даних (Огляд) . Це покаже нам час відповіді для кожного з 5 пацієнтів на кожен із чотирьох препаратів:

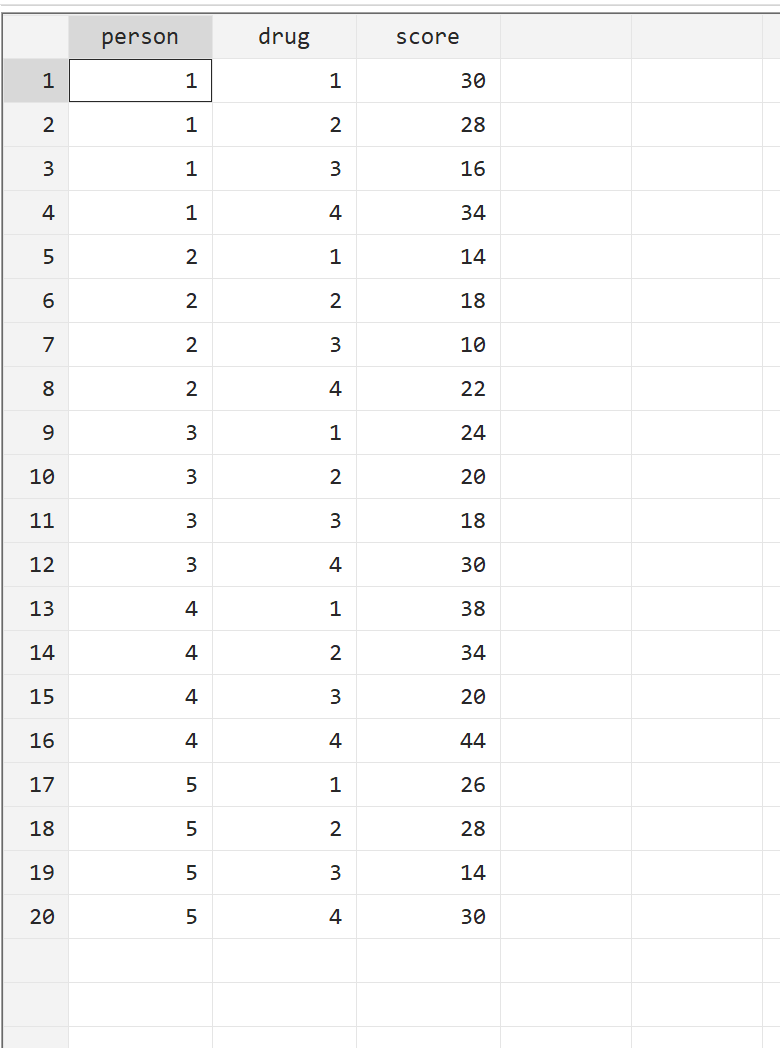
Крок 3: Виконайте повторний аналіз ANOVA.

У верхній панелі меню перейдіть до Статистика > Лінійні та пов’язані моделі > ANOVA/MANOVA > Аналіз дисперсії та коваріації .

Для залежної змінної виберіть оцінку . Для моделі виберіть людину та препарат як дві пояснювальні змінні. Поставте прапорець «Змінні повторюваних вимірювань» і виберіть препарат як змінну, яка повторюється. Залиште все, як є, і натисніть OK .

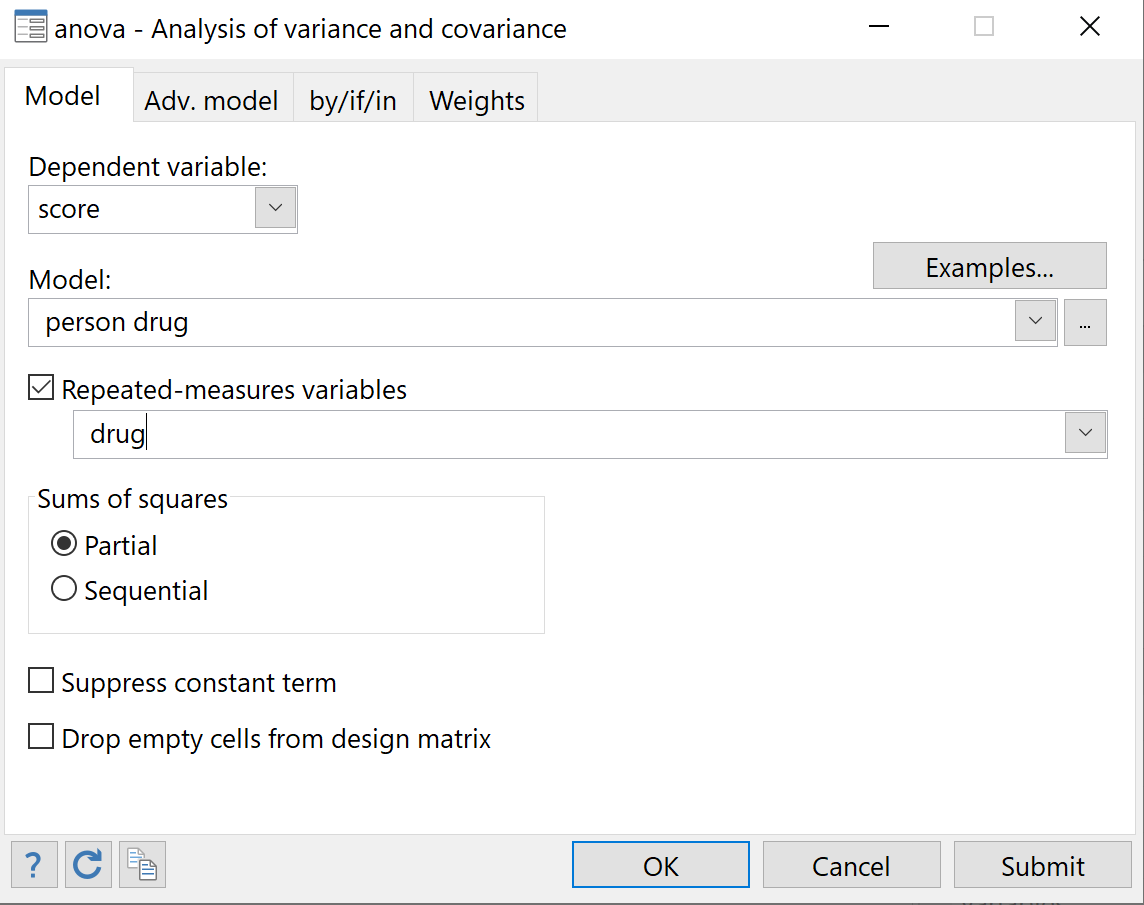
Це автоматично створить наступні дві таблиці, які показують результати повторних вимірювань ANOVA:

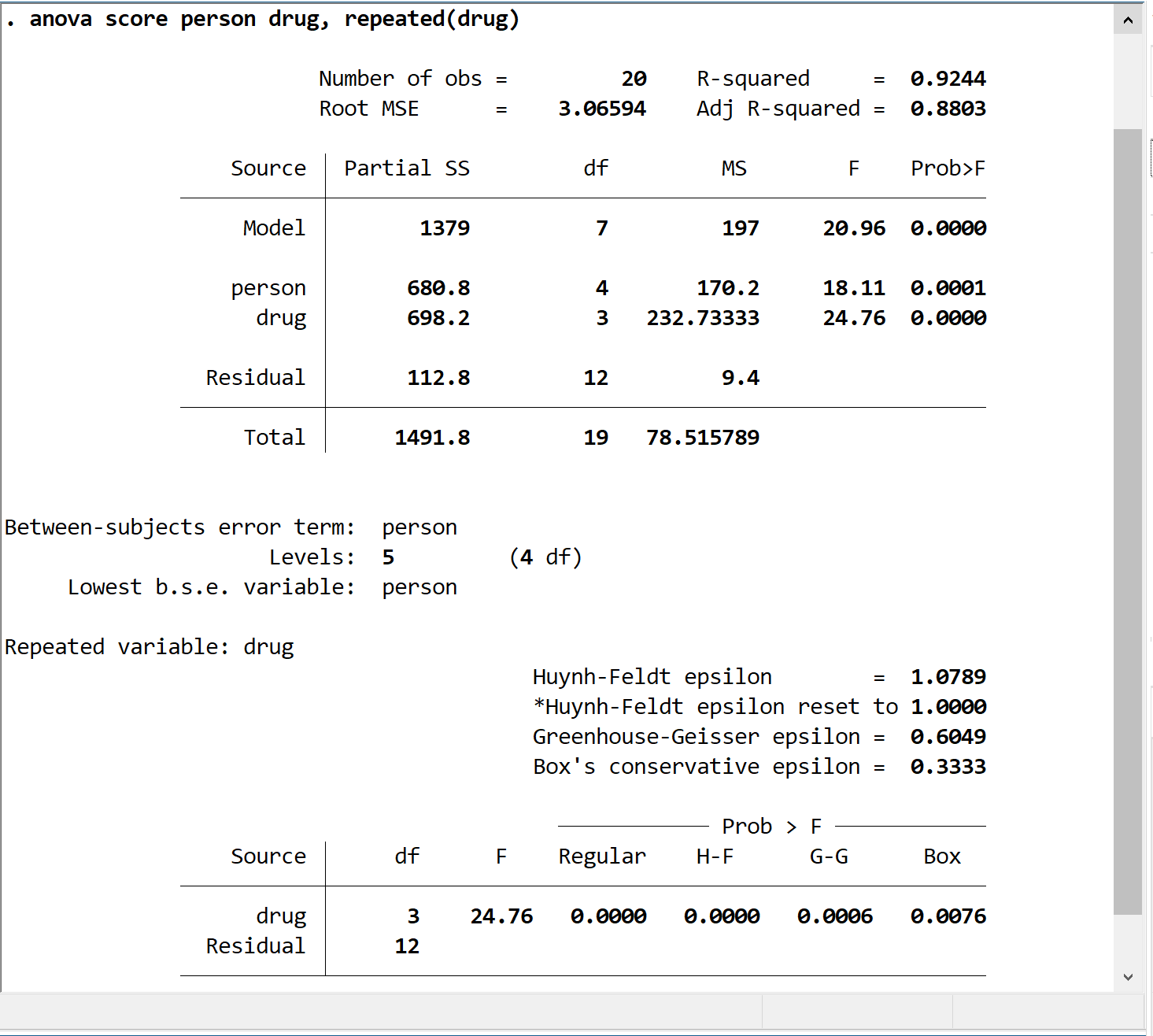
У першій таблиці нас цікавлять значення F і значення p (відображаються як Prob>F) для змінної препарату . Зверніть увагу, що F = 24,76, а p-значення становить 0,000. Це вказує на те, що існує статистично значуща різниця між середніми балами чотирьох препаратів.

Другу таблицю слід використовувати, лише якщо ми підозрюємо, що припущення про сферичність було порушено. Це припущення, що дисперсії відмінностей між усіма попарними груповими комбінаціями повинні бути рівними. Якщо ми вважаємо, що це припущення було порушено, тоді ми можемо використати один із трьох коригуючих коефіцієнтів: епсилон Хуніха-Фельдта, епсилон Гринхауса-Гейссера або консервативний епсилон Бокса.

P-значення для змінної препарату показано для кожного з цих трьох коригувальних факторів:

• p-значення Hunyh-Feldt (HF) = 0,000
• Парникове-Гейссерова (GG) р-значення = 0,0006
• Консервативне p-значення Бокса (Box) = 0,0076

Зауважте, що кожне з значень p менше 0,05, тому все ще існує статистично значуща різниця між середніми балами чотирьох препаратів, незалежно від того, який поправочний коефіцієнт ми використовуємо.

Крок 4: Повідомте про результати.

Нарешті, ми повідомимо про результати наших повторних вимірювань ANOVA. Ось приклад того, як це зробити:

Односторонній повторний аналіз ANOVA був проведений на 5 осіб, щоб дослідити вплив чотирьох різних ліків на час відповіді.

Результати показали, що тип використовуваного препарату призводив до статистично значущих відмінностей у часі відповіді (F(3, 12) = 24,75, p <0,001).