Як виконати просту лінійну регресію в stata

Проста лінійна регресія — це метод, який можна використовувати для розуміння зв’язку між пояснювальною змінною x і змінною відповіді y.

Цей посібник пояснює, як виконати просту лінійну регресію в Stata.

Приклад: проста лінійна регресія в Stata

Припустімо, ми хочемо зрозуміти зв’язок між вагою автомобіля та його милями на галон. Щоб дослідити цю залежність, ми можемо виконати просту лінійну регресію, використовуючи вагу як пояснювальну змінну та милі на галон як змінну відповіді.

Виконайте наступні кроки в Stata, щоб виконати просту лінійну регресію за допомогою набору даних під назвою auto , який містить дані про 74 різні автомобілі.

Крок 1. Завантажте дані.

Завантажте дані, ввівши наступне в полі команди:

використовуйте https://www.stata-press.com/data/r13/auto

Крок 2. Отримайте зведення даних.

Отримайте швидке розуміння даних, з якими ви працюєте, ввівши наступне в поле команди:

узагальнити

Ми бачимо, що в наборі даних є 12 різних змінних, але єдині дві, які нас цікавлять, це милі на галон і вага .

Крок 3: Візуалізуйте дані.

Перш ніж виконувати просту лінійну регресію, давайте спочатку створимо діаграму розсіювання ваги проти миль на галон, щоб ми могли візуалізувати зв’язок між цими двома змінними та перевірити наявність очевидних викидів. Щоб створити діаграму розсіювання, у полі «Команда» введіть наступне:

дисперсія ваги mpg

Це створює таку діаграму розсіювання:

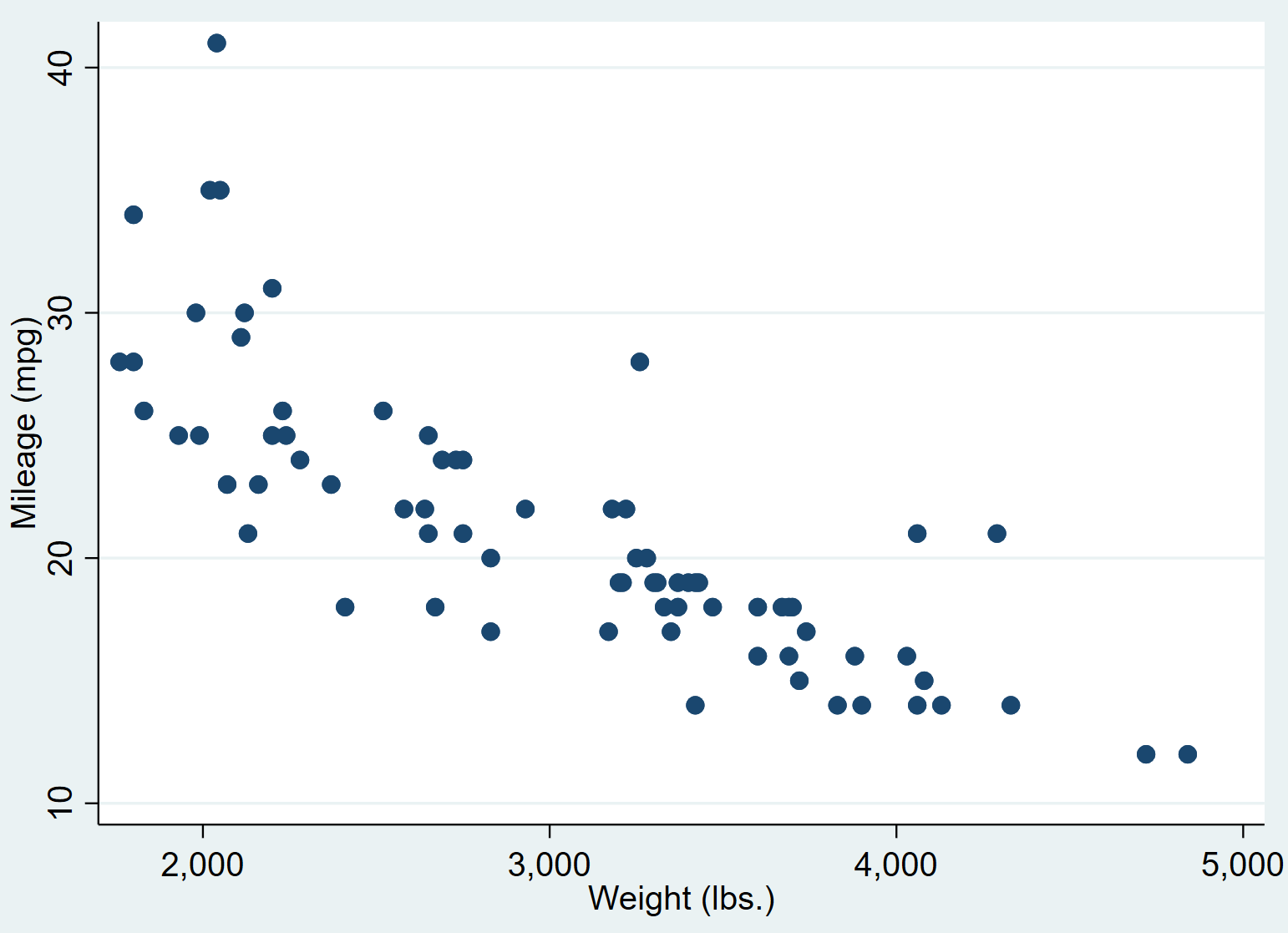
Ми бачимо, що автомобілі з більшою вагою, як правило, мають менше миль на галон. Щоб кількісно визначити цей зв’язок, ми виконаємо просту лінійну регресію.

Крок 4. Виконайте просту лінійну регресію.

Введіть наступне у полі «Команда», щоб виконати просту лінійну регресію, використовуючи вагу як пояснювальну змінну та mpg як змінну відповіді.

регрес вага до миль на галлон

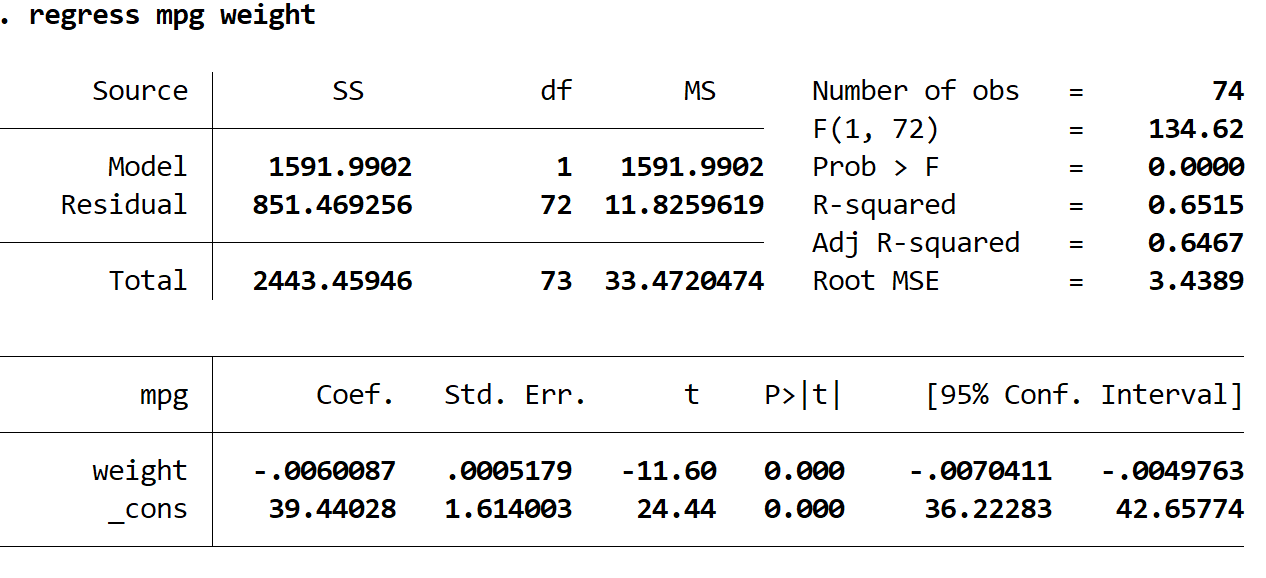
Ось як інтерпретувати найцікавіші числа в результаті:

R у квадраті: 0,6515. Це частка дисперсії у змінній відповіді, яку можна пояснити пояснювальною змінною. У цьому прикладі 65,15% варіації миль на галон можна пояснити вагою.

Коефіцієнт ваги: -0,006. Це говорить нам про середню зміну змінної відповіді, пов’язану зі збільшенням пояснювальної змінної на одиницю. У цьому прикладі кожне збільшення ваги на один фунт пов’язане зі зменшенням у середньому на 0,006 миль на галлон.

Коефіцієнт (_мінуси): 39,44028. Це говорить нам про середнє значення змінної відповіді, коли пояснювальна змінна дорівнює нулю. У цьому прикладі середня миля на галон становить 39,44028, коли вага автомобіля дорівнює нулю. Це насправді не має сенсу інтерпретувати, оскільки вага автомобіля не може дорівнювати нулю, але число 39,44028 необхідне для формування рівняння регресії.

P>|t| (вага): 0,000. Це p-значення, пов’язане зі статистикою тесту для ваги. У цьому випадку, оскільки це значення менше 0,05, ми можемо зробити висновок, що існує статистично значущий зв’язок між вагою та милями на галон.

Рівняння регресії: нарешті, ми можемо сформувати рівняння регресії, використовуючи два значення коефіцієнта. У цьому випадку рівняння буде таким:

прогнозований миль на галон = 39,44028 – 0,0060087*(вага)

Ми можемо використати це рівняння, щоб знайти очікувану кількість миль на галлон для автомобіля, враховуючи його вагу. Наприклад, автомобіль, який важить 4000 фунтів, повинен мати 15 405 миль на галон:

прогнозований миль на галон = 39,44028 – 0,0060087*(4000) = 15,405

Крок 5: Повідомте про результати.

Нарешті, ми хочемо повідомити про результати нашої простої лінійної регресії. Ось приклад того, як це зробити:

Для кількісного визначення співвідношення між вагою автомобіля та його милями на галон була проведена лінійна регресія. Для аналізу була використана вибірка з 74 автомобілів.

Результати показали, що існує статистично значущий зв’язок між вагою та милями на галон (t = -11,60, p < 0,0001), і що вага становить 65,15% поясненої варіабельності миль на галон.

Рівняння регресії вийшло таким:

прогнозований миль на галон = 39,44 – 0,006 (вага)

Кожен додатковий фунт був пов’язаний зі зниженням, в середньому, на -0,006 милі на галон.