Як використовувати надійні стандартні помилки в регресії в stata

Множинна лінійна регресія — це метод, який ми можемо використовувати для розуміння зв’язку між декількома пояснювальними змінними та змінною відповіді.

На жаль, проблема, яка часто виникає в регресії, відома як гетероскедастичність , у якій існує систематична зміна дисперсії залишків у діапазоні виміряних значень.

Це призводить до збільшення дисперсії оцінок коефіцієнта регресії, але регресійна модель не враховує це. Це значно підвищує ймовірність того, що регресійна модель стверджуватиме, що термін у моделі є статистично значущим, хоча насправді це не так.

Одним із способів пояснити цю проблему є використання надійних стандартних помилок , які є більш «стійкими» до проблеми гетероскедастичності та, як правило, забезпечують точнішу міру справжньої стандартної помилки коефіцієнта регресії.

У цьому підручнику пояснюється, як використовувати надійні стандартні помилки в регресійному аналізі в Stata.

Приклад: надійні стандартні помилки в Stata

Ми використаємо автоматично інтегрований набір даних Stata, щоб проілюструвати, як використовувати надійні стандартні помилки в регресії.

Крок 1: Завантажте та відобразіть дані.

Спочатку скористайтеся такою командою, щоб завантажити дані:

автоматичне використання системи

Потім відобразіть необроблені дані за допомогою такої команди:

бр

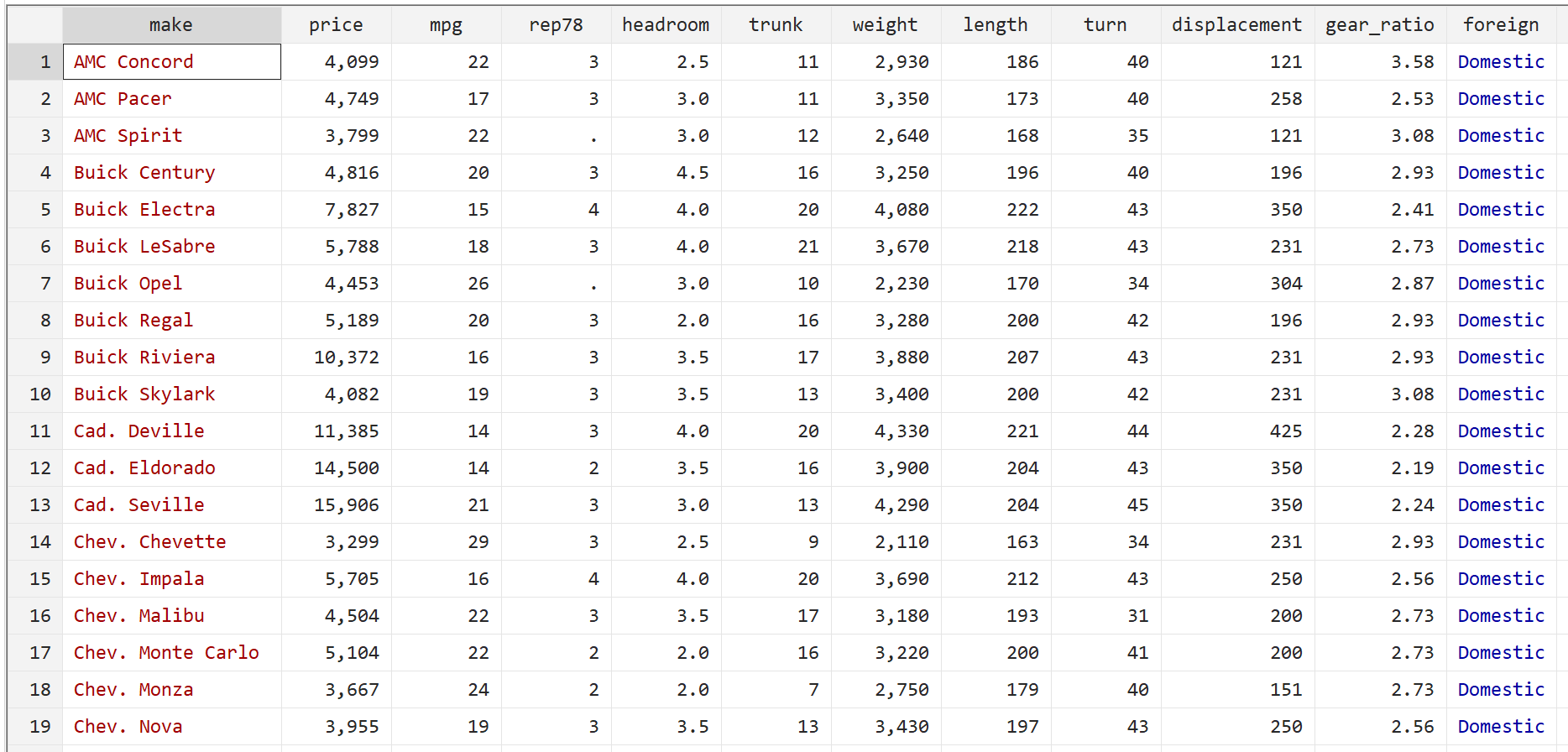
Крок 2: Виконайте множинну лінійну регресію без надійних стандартних помилок.

Далі ми введемо таку команду, щоб виконати множинну лінійну регресію, використовуючи ціну як змінну відповіді та милі на галон і вагу як пояснювальні змінні:

регресія ціна mpg вага

Крок 3: Виконайте множинну лінійну регресію, використовуючи надійні стандартні помилки.

Тепер ми виконаємо ту саму множинну лінійну регресію, але цього разу використаємо команду vce(robust) , щоб Stata знала, як використовувати надійні стандартні помилки:

регресія ціна mpg вага, vce (надійний)

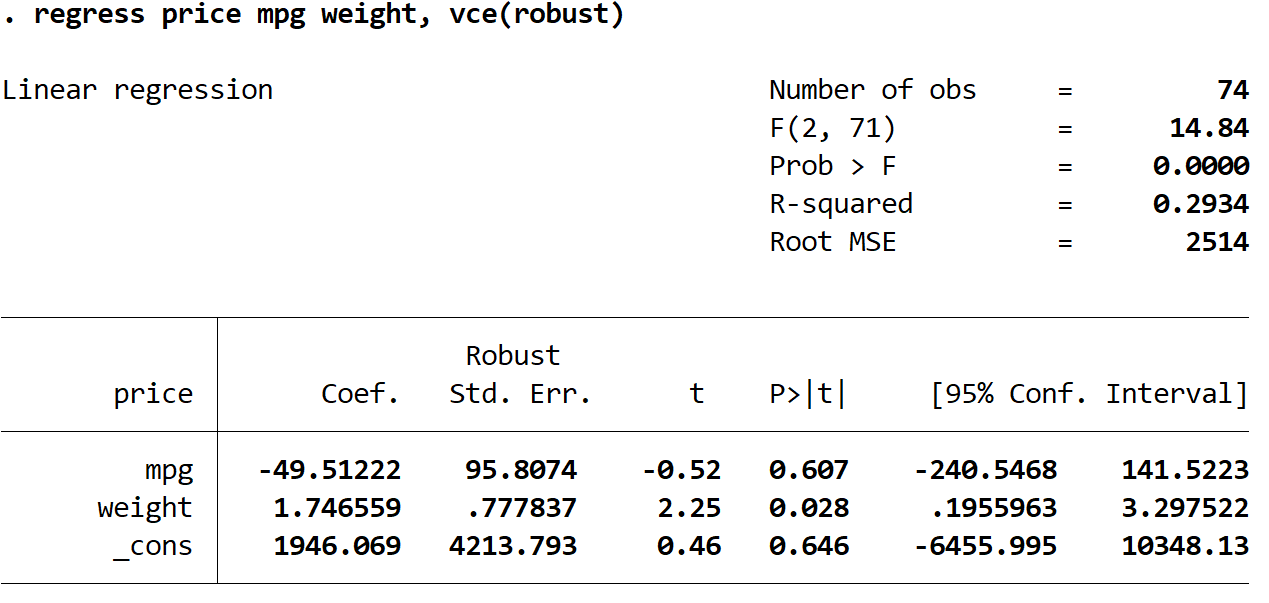
Тут варто відзначити кілька цікавих речей:

1. Коефіцієнт оцінки залишився колишнім . Коли ми використовуємо стійкі стандартні помилки, оцінки коефіцієнтів взагалі не змінюються. Зауважте, що оцінки коефіцієнтів для миль на галон, ваги та константи є такими для обох регресій:

• mpg: -49,51222
• вага: 1.746559
• _проти: 1946.069

2. Стандартні помилки змінилися . Зауважте, що коли ми використовували стійкі стандартні помилки, стандартні помилки для кожної з оцінок коефіцієнта зросли.

Примітка. У більшості випадків стійкі стандартні помилки будуть більшими, ніж звичайні стандартні помилки, але в окремих випадках можливо, що надійні стандартні помилки насправді будуть меншими.

3. Тестова статистика кожного коефіцієнта змінилася. Зверніть увагу, що абсолютне значення кожної тестової статистики , t , зменшилося. По суті, тестова статистика обчислюється як розрахунковий коефіцієнт, поділений на стандартну помилку. Таким чином, чим більше стандартна помилка, тим менше абсолютне значення тестової статистики.

4. P-значення змінилися . Зверніть увагу, що p-значення для кожної змінної також зросли. Це пояснюється тим, що менша статистика тесту пов’язана з більшими значеннями p.

Хоча значення p для наших коефіцієнтів змінилися, змінна mpg все ще не є статистично значущою при α = 0,05, а вага змінної все ще є статистично значущою при α = 0,05.