Дисперсія

за Редакція 5 Серпня, 2023 Статистика 0 коментарів

У цій статті ми пояснюємо, що таке дисперсія, яка також називається дисперсією, і як вона обчислюється. Ви знайдете формулу дисперсії, конкретний приклад обчислення дисперсії та, крім того, ви зможете розрахувати дисперсію будь-якого набору даних за допомогою онлайн-калькулятора.

Ми також покажемо вам, як знайти дисперсію згрупованих даних, оскільки це робиться іншим способом. Нарешті, ми навчимо вас різниці між дисперсією сукупності та дисперсією вибірки, різницею між дисперсією та стандартним відхиленням і властивостями цього статистичного показника.

Що таке дисперсія?

У статистиці дисперсія — це міра дисперсії, яка вказує на мінливість випадкової величини. Дисперсія дорівнює сумі квадратів залишків, поділеної на загальну кількість спостережень.

Майте на увазі, що нев’язка розуміється як різниця між значенням точки статистичних даних і середнім значенням набору даних.

У теорії ймовірностей символом дисперсії є грецька літера сигма в квадраті (σ ² ). Хоча він також зазвичай представлений як Var(X) , де X є випадковою змінною, з якої обчислюється дисперсія.

Загалом, інтерпретація значення дисперсії випадкової змінної проста. Чим більше значення дисперсії, тим більше розсіяні дані. І навпаки, чим менше значення дисперсії, тим менша дисперсія буде в ряді даних. Однак, інтерпретуючи дисперсію, слід бути обережним із викидами , оскільки вони можуть спотворити значення дисперсії.

дисперсії, іншими показниками, які вважаються крім дисперсії, є діапазон, стандартне відхилення, середнє відхилення та коефіцієнт варіації.

Як розрахувати розрив

Щоб розрахувати дисперсію, необхідно виконати наступні кроки:

Знайдіть середнє арифметичне набору даних.
Обчисліть залишки, визначені як різниця між значеннями та середнім значенням набору даних.
Зведіть кожен залишок у квадрат.
Додайте всі результати, обчислені на попередньому кроці.
Розділіть на загальну кількість даних. Отриманий результат є дисперсією ряду даних.

Підсумовуючи, формула для обчислення дисперсії набору даних виглядає так:

золото:

$X$

це випадкова змінна, для якої потрібно обчислити дисперсію.
$x_i$

це значення даних

$i$

.
$n$

– загальна кількість спостережень.
$\overline{X}$

є середнім значенням випадкової величини

$X$

.

👉 Ви можете скористатися калькулятором нижче, щоб обчислити дисперсію будь-якого набору даних.

Тому, щоб отримати дисперсію з ряду даних, важливо знати, як обчислюється середнє арифметичне. Якщо ви не пам’ятаєте, як це зробити, ви можете перевірити це в статті, за посиланням вище.

Приклад відхилення

Тепер, коли ми знаємо визначення дисперсії, ми крок за кроком вирішимо вправу, щоб ви могли побачити, як виходить дисперсія ряду даних.

З транснаціональної компанії відомий економічний результат, який вона мала за останні п’ять років, здебільшого вона отримала прибуток, але за один рік вона представила значні збитки: 11,5, 2, -9, 7 мільйонів євро. Обчисліть дисперсію цього набору даних.

Як ми бачили в поясненні вище, перше, що нам потрібно зробити, щоб знайти дисперсію ряду даних, це обчислити його середнє арифметичне:

$\overline{X}=\cfrac{11+5+2+(-9)+7}{5}=3,2$

І коли ми знаємо середнє значення даних, ми можемо використовувати формулу дисперсії:

$Var(X)=\cfrac{\displaystyle\sum_{i=1}^n\left(x_i-\overline{X}\right)^2}{n}$

Підставляємо дані, надані оператором вправи, у формулу:

$Var(X)=\cfrac{\displaystyle (11-3,2)^2+(5-3,2)^2+(2-3,2)^2+(-9-3,2)^2+(7-3,2)^2}{5}$

Нарешті, все, що залишилося, це вирішити операції для обчислення дисперсії:

$\begin{aligned}Var(X)&=\cfrac{7,8^2+1,8^2+(-1,2)^2+(-12,2)^2+3,8^2}{5}\\[2ex]&=\cfrac{60,84+3,24+1,44+148,84+14,44}{5}\\[2ex]&= \cfrac{228,8}{5} \\[2ex]&=45,76 \ \text{millones de euros}^2\end{aligned}$

Зверніть увагу, що одиниці дисперсії є тими самими одиницями статистичних даних, але зведені в квадрат, тому дисперсія цієї групи даних становить 45,76 мільйонів євро ² .

Калькулятор розриву

Введіть набір статистичних даних у наступний калькулятор, щоб обчислити його дисперсію. Дані повинні бути розділені пробілом і введені крапкою як десятковим роздільником.

Дисперсія для згрупованих даних

Щоб обчислити дисперсію даних, згрупованих в інтервали , потрібно виконати наступні кроки:

Знайдіть середнє значення згрупованих даних.
Обчисліть залишки згрупованих даних.
Зведіть кожен залишок у квадрат.
Помножте кожен попередній результат на частоту його інтервалу.
Складіть суму всіх значень, отриманих на попередньому кроці.
Розділіть на загальну кількість спостережень. Отримане число є дисперсією згрупованих даних.

Іншими словами, формула для обчислення дисперсії даних, згрупованих в інтервали, виглядає наступним чином:

$Var(X)=\cfrac{\displaystyle\sum_{i=1}^n\left(x_i-\overline{X}\right)^2\cdot f_i }{n}$

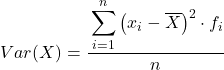
Хоча зазвичай використовується наведена вище формула, алгебраїчний вираз, наведений нижче, також можна використовувати, оскільки він еквівалентний:

$Var(X)=\cfrac{\displaystyle\sum_{i=1}^n x_i^2\cdot f_i }{n}-\overline{X}^2$

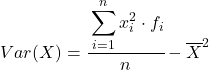
Як приклад, ми знайдемо дисперсію наступного згрупованого ряду даних:

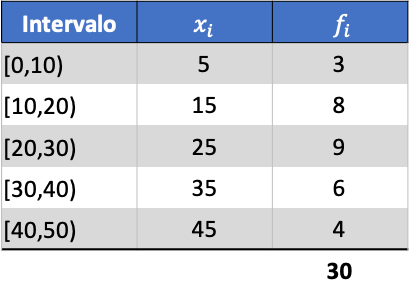
Спочатку нам потрібно визначити середнє значення згрупованих даних. Для цього додаємо в таблицю частот стовпець з добутком позначки класу на частоту:

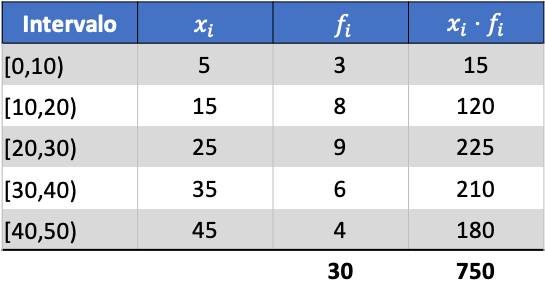
Тепер ми обчислюємо середнє значення згрупованих даних, розділивши суму доданого стовпця на загальну кількість даних:

$\overline{X}=\cfrac{\displaystyle\sum_{i=1}^n x_i\cdot f_i}{n}=\cfrac{750}{30}=25$

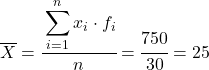
І з середнього значення обчислених даних ми можемо додати наступні три стовпці:

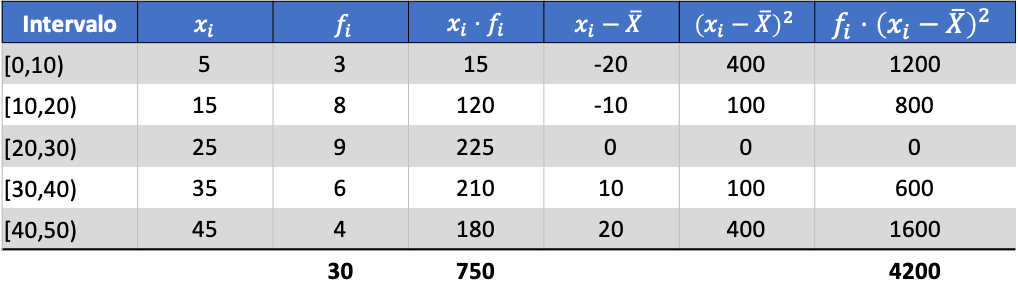
Отже, дисперсія об’єднаного набору даних – це сума останнього стовпця, поділена на загальну кількість спостережуваних даних:

$Var(X)=\cfrac{\displaystyle\sum_{i=1}^n\left(x_i-\overline{X}\right)^2\cdot f_i }{n}=\cfrac{4200}{30}=140$

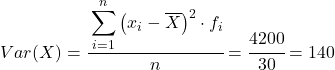
Дисперсія і стандартне відхилення

Дисперсія та стандартне відхилення (або стандартне відхилення) є двома мірами дисперсії, тому обидва вказують на ступінь дисперсії набору даних. Однак різниця між дисперсією та стандартним відхиленням полягає в тому, що загалом дисперсія має більші значення, оскільки вона є квадратом стандартного відхилення.

Стандартне відхилення зазвичай позначається грецькою літерою сигма (σ), і з цієї причини дисперсія представлена літерою сигма в квадраті (σ ² ), оскільки це математичний зв’язок, який існує між цими двома метриками дисперсії.

$Var(X)=\sigma^2$

Отже, коли ви обчислили значення дисперсії набору даних, ви можете легко знайти значення стандартного відхилення того самого набору, просто взявши квадратний корінь з дисперсії.

$\sigma=\sqrt{\sigma^2}$

Дисперсія сукупності та дисперсія вибірки

Логічно, дисперсія генеральної сукупності відноситься до розрахунку дисперсії статистичної генеральної сукупності, а замість цього дисперсія вибірки застосовується до розрахунку дисперсії вибірки. Однак це дві різні концепції, оскільки формула дисперсії сукупності відрізняється від формули дисперсії вибірки.

Зазвичай у вправах на дисперсію, якщо вони не говорять нам про інше, щоб знайти дисперсію наданого набору даних, ми повинні використовувати формулу дисперсії генеральної сукупності , яку ми пояснювали на початку статті:

$\sigma^2=\cfrac{\displaystyle\sum_{i=1}^n\left(x_i-\overline{X}\right)^2}{n}$

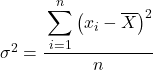
Але, можливо, у деяких задачах вас просять розглядати статистичні дані як вибірку, і в цьому випадку нам потрібно використовувати формулу дисперсії вибірки :

$s^2=\cfrac{\displaystyle\sum_{i=1}^n\left(x_i-\overline{X}\right)^2}{n-1}$

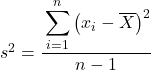
Зауважте, що для вказівки на те, що дисперсія генеральної сукупності обчислюється, вона позначається грецькою літерою σ, але коли дисперсія вибірки обчислюється, використовується літера s.

Як ви бачите, єдина різниця між двома формулами полягає в тому, що дисперсію вибірки нам потрібно поділити на загальну кількість спостережень мінус 1, наприклад, якщо загалом є 30 елементів даних, ми поділимо на 29 Але розрахунок чисельника проводиться точно так само.

Властивості дисперсії

Дисперсія має такі властивості:

Дисперсія будь-якої випадкової величини завжди буде більше або дорівнює нулю. Так само, якщо дисперсія дорівнює нулю, це означає, що всі статистичні дані однакові.

$Var(x)\ge 0$

Очевидно, що дисперсія одного значення дорівнює нулю.

$Var(a)=0\qquad a\in \mathbb{R}$

Дисперсія добутку скаляра на змінну еквівалентна цьому скаляру в квадраті, помноженому на дисперсію змінної.

$Var(aX)=a^2\cdot Var(X)\qquad a\in \mathbb{R}$

Дисперсія суми двох залежних змінних еквівалентна сумі дисперсії кожної змінної окремо плюс подвоєна коваріація між двома змінними.

$Var(X+Y)=Var(X)+Var(Y)+2Cov(X,Y)$

Отже, якщо дві змінні незалежні, то для визначення дисперсії їх суми достатньо скласти їх дисперсії:

$Var(X+Y)=Var(X)+Var(Y)$

Відхилення також можна визначити за допомогою математичного сподівання за такою формулою:

$Var(X)=E\bigl[(X-\overline{X})^2\bigr]$

Про автора

Редакція

Привіт, я Бенджамін, професор статистики на пенсії, який став викладачем статистики. Маючи великий досвід і знання в галузі статистики, я готовий поділитися своїми знаннями, щоб розширити можливості студентів через Statorials. Дізнайтеся більше