Як перевірити нормальність у stata

Багато статистичних тестів вимагають, щоб одна або більше змінних були нормально розподілені , щоб результати тесту були надійними.

Цей підручник пояснює кілька методів, які можна використовувати для перевірки нормальності між змінними в Stata.

Для кожного з цих методів ми будемо використовувати вбудований набір даних Stata під назвою auto . Ви можете завантажити цей набір даних за допомогою такої команди:

автоматичне використання системи

Спосіб 1: гістограми

Неофіційний спосіб перевірити, чи змінна розподілена нормально, — створити гістограму для відображення розподілу змінної.

Якщо змінна має нормальний розподіл, гістограма має мати форму «дзвіночка» з більшою кількістю значень, розташованих біля центру, і меншою кількістю значень, розташованих на хвостах.

Ми можемо використати команду hist , щоб створити гістограму для змінного переміщення :

рухома історія

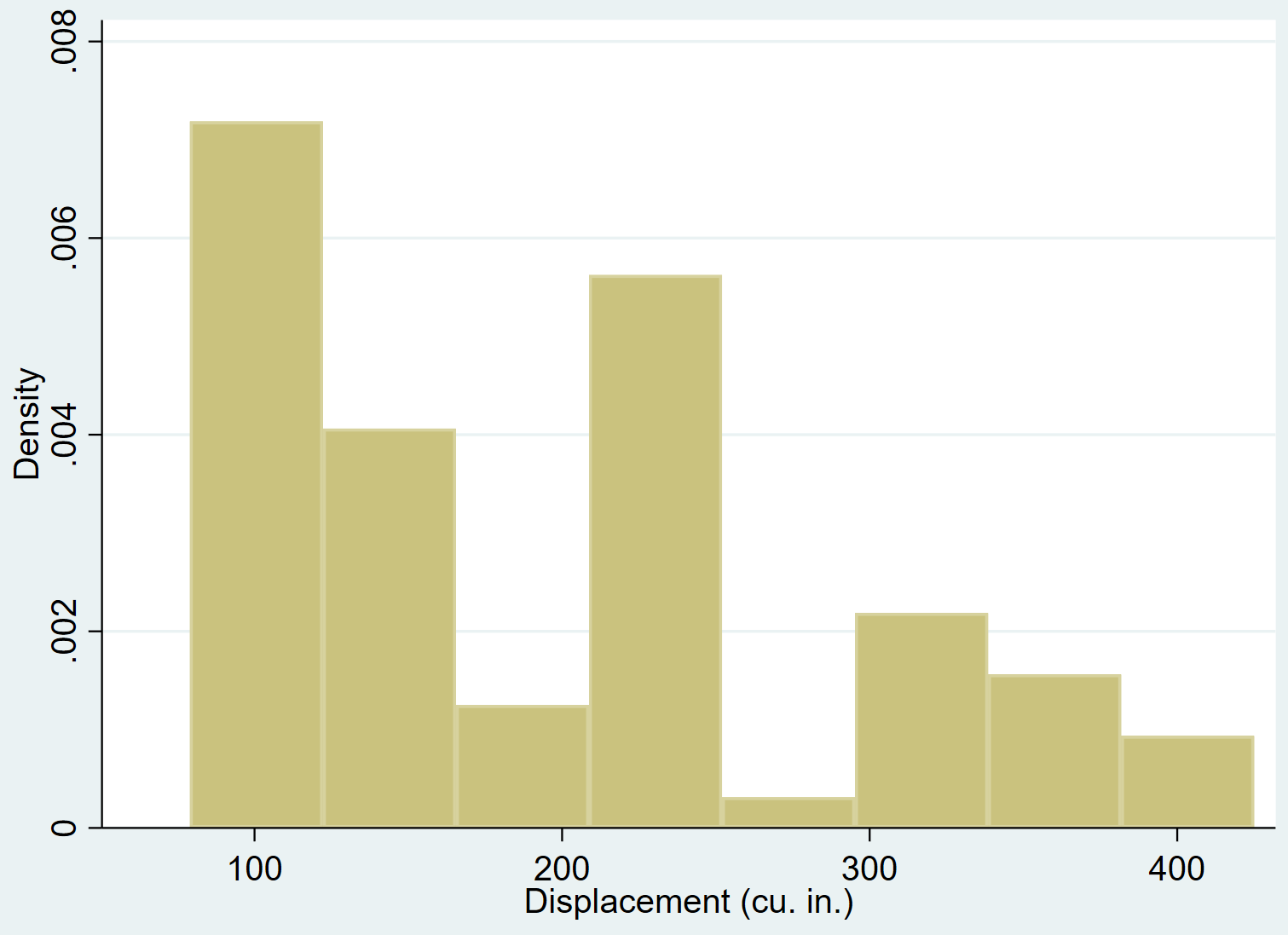
Ми можемо додати нормальну криву щільності до гістограми за допомогою команди normal :

рухома історія, нормальна

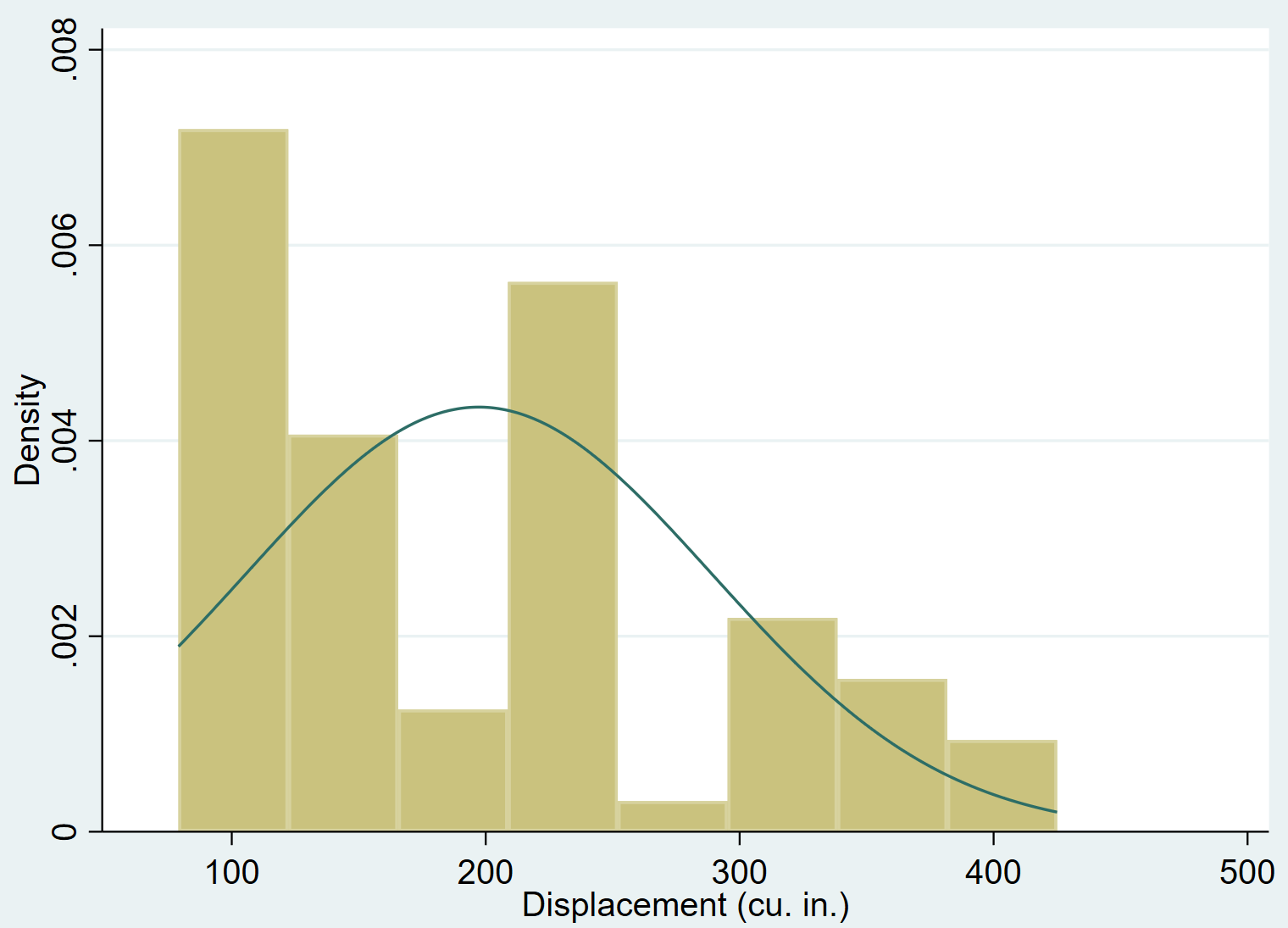
Цілком очевидно, що зсув змінної зміщений вправо (наприклад, більшість значень зосереджено ліворуч, а довгий «хвіст» значень тягнеться праворуч) і не відповідає нормальному розподілу.

Пов’язані: лівий і правий викривлені розподіли

Метод 2: Тест Шапіро-Вілка

Формальним способом перевірки нормальності є використання тесту Шапіро-Вілка .

Нульова гіпотеза для цього тесту полягає в тому, що змінна має нормальний розподіл. Якщо p-значення тесту нижче певного рівня значущості (загальні варіанти включають 0,01, 0,05 і 0,10), тоді ми можемо відхилити нульову гіпотезу та зробити висновок, що є достатньо доказів, щоб стверджувати, що змінна не розподілена нормально .

*Цей тест можна використовувати, якщо загальна кількість спостережень становить від 4 до 2000.

Ми можемо використовувати команду swilk , щоб виконати тест Шапіро-Вілка на змінному об’ємі :

плавний рух

Ось як інтерпретувати результат тесту:

Спостереження: 74. Це кількість спостережень, використаних у тесті.

W: 0,92542. Це тестова статистика для тесту.

Prob>z: 0,00031. Це p-значення, пов’язане з тестовою статистикою.

Оскільки p-значення менше 0,05, ми можемо відхилити нульову гіпотезу тесту. Ми маємо достатньо доказів, щоб стверджувати, що змінне зміщення не розподілене нормально.

Ми також можемо виконати тест Шапіро-Вілка для кількох змінних одночасно, перерахувавши кілька змінних після команди swilk :

swilk переміщення mpg довжина

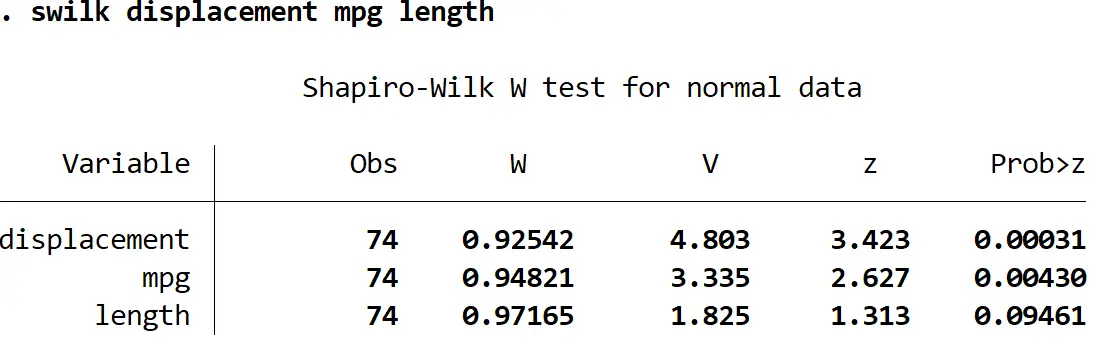
Використовуючи рівень значущості 0,05, ми зробили б висновок, що об’єм і миль на галлон не розподіляються нормально, але ми не маємо достатньо доказів, щоб стверджувати, що довжина розподілена ненормально.

Спосіб 3: Тест Шапіро-Франчіа

Іншим офіційним способом перевірки нормальності є використання тесту Шапіро-Франчіа .

Нульова гіпотеза для цього тесту полягає в тому, що змінна має нормальний розподіл. Якщо p-значення тесту нижче певного рівня значущості, тоді ми можемо відхилити нульову гіпотезу та зробити висновок, що є достатньо доказів того, що змінна не розподілена нормально.

*Цей тест можна використовувати, якщо загальна кількість спостережень становить від 10 до 5000.

Ми можемо використати команду sfrancia для виконання тесту Шапіро-Вілка на змінному об’ємі :

переміщення sfrancia

Ось як інтерпретувати результат тесту:

Спостереження: 74. Це кількість спостережень, використаних у тесті.

W’: 0,93011. Це тестова статистика для тесту.

Prob>z: 0,00094. Це p-значення, пов’язане з тестовою статистикою.

Оскільки p-значення менше 0,05, ми можемо відхилити нульову гіпотезу тесту. Ми маємо достатньо доказів, щоб стверджувати, що змінне зміщення не розподілене нормально.

Подібно до тесту Шапіро-Вілка, ви можете виконати тест Шапіро-Франчіа для кількох змінних одночасно, перерахувавши кілька змінних після команди sfrancia .

Метод 4: перевірка асиметрії та ексцесу

Іншим способом перевірки нормальності є використання тесту асиметрії та ексцесу , який визначає, чи відповідають асиметрія та ексцес змінної нормальному розподілу.

Нульова гіпотеза для цього тесту полягає в тому, що змінна має нормальний розподіл. Якщо p-значення тесту нижче певного рівня значущості, тоді ми можемо відхилити нульову гіпотезу та зробити висновок, що є достатньо доказів того, що змінна не розподілена нормально.

*Цей тест вимагає мінімум 8 спостережень.

Ми можемо використати команду sktest , щоб виконати тест на асимметрию та ексцесс для змінного переміщення :

переміщення тесту

Ось як інтерпретувати результат тесту:

Спостереження: 74. Це кількість спостережень, використаних у тесті.

adj chi(2): 5,81. Це статистика тесту хі-квадрат для тесту.

Prob>chi2: 0,0547. Це p-значення, пов’язане з тестовою статистикою.

Оскільки p-значення не менше 0,05, ми не можемо відхилити нульову гіпотезу тесту. У нас недостатньо доказів, щоб стверджувати, що рухи не розподіляються нормально.

Подібно до інших тестів на нормальність, ви можете виконати тест асиметрії та ексцесу для кількох змінних одночасно, перерахувавши кілька змінних після команди sktest .