Як виконати u-тест манна-уітні в excel

Критерій Манна-Уїтні U (іноді його називають тестом рангової суми Вілкоксона) використовується для порівняння відмінностей між двома вибірками, коли розподіл вибірки не є нормальним, а розміри вибірки невеликі (n < 30).

Він вважається непараметричним еквівалентом двовибіркового t-критерію .

У цьому посібнику пояснюється, як виконати U-тест Манна-Уітні в Excel.

Приклад: тест Манна-Уітні U в Excel

Дослідники хочуть знати, чи обробка палива спричиняє зміну середньої витрати миль на галлон автомобіля. Щоб перевірити це, вони проводять експеримент, під час якого вимірюють миль на галлон 12 автомобілів з обробленим паливом і 12 автомобілів без обробки.

Оскільки розмір вибірки невеликий і вони підозрюють, що розподіл вибірки не є нормальним, вони вирішили виконати U-тест Манна-Уітні, щоб визначити, чи є статистично значуща різниця в милях на галон між двома групами.

Виконайте наведені нижче дії, щоб виконати U-тест Манна-Уітні в Excel.

Крок 1: Введіть дані.

Введіть дані наступним чином:

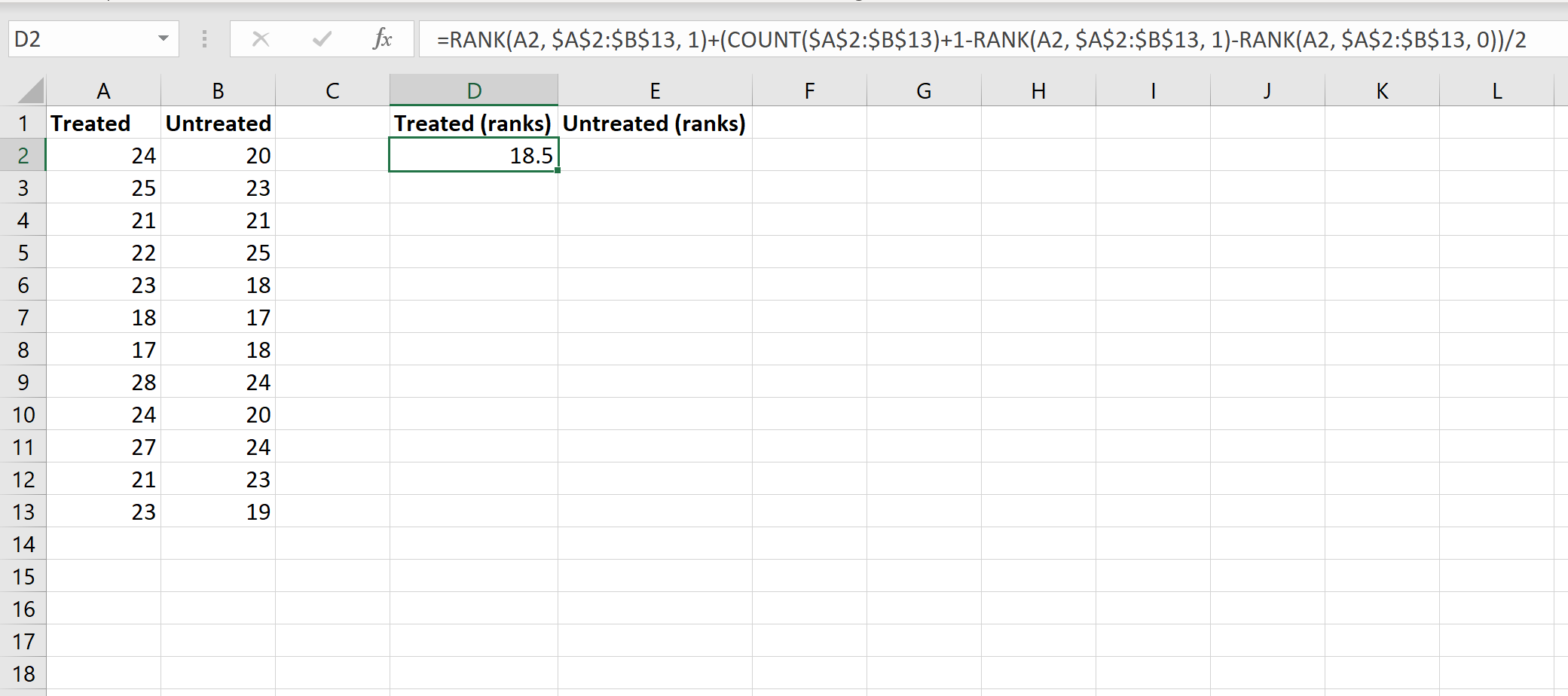
Крок 2: обчисліть рейтинги для обох груп.

Далі ми розрахуємо рейтинги для кожної групи. На наступному зображенні показано формулу для обчислення рангу першого значення в групі Processed:

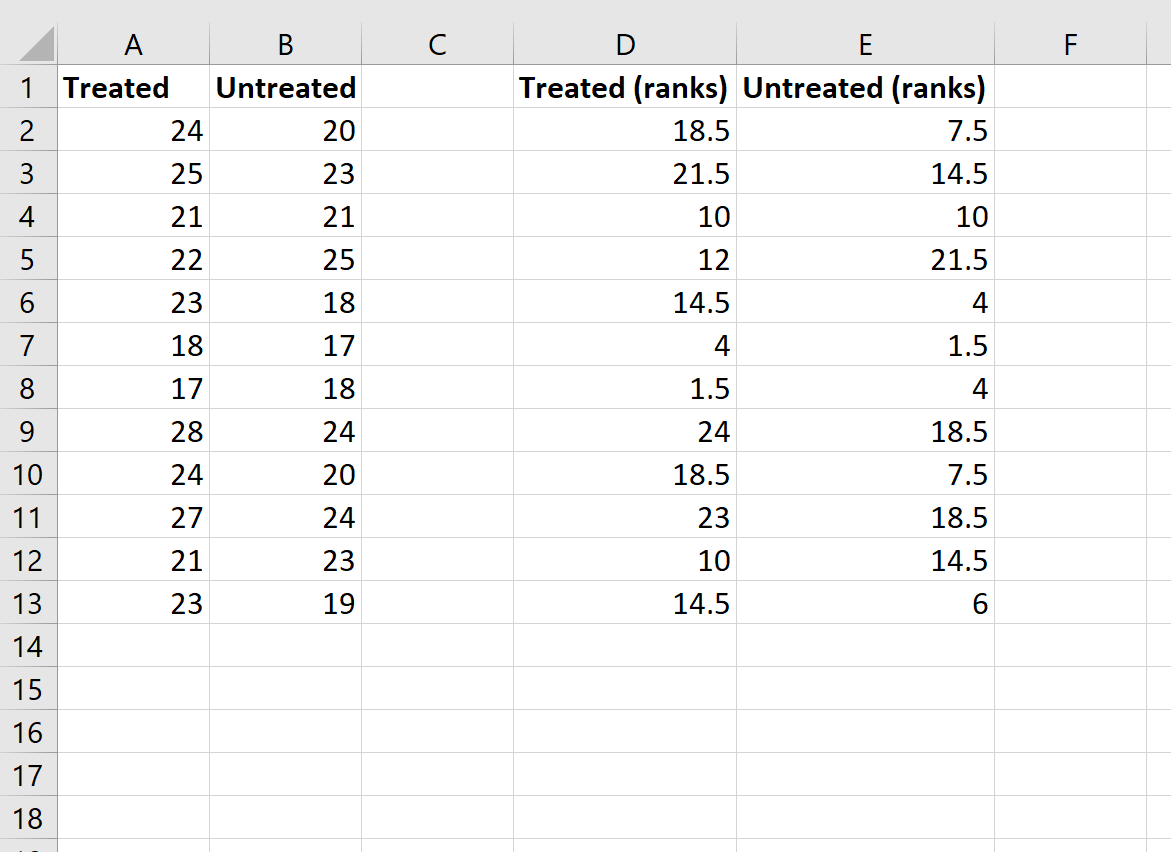
Хоча ця формула досить складна, її потрібно ввести лише один раз. Потім ви можете просто перетягнути формулу в усі інші клітинки, щоб заповнити рядки:

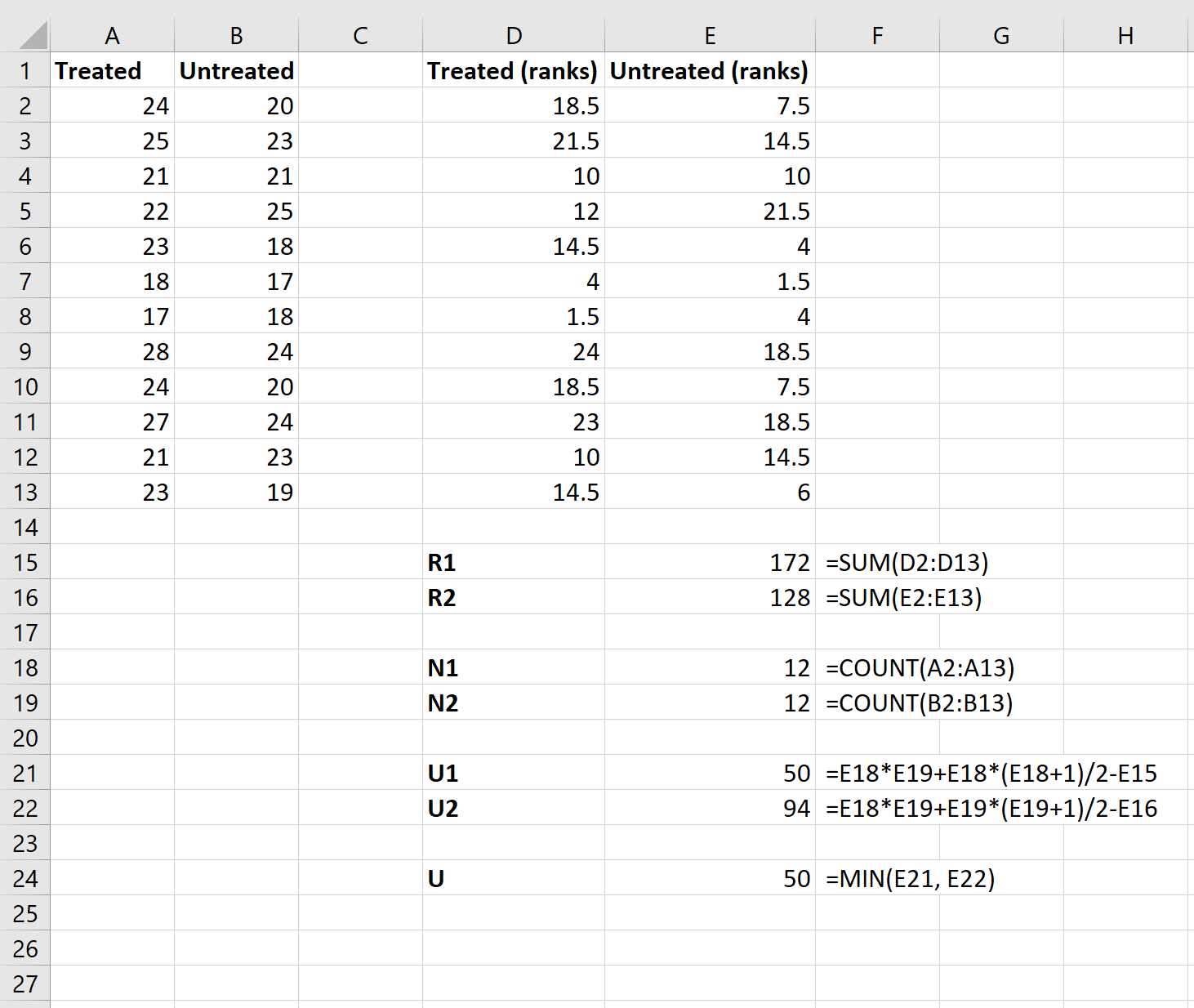
Крок 3: Обчисліть значення, необхідні для тестової статистики.

Далі ми використаємо наступні формули для обчислення суми рангів для кожної групи, розміру вибірки для кожної групи, статистики U-тесту для кожної групи та загальної статистики U-тесту:

Крок 4. Обчисліть статистику z-критерію та відповідне значення p.

Нарешті, ми використаємо наступні формули для обчислення статистики z-критерію та відповідного значення p , щоб визначити, чи слід відхилити нульову гіпотезу чи ні:

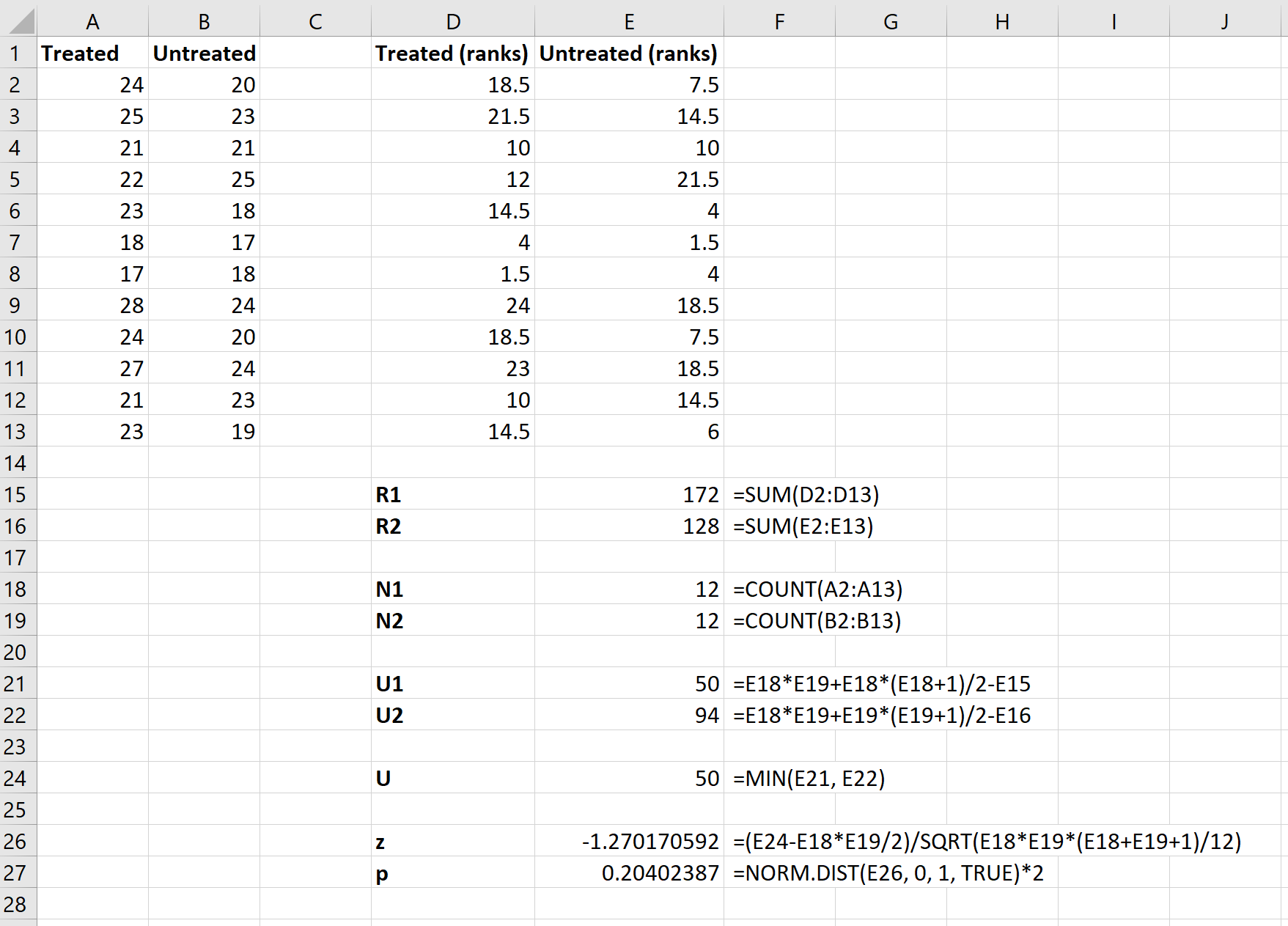
Нульова гіпотеза тесту стверджує, що обидві групи мають однакову середню милю на галон. Оскільки тестове p-значення ( 0,20402387 ) не менше нашого рівня значущості 0,05, ми не можемо відхилити нульову гіпотезу.

Ми не маємо достатньо доказів, щоб стверджувати, що справжня середня кількість миль на галон відрізняється між двома групами.