Як створити та інтерпретувати кореляційну матрицю в excel

Одним із способів кількісного визначення зв’язку між двома змінними є використання коефіцієнта кореляції Пірсона , який є мірою лінійного зв’язку між двома змінними .

Він має значення від -1 до 1, де:

• -1 вказує на абсолютно негативну лінійну кореляцію між двома змінними
• 0 означає відсутність лінійної кореляції між двома змінними
• 1 вказує на абсолютно позитивну лінійну кореляцію між двома змінними

Чим далі коефіцієнт кореляції від нуля, тим сильніший зв’язок між двома змінними.

Але в деяких випадках ми хочемо зрозуміти кореляцію між кількома парами змінних.

У цих випадках ми можемо створити кореляційну матрицю , яка є квадратною таблицею, що показує коефіцієнти кореляції між кількома попарними комбінаціями змінних.

У цьому посібнику пояснюється, як створити та інтерпретувати кореляційну матрицю в Excel.

Як створити кореляційну матрицю в Excel

Скажімо, у нас є такий набір даних, який показує середню кількість очок, підбирань і передач для 10 баскетболістів:

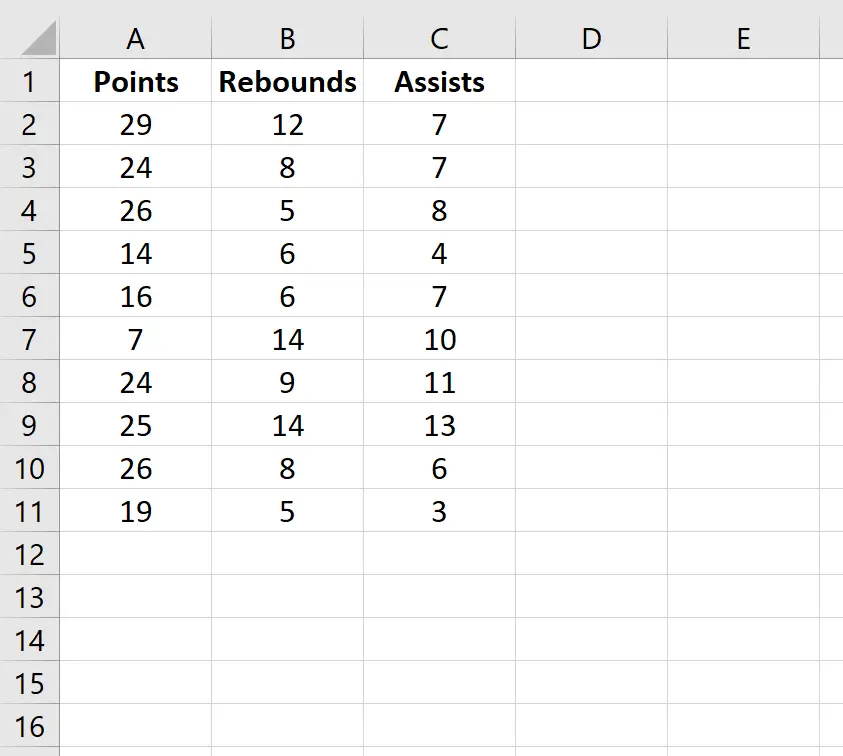
Щоб створити кореляційну матрицю для цього набору даних, перейдіть на вкладку «Дані» у верхній стрічці Excel і натисніть «Аналіз даних» .

Якщо ви не бачите цей параметр, спершу потрібно завантажити безкоштовний Data Analysis Toolpak в Excel .

У новому вікні, що з’явиться, виберіть Кореляція та натисніть OK .

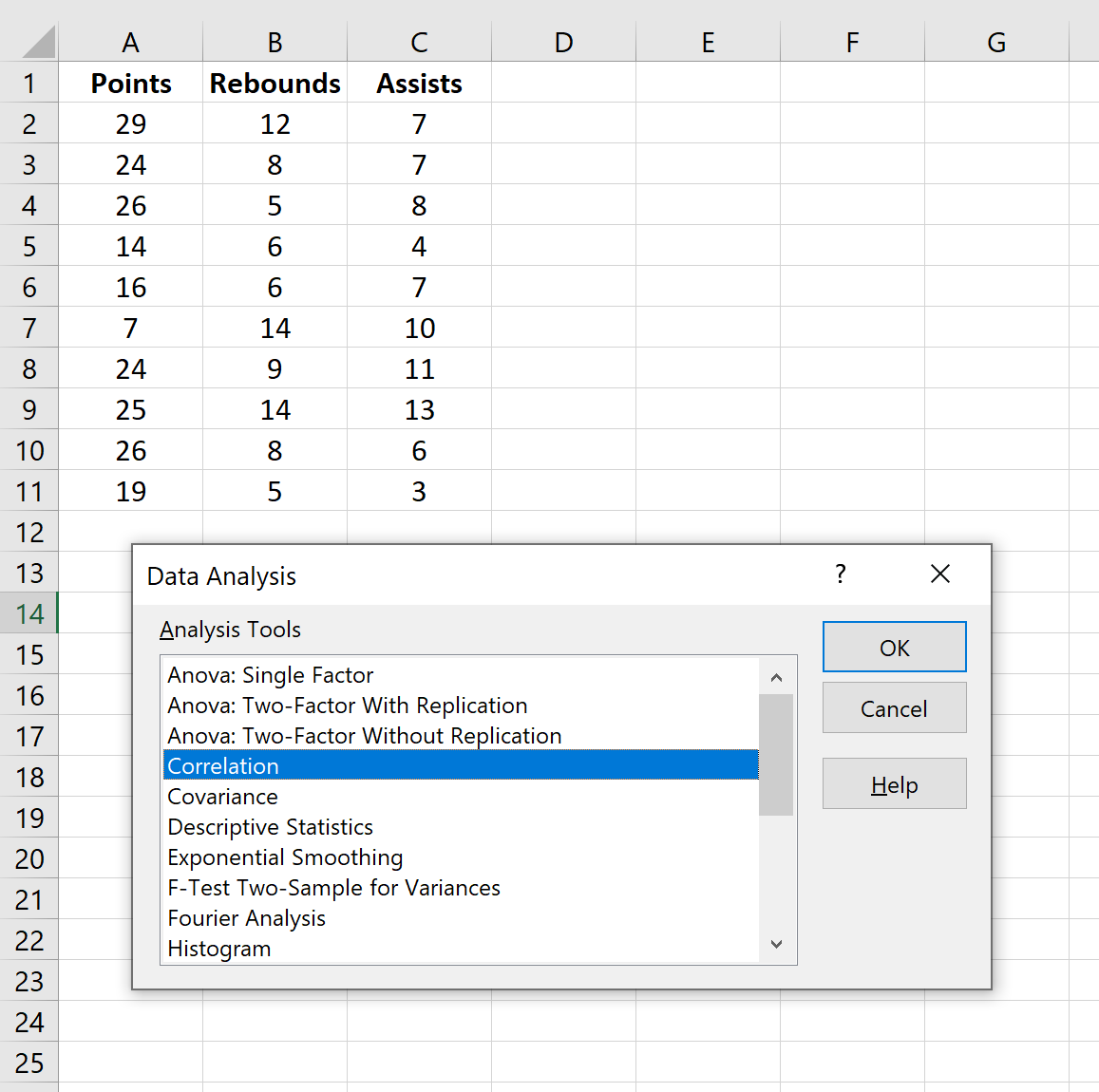
Для параметра «Діапазон введення» виберіть комірки, у яких розташовані дані (включно з першим рядком із мітками). Поставте прапорець біля пункту «Мітки в першому рядку ». Для параметра «Діапазон результатів» виберіть комірку, у якій має відображатися кореляційна матриця. Потім натисніть OK .

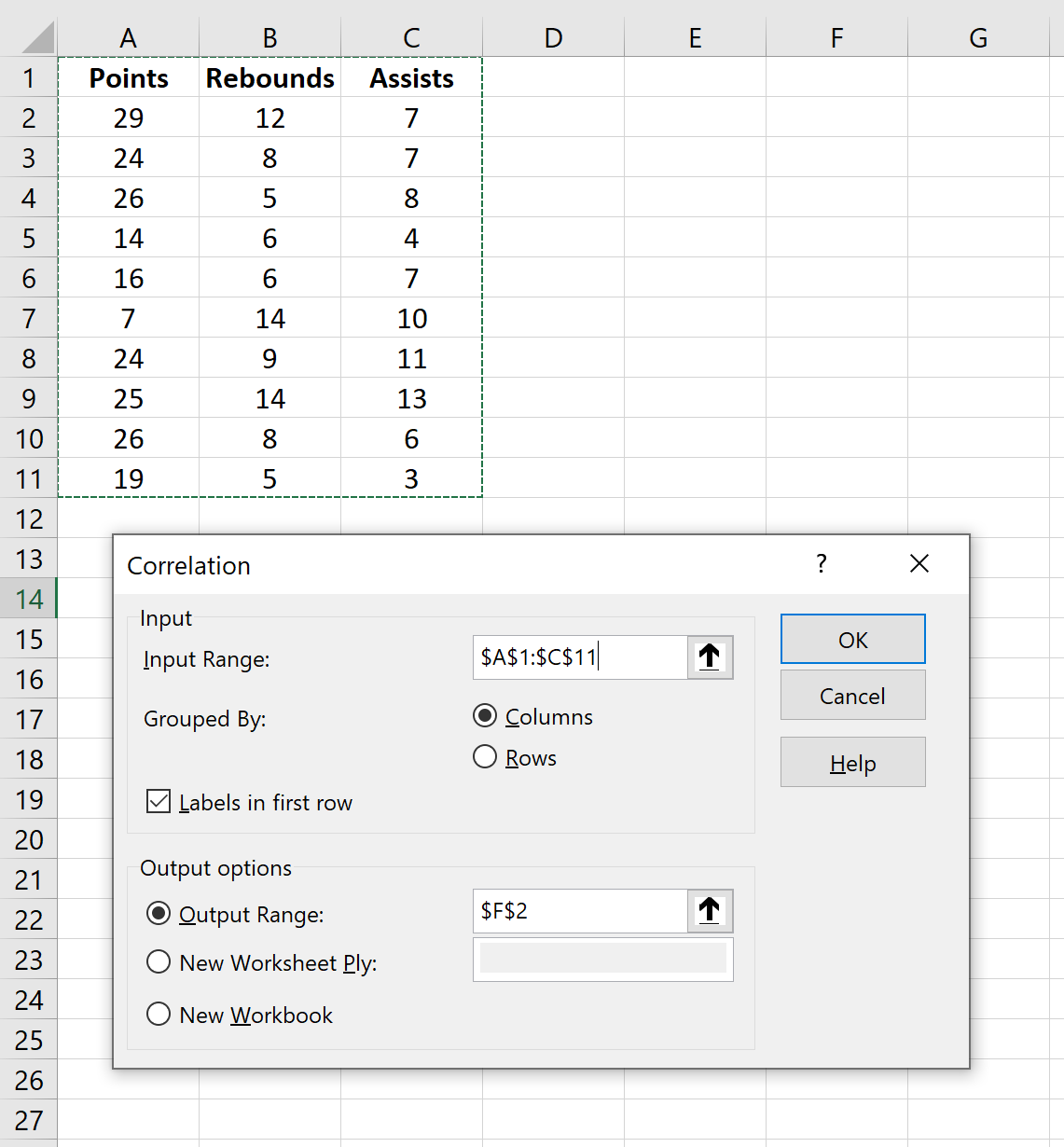
Це автоматично створить таку кореляційну матрицю:

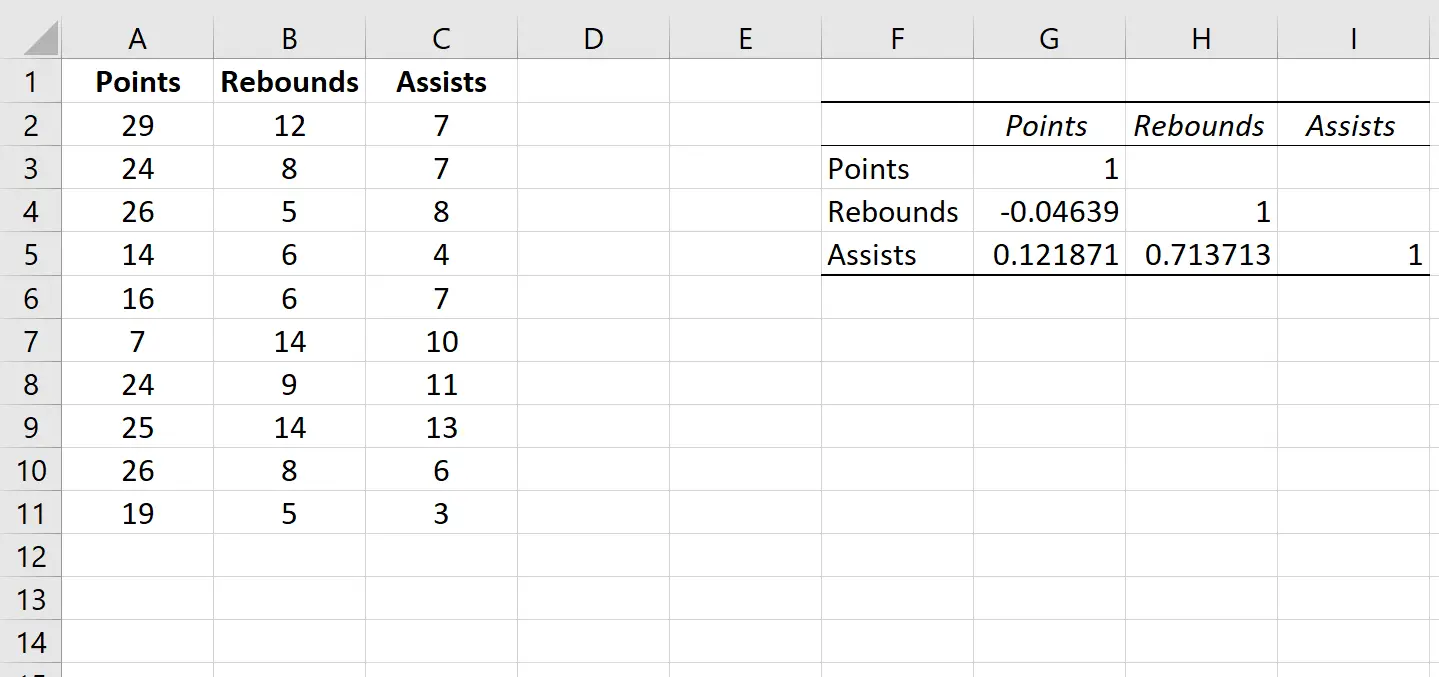
Як інтерпретувати кореляційну матрицю в Excel

Значення в окремих клітинках кореляційної матриці повідомляють нам про коефіцієнт кореляції Пірсона між кожною попарною комбінацією змінних. Наприклад:

Співвідношення між очками та підбираннями: -0,04639. Очки та підбирання трохи негативно корелюють, але це значення настільки близьке до нуля, що немає переконливих доказів значного зв’язку між цими двома змінними.

Співвідношення між очками та передачами: 0,121871. Очки та передачі трохи позитивно корелюють, але це значення також є досить близьким до нуля, тому немає переконливих доказів значного зв’язку між цими двома змінними.

Співвідношення між підбираннями та передачами: 0,713713. Підбирання та передачі сильно позитивно корелюють. Тобто гравці, які мають більше підбирань, також, як правило, мають більше передач.

Зауважте, що всі діагональні значення кореляційної матриці дорівнюють 1, оскільки кореляція між змінною та самою собою завжди дорівнює 1. На практиці це число не корисно інтерпретувати.

Бонус: візуалізуйте коефіцієнти кореляції

Простим способом візуалізації значення коефіцієнтів кореляції в таблиці є застосування до таблиці умовного форматування .

На верхній стрічці Excel перейдіть на вкладку «Головна» , потім групу «Стилі» .

Клацніть Діаграма умовного форматування , потім Колірні шкали , потім Зелено-жовто-червона колірна шкала .

Це автоматично застосовує таку колірну шкалу до кореляційної матриці:

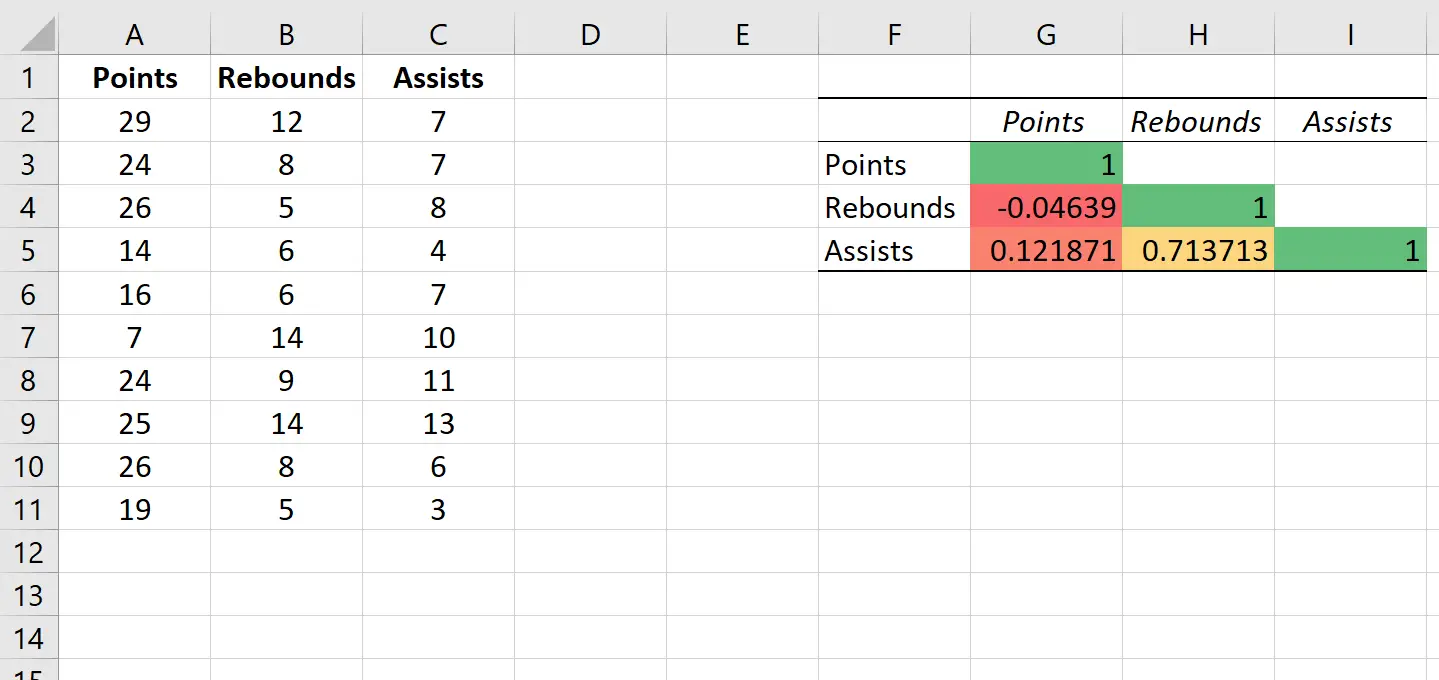
Це допомагає нам легко візуалізувати силу кореляції між змінними.

Це особливо корисна порада, якщо ми працюємо з кореляційною матрицею з багатьма змінними, оскільки вона допомагає нам швидко ідентифікувати змінні, які мають найсильніші кореляції.

За темою: що вважається «сильною» кореляцією?

Додаткові ресурси

У наступних посібниках пояснюється, як виконувати інші типові завдання в R:

Як створити матрицю діаграми розсіювання в Excel
Як виконати кореляційний тест в Excel