Як виконати квадратичну регресію на калькуляторі ti-84

Коли дві змінні мають лінійний зв’язок, ми часто можемо використовувати просту лінійну регресію , щоб кількісно визначити їхній зв’язок.

Однак, коли дві змінні мають квадратичний зв’язок, ми можемо використати квадратичну регресію , щоб кількісно визначити їхній зв’язок.

У цьому посібнику пояснюється, як виконати квадратичну регресію на калькуляторі TI-84.

Приклад: квадратична регресія на калькуляторі TI-84

Припустімо, ми хочемо зрозуміти залежність між кількістю відпрацьованих годин і щастям. У нас є такі дані про кількість відпрацьованих годин на тиждень і рівень щастя (за шкалою від 0 до 100) для 11 різних людей:

Виконайте наступні дії, щоб виконати квадратичну регресію на калькуляторі TI-84.

Крок 1: Візуалізуйте дані.

Перш ніж ми зможемо використовувати квадратичну регресію, ми повинні переконатися, що зв’язок між пояснювальною змінною (годинами) і змінною відповіді (щастям) дійсно є квадратичною.

Спочатку ми введемо значення даних для пояснювальної змінної та змінної відповіді. Натисніть Stat, потім натисніть EDIT . Введіть наступні значення для пояснювальної змінної (відпрацьованих годин) у стовпець L1 і значення для змінної відповіді (щастя) у стовпець L2:

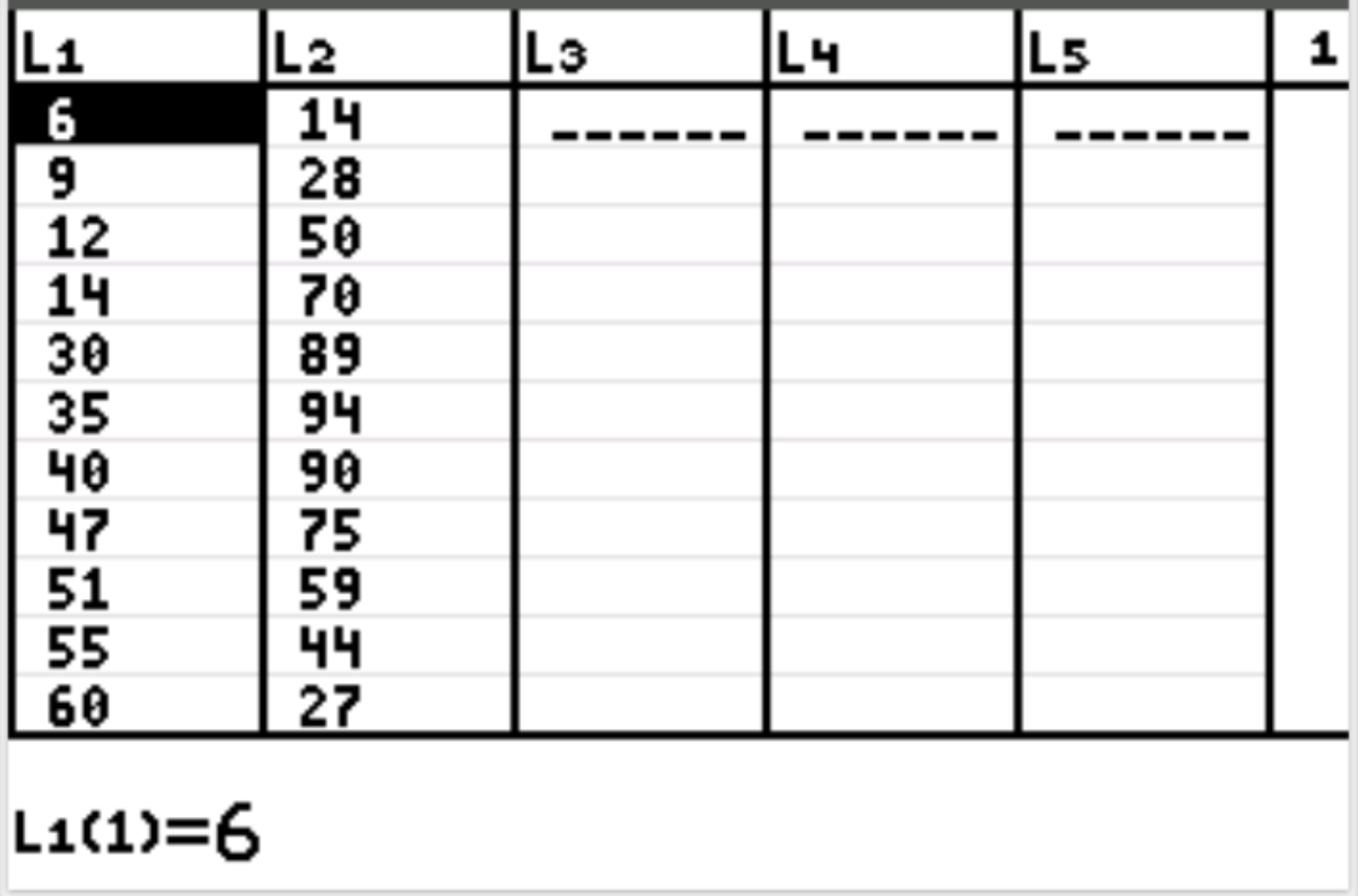
Потім натисніть 2nd, а потім натисніть y= , щоб отримати доступ до меню statplot . Виділіть Plot1 і натисніть Enter . Переконайтеся, що креслення ввімкнено, а L1 і L2 вибрано для Xlist і Ylist відповідно:

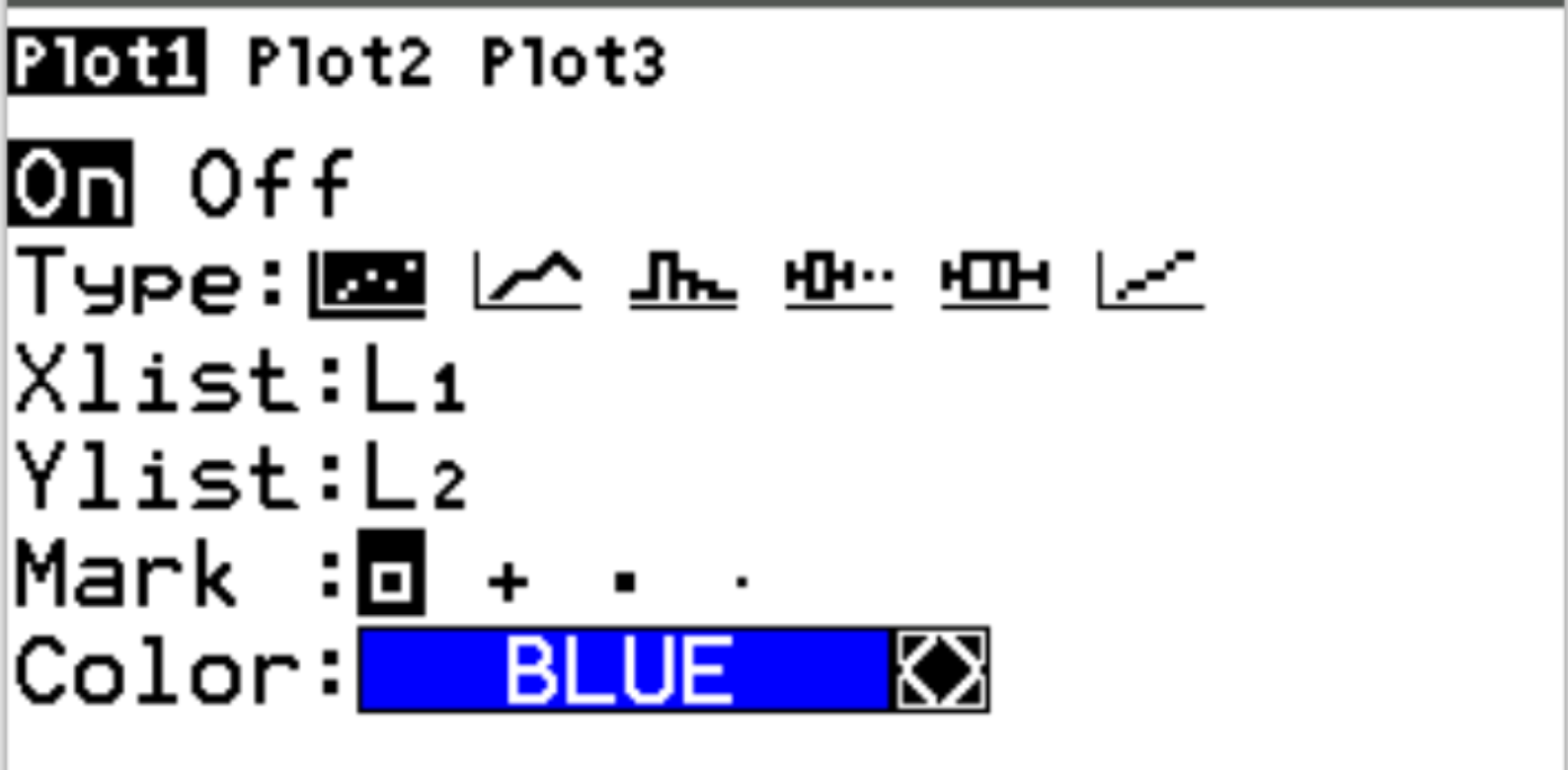
Потім натисніть zoom , а потім 9:ZoomStat . Це автоматично створить таку хмару точок:

Ми бачимо, що щастя має тенденцію до зростання, коли кількість відпрацьованих годин збільшується від нуля до певної точки, але потім починає зменшуватися, коли кількість відпрацьованих годин збільшується.

Ця перевернута буква «U» на діаграмі розсіювання вказує на те, що існує квадратична залежність між відпрацьованими годинами та щастям, що означає, що ми повинні використовувати квадратичну регресію для кількісної оцінки цієї залежності.

Крок 2: Виконайте квадратичну регресію.

Далі ми виконаємо квадратичну регресію. Натисніть Stat, а потім перейдіть до CALC . Потім перейдіть до 5:QuadReg і натисніть Enter .

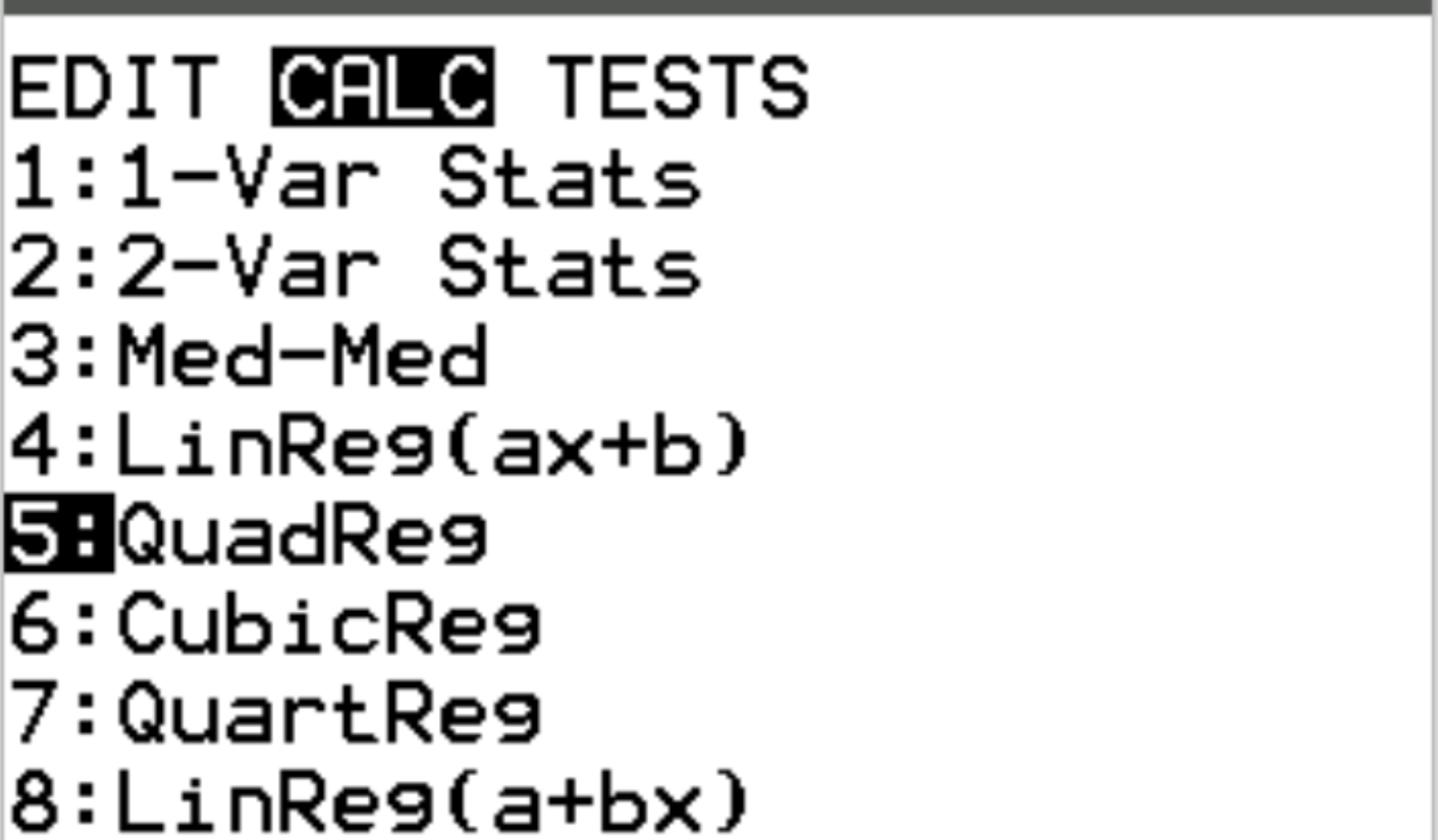
Для Xlist і Ylist переконайтеся, що вибрано L1 і L2, оскільки це стовпці, які ми використовували для введення наших даних. Залиште FreqList порожнім. Прокрутіть униз до пункту «Обчислити» та натисніть «Enter» .

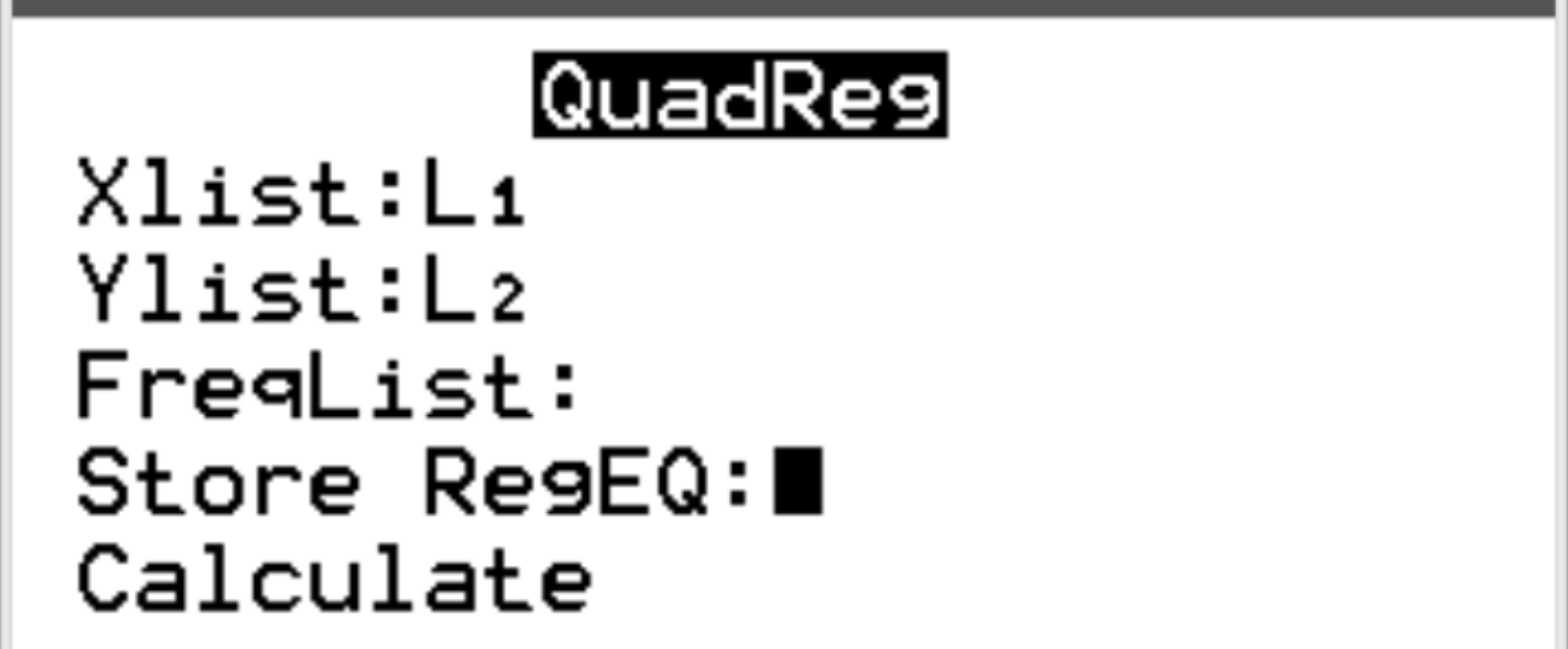
Автоматично з’явиться такий результат:

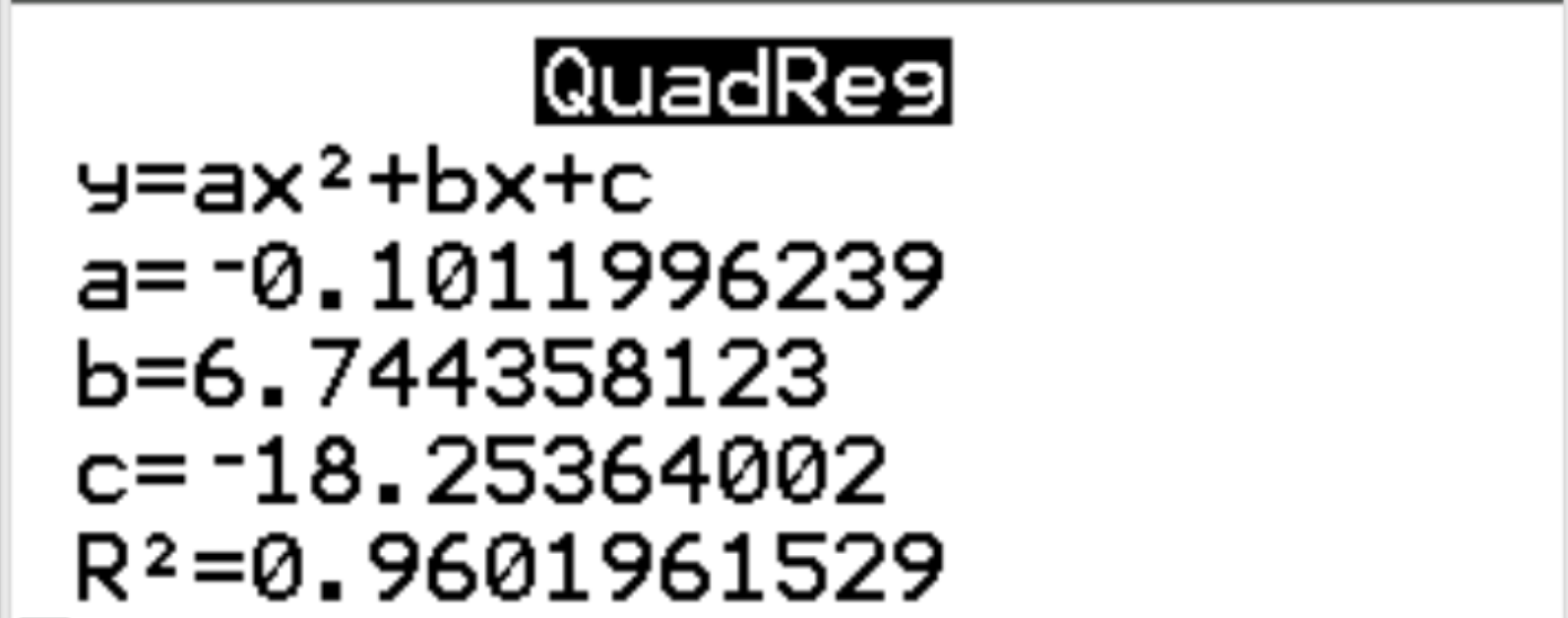
Крок 3: Інтерпретація результату.

З результатів ми бачимо, що оцінене рівняння регресії таке:

щастя = -0,1012 (годин) ² + 6,7444 (годин) – 18,2536

Ми можемо використовувати це рівняння, щоб знайти прогнозоване щастя людини, враховуючи кількість годин, які вони працюють на тиждень.

Наприклад, людина, яка працює 60 годин на тиждень, матиме рівень щастя 22,09 :

щастя = -0,1012(60) ² + 6,7444(60) – 18,2536 = 22,09

І навпаки, людина, яка працює 30 годин на тиждень, повинна мати рівень щастя 92,99 :

щастя = -0,1012(30) ² + 6,7444(30) – 18,2536 = 92,99

Ми також бачимо, що r у квадраті для регресійної моделі становить r ² = 0,9602 . Це частка дисперсії у змінній відповіді, яку можна пояснити пояснювальними змінними. У цьому прикладі 96,02% варіації щастя можна пояснити годинами та часом ² .