Тест хі-квадрат на калькуляторі ti-84

Тест відповідності хі-квадрат використовується для визначення того, чи відповідає категоріальна змінна гіпотетичному розподілу.

У цьому підручнику пояснюється, як виконати тест хі-квадрат на калькуляторі TI-84.

Приклад: Тест хі-квадрат на калькуляторі TI-84

Власник магазину каже, що кожен день тижня до його магазину приходить однакова кількість покупців. Щоб перевірити цю гіпотезу, незалежний дослідник фіксує кількість покупців, які прийшли в магазин за певний тиждень, і знаходить наступне:

• Понеділок: 50 клієнтів
• Вівторок: 60 клієнтів
• Середа: 40 клієнтів
• Четвер: 47 клієнтів
• П’ятниця: 53 клієнтів

Ми використаємо наступні кроки, щоб виконати тест відповідності хі-квадрат, щоб визначити, чи дані відповідають заяві власника магазину.

Крок 1: Введіть дані.

По-перше, ми введемо значення даних для очікуваної кількості клієнтів щодня та спостережуваної кількості клієнтів щодня. Натисніть Stat, потім натисніть EDIT . Введіть наступні значення для спостережуваної кількості клієнтів у стовпці L1 та значення для очікуваної кількості клієнтів у стовпці L2:

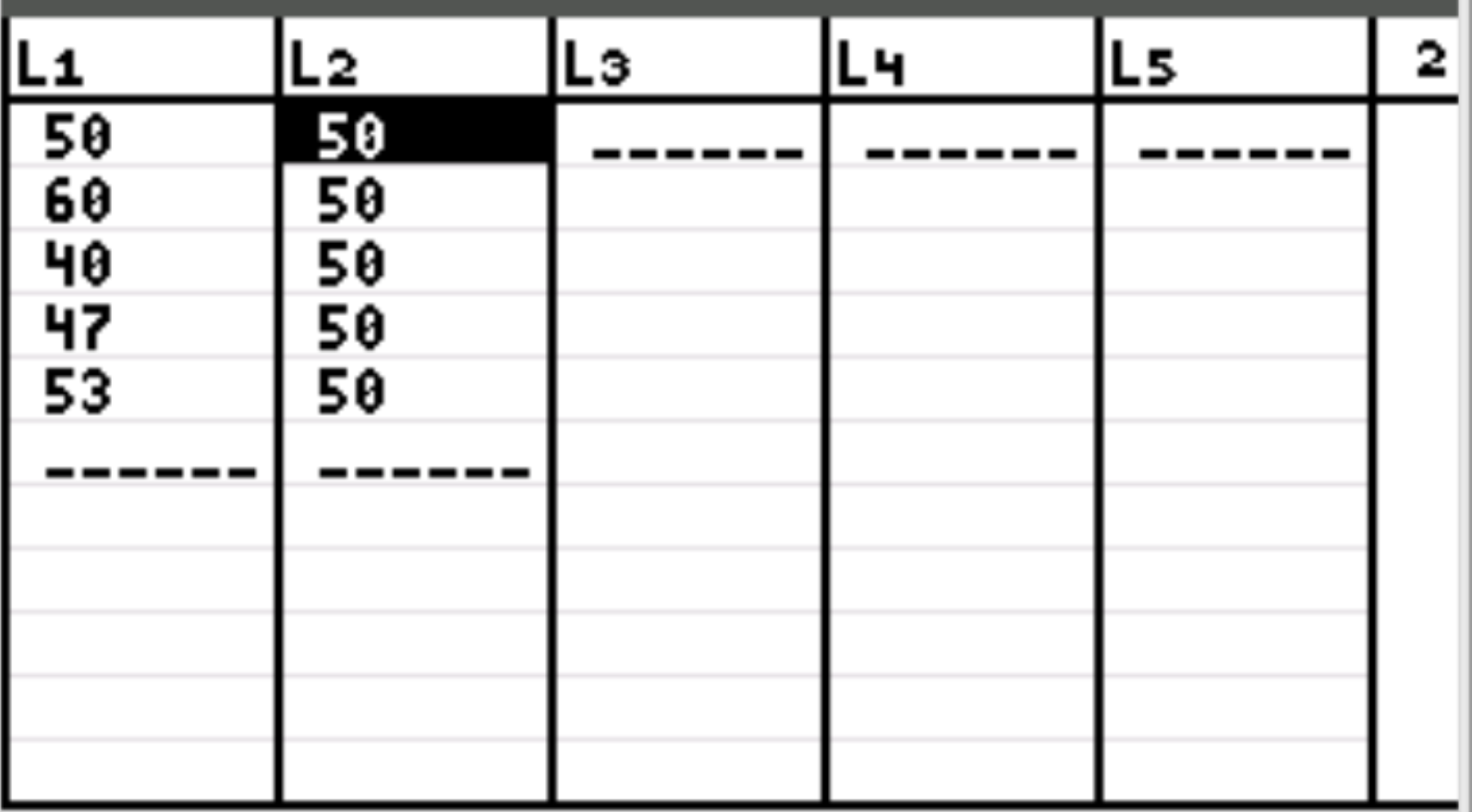
Примітка. Загалом було 250 клієнтів. Отже, якщо власник магазину очікує, що щодня до магазину заходитиме однакова кількість покупців, це буде 50 покупців на день.

Крок 2. Виконайте тест на відповідність хі-квадрат.

Далі ми виконаємо тест на відповідність хі-квадрат. Натисніть Stat, а потім перейдіть до TESTS . Потім прокрутіть вниз до X ² GOF-Test і натисніть Enter .

Для Observed виберіть список L1. Для Expected виберіть список L2. Для df (ступенів свободи) введіть #categories – 1. У нашому випадку ми маємо 5-1 = 4. Потім виділіть Calculate і натисніть Enter .

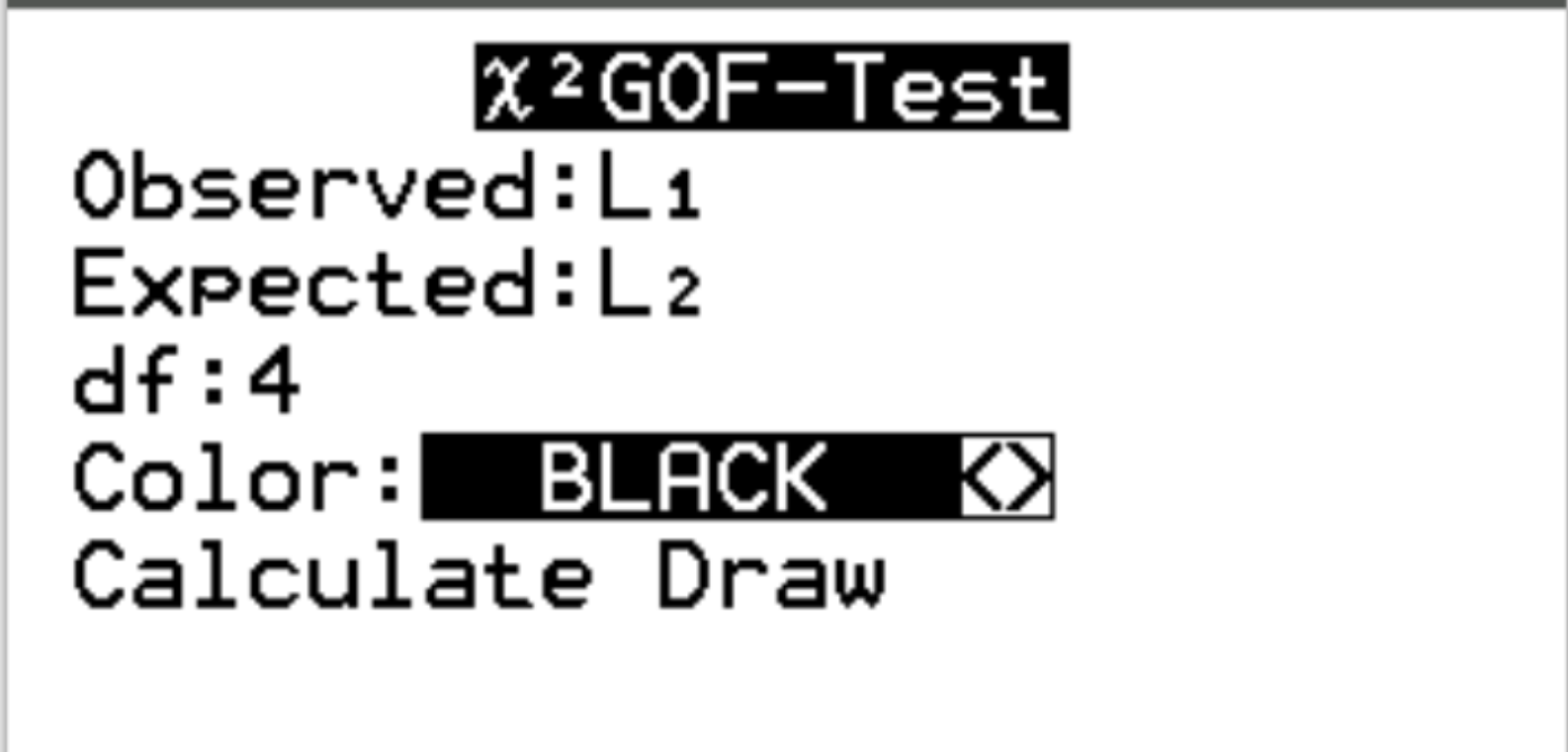
Автоматично з’явиться такий результат:

Крок 3: Інтерпретація результатів.

Статистика тесту ^X2 для тесту становить 4,36 , а відповідне значення p — 0,3595 . Оскільки це p-значення не менше 0,05, ми не можемо відхилити нульову гіпотезу. Це означає, що ми не маємо достатньо доказів, щоб стверджувати, що справжній розподіл клієнтів відрізняється від того, про який повідомляє власник магазину.