Як читати таблицю біноміального розподілу

Біноміальна таблиця розподілу   це таблиця, яка показує ймовірності, пов’язані з біноміальним розподілом . Щоб використовувати таблицю біноміального розподілу, вам потрібні лише три значення:

• n: кількість спроб
• r: кількість «успіхів» під час n спроб
• p: ймовірність успіху даного випробування

Використовуючи ці три числа, ви можете використовувати таблицю біноміального розподілу, щоб знайти ймовірність отримати рівно r успіхів протягом n випробувань, коли ймовірність успіху в кожному випробуванні дорівнює p .

Наступні приклади ілюструють, як читати таблицю біноміального розподілу.

Приклад 1

Запитання: Джессіка виконує 60% своїх штрафних кидків. Якщо вона виконує 6 штрафних кидків, яка ймовірність того, що вона зробить рівно 4?

Щоб відповісти на це запитання, ми можемо знайти значення в таблиці біноміального розподілу, яке відповідає n = 6, r = 4 і p = 0,60:

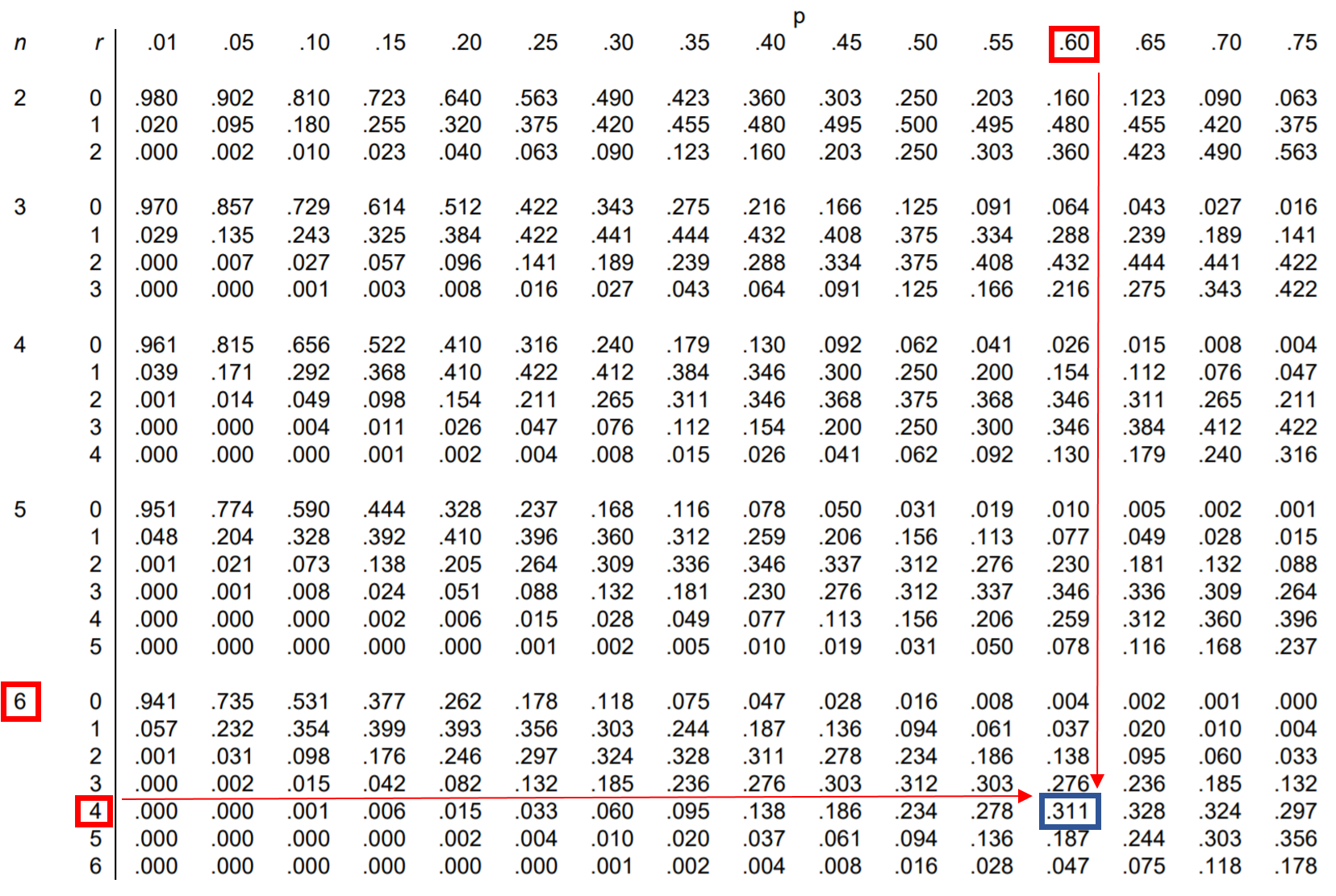
Імовірність того, що Джессіка виконує рівно 4 з 6 штрафних кидків, дорівнює 0,311 .

Приклад 2

Запитання: Джессіка виконує 60% своїх штрафних кидків. Якщо вона виконує 6 штрафних кидків, яка ймовірність того, що вона зробить менше 4?

Щоб знайти цю ймовірність, ви фактично повинні додати такі ймовірності:

P (утворює менше 4) = P (утворює 0) + P (утворює 1) + P (утворює 2) + P (утворює 3)

Отже, ми можемо знайти кожну з цих чотирьох ймовірностей у таблиці біноміального розподілу та додати їх разом:

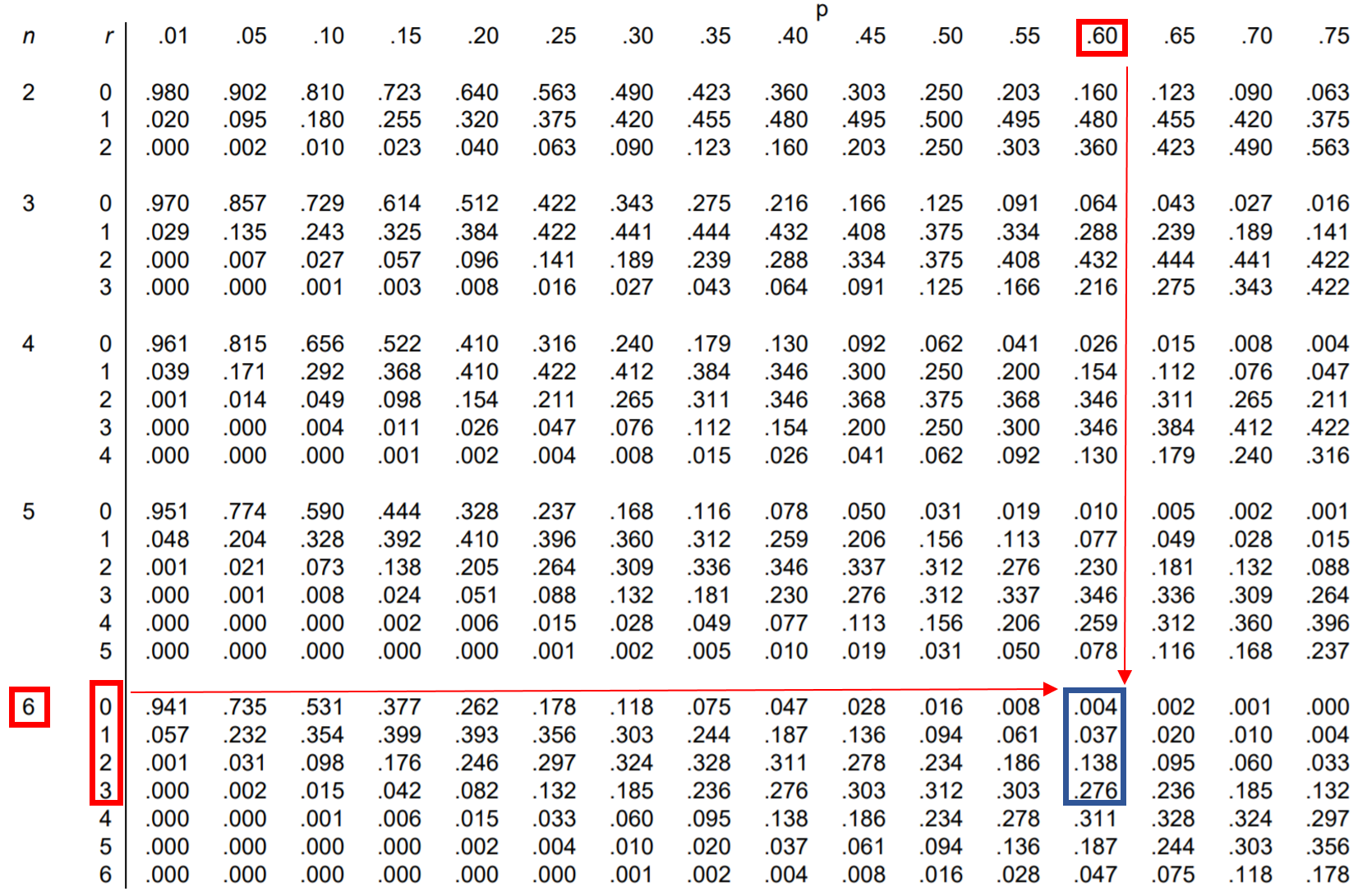
З таблиці P (менше 4) = 0,004 + 0,037 + 0,138 + 0,276 = 0,455 .

Імовірність того, що Джессіка зробить менше 4 штрафних кидків, дорівнює 0,455 .

Приклад 3

Запитання: Джессіка виконує 60% своїх штрафних кидків. Якщо вона виконує 6 штрафних кидків, яка ймовірність того, що вона зробить 4 або більше?

Щоб знайти цю ймовірність, ми повинні додати такі ймовірності:

P (утворює 4 або більше) = P (утворює 4) + P (утворює 5) + P (утворює 6)

Отже, ми можемо знайти кожну з цих трьох ймовірностей у таблиці біноміального розподілу та скласти їх разом:

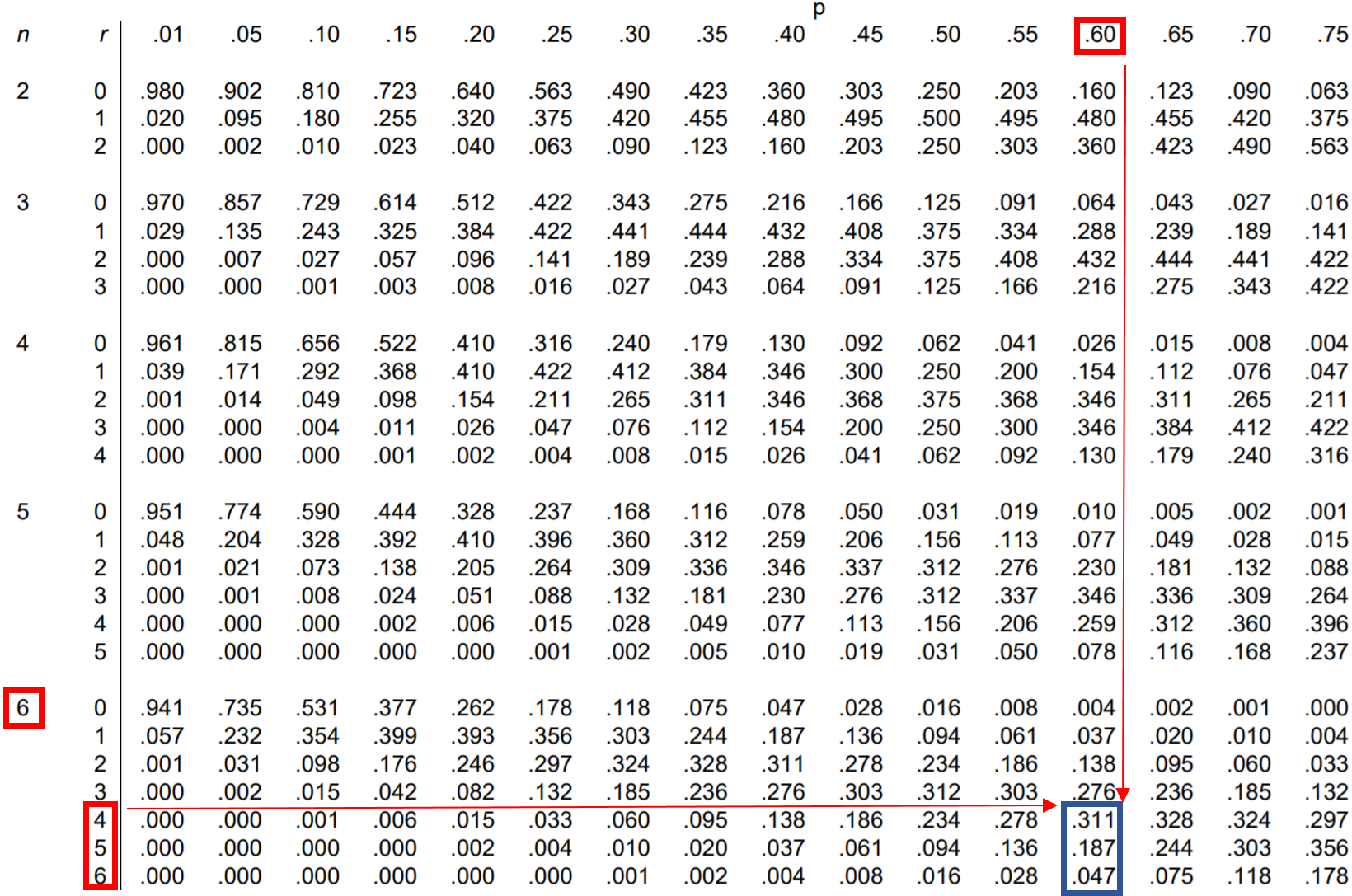
З таблиці P (становить 4 або більше) = 0,311 + 0,187 + 0,047 = 0,545 .

Імовірність того, що Джессіка виконає 4 або більше штрафних кидків, дорівнює 0,545 .