Як виконати тест левена в spss

Критерій Левена використовується для визначення того, чи мають дві чи більше групи рівні дисперсії.

Він широко використовується, оскільки багато статистичних тестів спираються на припущення, що групи мають однакові дисперсії .

Цей підручник пояснює, як виконати тест Левена в SPSS.

Приклад: тест Лівена в SPSS

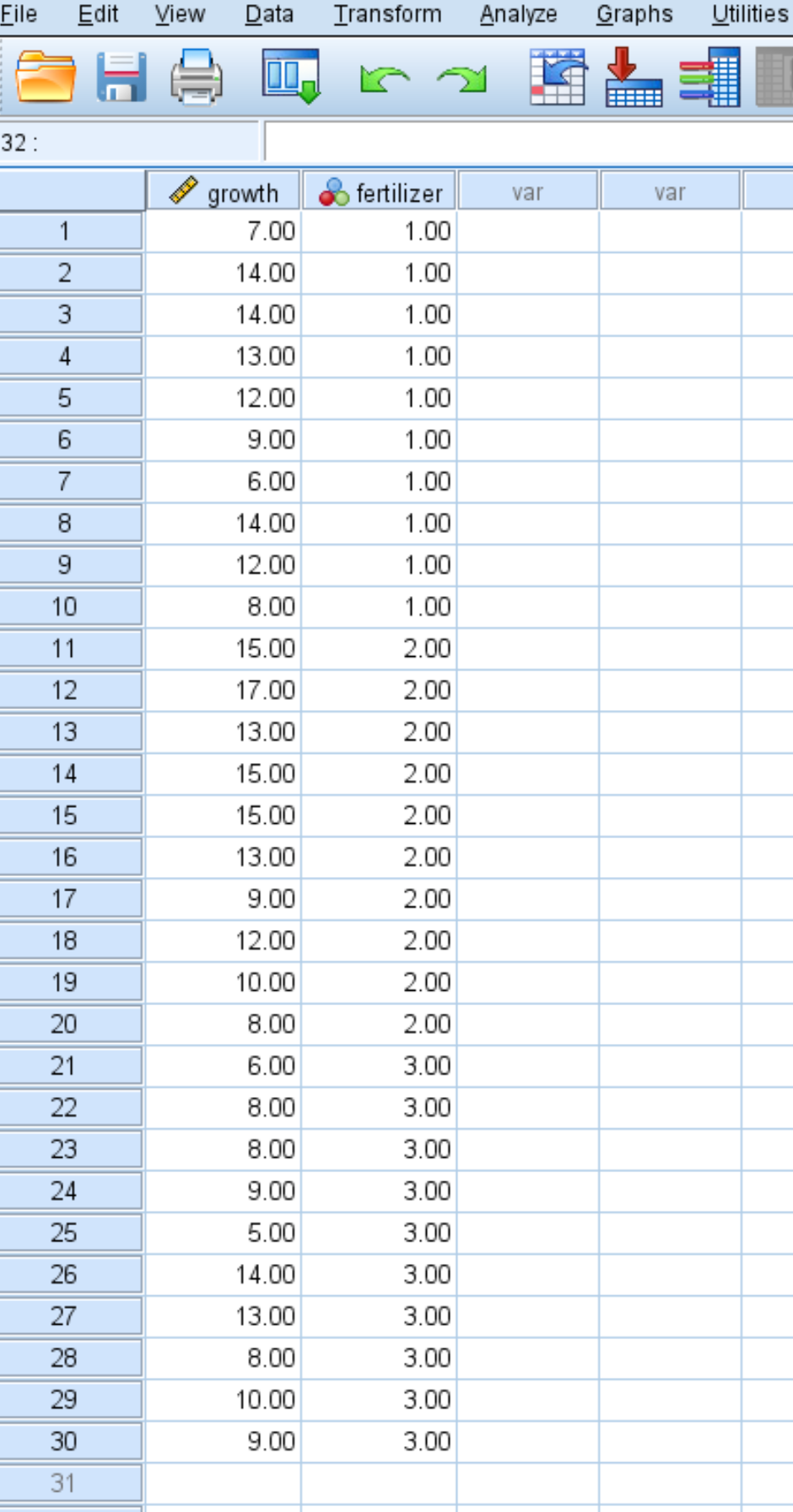
Дослідники хочуть знати, чи призводять три різні добрива до різного рівня росту рослин.

Вони випадковим чином вибирають 30 різних рослин і ділять їх на три групи по 10 рослин, вносячи в кожну групу різні добрива. Через місяць вимірюють висоту кожної рослини.

На наступному знімку екрана показано кількість росту (у дюймах) для кожної окремої рослини разом із добривом (1, 2 або 3), яке було застосовано до рослини:

Виконайте наступні кроки, щоб виконати тест Лівена в SPSS, щоб визначити, чи мають три групи однакові дисперсії.

Крок 1. Виберіть опцію «Дослідити».

Натисніть вкладку «Аналіз» , потім «Описова статистика» , а потім «Дослідження» :

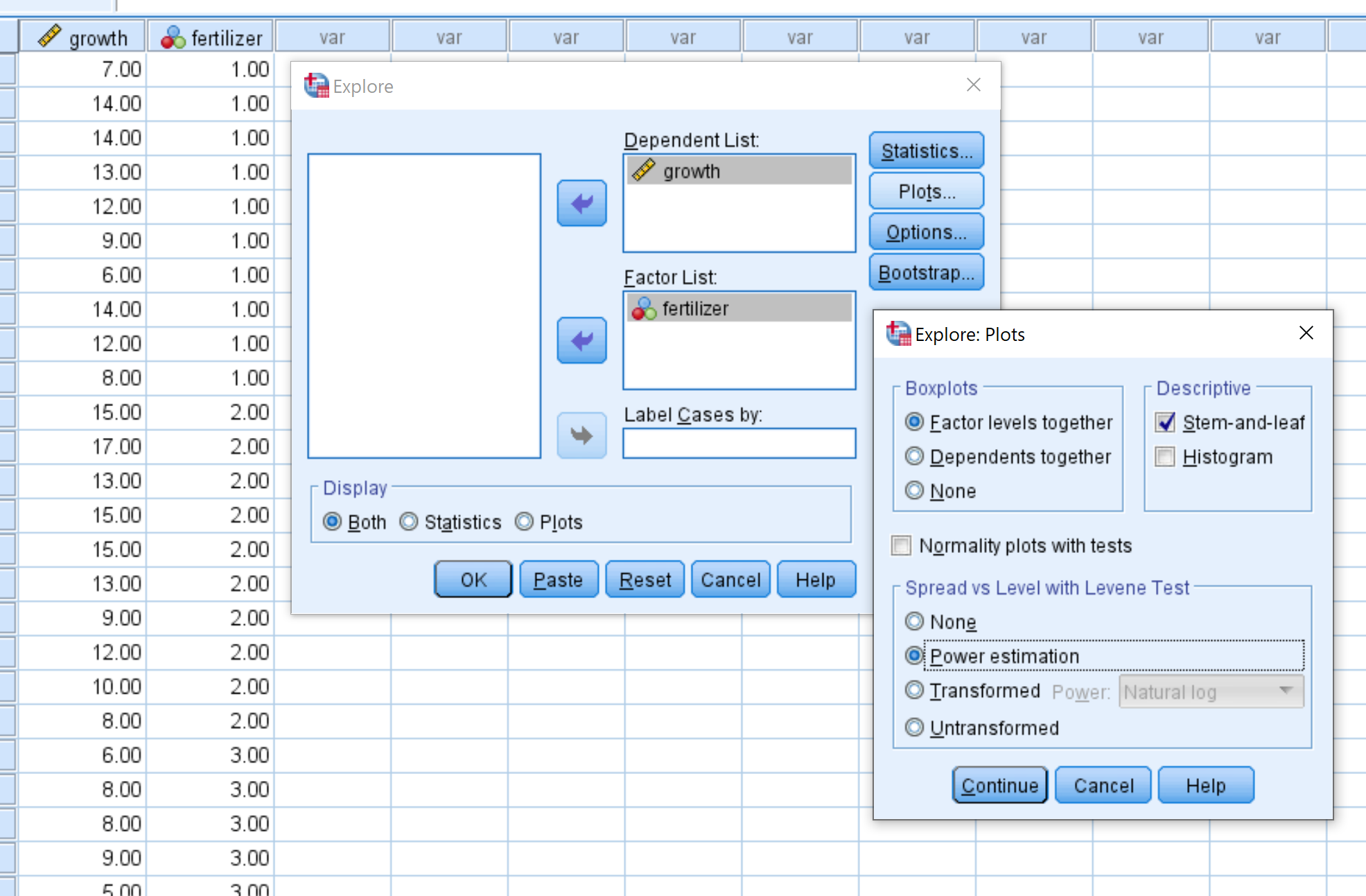
Крок 2: Заповніть необхідні значення для виконання тесту.

Перетягніть зростання в поле в списку залежних і перетягніть удобрення   у полі під Списком факторів.

Потім натисніть «Графіки» та переконайтеся, що вибрано «Оцінка потужності» . Потім натисніть продовжити . Потім натисніть OK .

Крок 3: Інтерпретація результатів.

Після натискання кнопки OK відобразяться результати тесту Levene:

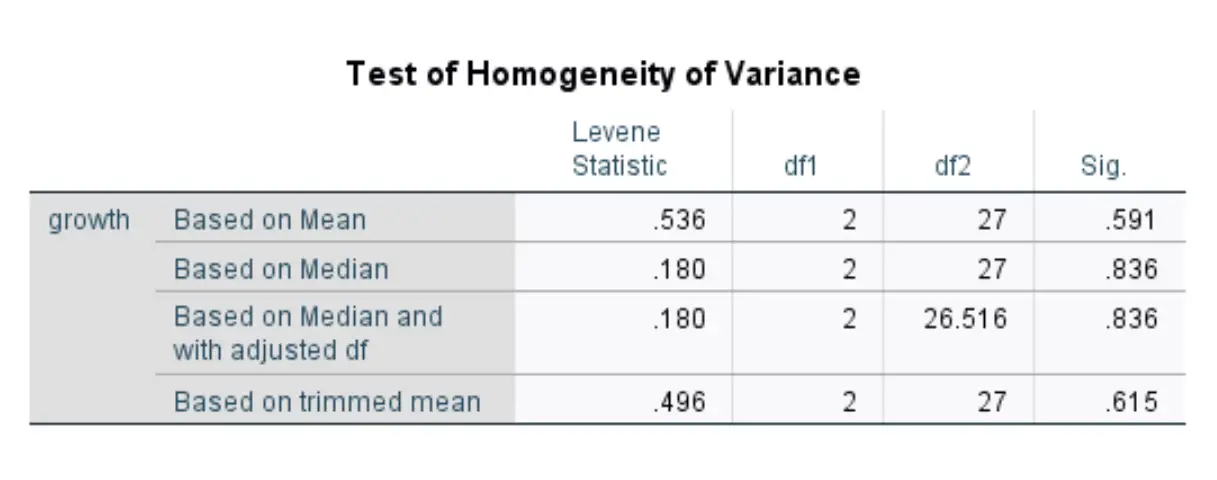
Ця таблиця відображає статистику тесту для чотирьох різних версій тесту Левена. Числа, які нас цікавлять, знаходяться в першому рядку, який відображає результати тесту Левена на основі середнього.

Статистика тесту становить 0,536 , а відповідне значення p — 0,591* .

Оскільки це p-значення не менше 0,05, ми не можемо відхилити нульову гіпотезу.

Це означає, що ми не маємо достатніх доказів, щоб стверджувати, що різниця у зростанні рослин між трьома добривами значно відрізняється.

Іншими словами, три групи мають рівні дисперсії. Якби ми провели статистичний тест (наприклад , односторонній дисперсійний аналіз ), який припускає, що кожна група має однакову дисперсію, тоді це припущення буде виконано.

* Це p-значення відповідає F-статистиці 0,536 з чисельником df = 2 і знаменником df = 27. Це p-значення також можна обчислити за допомогою калькулятора F-розподілу.