Як використовувати біноміальний розподіл у python

Біноміальний розподіл є одним із найбільш часто використовуваних розподілів у статистиці. Він описує ймовірність отримання k успіхів у n біноміальних експериментах.

Якщо випадкова величина X відповідає біноміальному розподілу, то ймовірність успіху X = k можна знайти за такою формулою:

P(X=k) = _n C _k * p ^k * (1-p) ^nk

золото:

• n: кількість випробувань
• k: кількість успіхів
• p: ймовірність успіху в даному випробуванні
• _n C _k : кількість способів отримати k успіхів у n випробуваннях

Цей посібник пояснює, як використовувати біноміальний розподіл у Python.

Як створити біноміальний розподіл

Ви можете створити масив значень, який відповідає біноміальному розподілу, використовуючи функцію random.binomial бібліотеки numpy:

 from numpy import random

#generate an array of 10 values that follows a binomial distribution
random.binomial(n=10, p=.25, size=10)

array([5, 2, 1, 3, 3, 3, 2, 2, 1, 4])

Кожне число в результуючій таблиці представляє кількість «успішних результатів», отриманих протягом 10 випробувань, де ймовірність успіху в даному випробуванні становила 0,25 .

Як обчислити ймовірності за допомогою біноміального розподілу

Ви також можете відповісти на запитання про біноміальну ймовірність за допомогою функції binom бібліотеки scipy.

Запитання 1: Натан виконує 60% своїх спроб штрафних кидків. Якщо він виконує 12 штрафних кидків, яка ймовірність того, що він зробить рівно 10?

 from scipy.stats import binom

#calculate binomial probability
binom.pmf(k= 10 , n= 12 , p= 0.6 )

0.0639

Імовірність того, що Натан виконає рівно 10 штрафних кидків, дорівнює 0,0639 .

Запитання 2: Марті підкидає монету 5 разів. Яка ймовірність того, що монета випаде головою 2 рази чи менше?

 from scipy.stats import binom

#calculate binomial probability
binom.cdf(k= 2 , n= 5 , p= 0.5 )

0.5

Імовірність того, що монета випаде головами 2 рази або менше, становить 0,5 .

Запитання 3: Ми знаємо, що 70% людей підтримують певний закон. Якщо навмання вибрати 10 осіб, яка ймовірність того, що від 4 до 6 із них підтримають закон?

 from scipy.stats import binom

#calculate binomial probability
binom.cdf(k= 6 , n= 10 , p= 0.7 ) - binom.cdf(k= 3 , n= 10 , p= 0.7 )

0.3398

Імовірність того, що від 4 до 6 випадково вибраних осіб підтримують закон, становить 0,3398 .

Як візуалізувати біноміальний розподіл

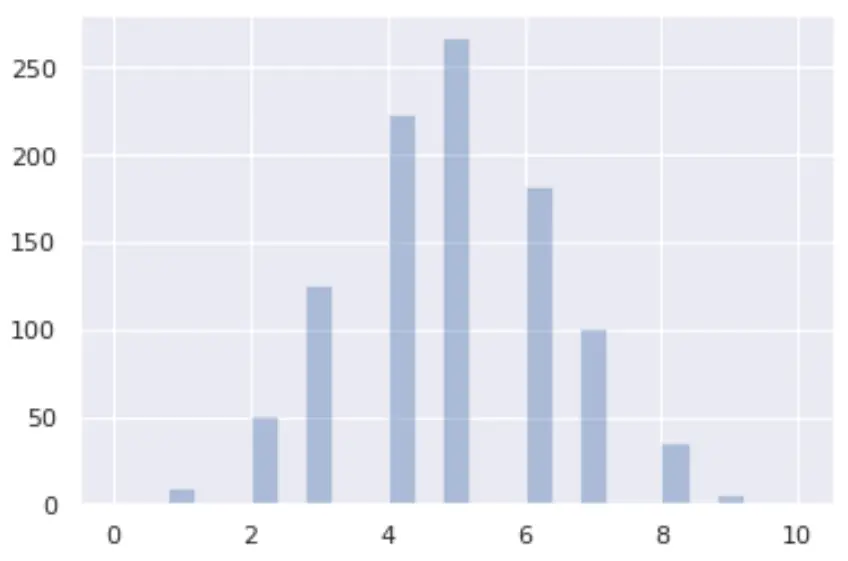
Ви можете візуалізувати біноміальний розподіл у Python за допомогою бібліотек seaborn і matplotlib :

 from numpy import random
import matplotlib.pyplot as plt
import seaborn as sns

x = random.binomial(n= 10 , p= 0.5 , size= 1000 )

sns.distplot(x, hist= True , kde= False )

plt.show()

чай