Стандартне відхилення та стандартна помилка: у чому різниця?

Два терміни, які студенти часто плутають у статистиці, це стандартне відхилення та стандартна помилка .

Стандартне відхилення вимірює розподіл значень у наборі даних.

Стандартна помилка – це стандартне відхилення середнього значення повторних вибірок із сукупності.

Давайте розглянемо приклад, щоб наочно проілюструвати цю ідею.

Приклад: стандартне відхилення проти стандартної помилки

Припустимо, ми вимірюємо вагу 10 різних черепах.

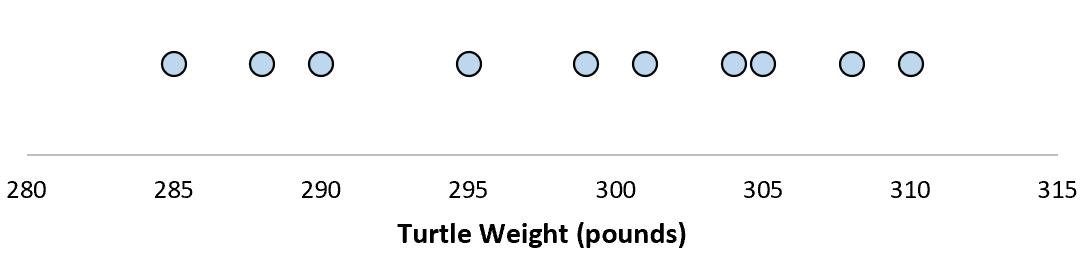
Для цієї вибірки з 10 черепах ми можемо обчислити середнє значення вибірки та стандартне відхилення вибірки:

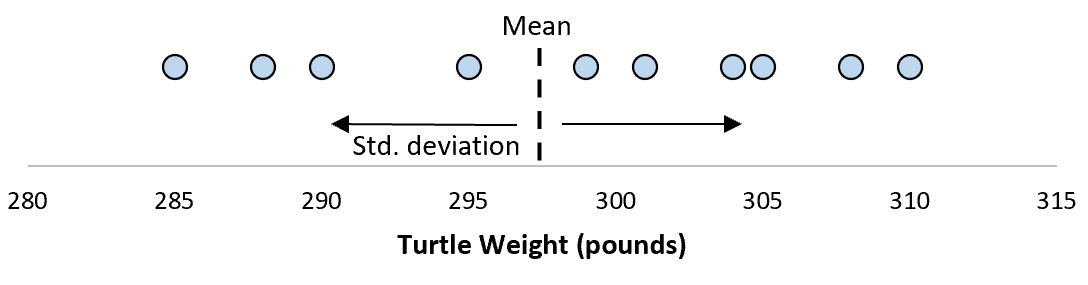
Припустимо, стандартне відхилення дорівнює 8,68. Це дає нам уявлення про розподіл ваги цих черепах.

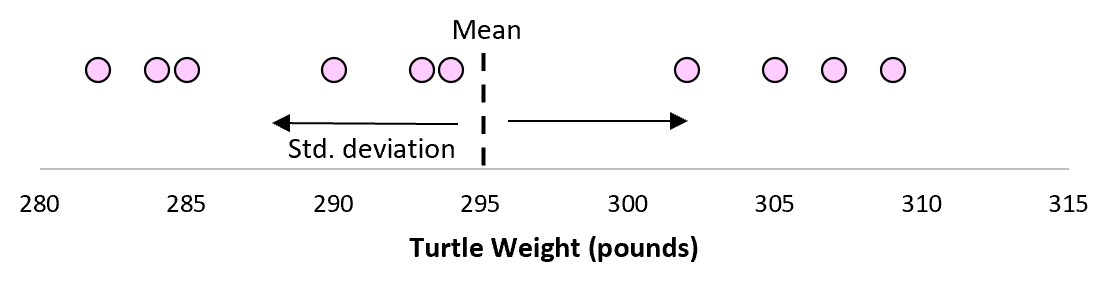
Але припустімо, що ми збираємо ще одну просту випадкову вибірку з 10 черепах і також проводимо їх вимірювання.

Цілком імовірно, що ця вибірка з 10 черепах матиме дещо інше середнє значення та стандартне відхилення, навіть якщо вони походять з однієї популяції:

Тепер, якщо ми уявимо, що ми беремо повторні зразки з тієї самої сукупності та записуємо середнє значення вибірки та стандартне відхилення вибірки для кожної вибірки:

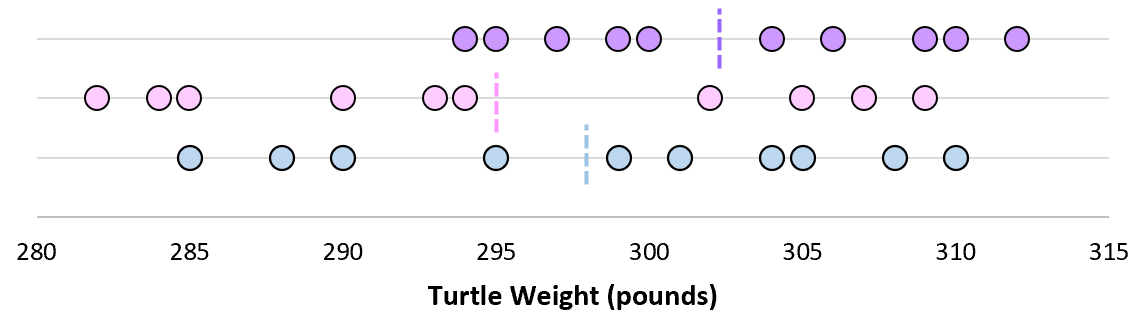
Тепер уявіть, що ми малюємо кожне з вибіркових середніх на одній лінії:

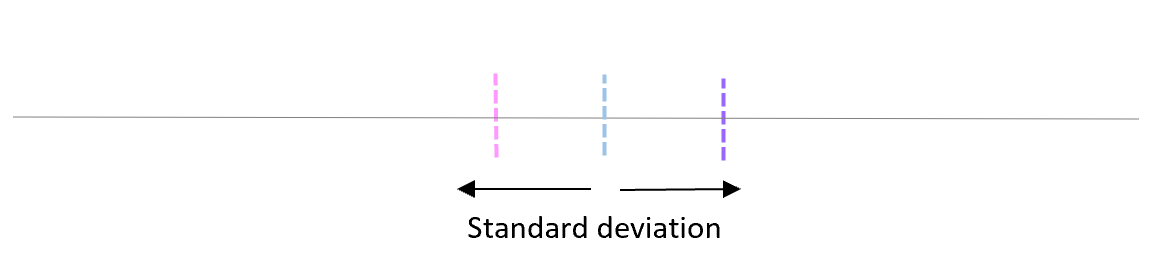
Стандартне відхилення цих середніх значень називається стандартною помилкою.

Формула фактичного обчислення стандартної похибки така:

Стандартна похибка = s/ √ n

золото:

• s: вибіркове стандартне відхилення
• n: розмір вибірки

Який сенс використання стандартної помилки?

Коли ми обчислюємо середнє значення даної вибірки, ми насправді хочемо дізнатися середнє значення цієї конкретної вибірки, а скоріше середнє значення більшої сукупності, з якої походить вибірка.

Однак ми використовуємо вибірки, оскільки для них набагато легше зібрати дані, ніж для всієї сукупності.

І, звісно, вибіркове середнє варіюється від зразка до зразка, тому ми використовуємо стандартну помилку середнього як спосіб вимірювання точності нашої оцінки середнього.

У формулі для обчислення стандартної похибки ви помітите, що зі збільшенням розміру вибірки (n) стандартна похибка зменшується:

Стандартна похибка = s/ √ n

Це мало б мати сенс, оскільки більші вибірки зменшують мінливість і збільшують шанси того, що наше середнє значення вибірки буде ближче до справжнього середнього значення сукупності.

Коли використовувати стандартне відхилення проти стандартної помилки

Якщо ми просто хочемо виміряти розподіл значень у наборі даних, ми можемо використовувати стандартне відхилення .

Однак, якщо ми хочемо кількісно визначити невизначеність навколо оцінки середнього, ми можемо використати стандартну помилку середнього .

Залежно від конкретного сценарію та того, що ви намагаєтеся досягти, ви можете вибрати стандартне відхилення або стандартну помилку.