Як виконати anova з нерівними розмірами вибірки

Питання, яке студенти часто задають, коли йдеться про статистику:

Чи можливо виконати односторонній дисперсійний аналіз, коли розміри вибірки кожної групи не однакові?

Коротка відповідь:

Так, ви можете виконати односторонній дисперсійний аналіз, якщо розміри вибірки не однакові. Рівні розміри вибірки не є одним із припущень, зроблених у ANOVA.

Однак є дві потенційні проблеми, які слід враховувати під час виконання одностороннього дисперсійного аналізу з різними розмірами вибірки:

(1) Знижена статистична потужність.

(2) Надійність зменшена до нерівної дисперсії.

У наступних розділах докладно пояснюється ці дві потенційні проблеми.

Проблема №1: Знижена статистична потужність

Коли ми використовуємо будь-який тип статистичного тесту для порівняння груп, статистична потужність тесту є найвищою, коли кожна група має однаковий розмір вибірки.

Нагадаємо, що статистична потужність стосується ймовірності того, що тест виявляє ефект, коли він насправді існує.

Можна показати, що чим більша різниця у розмірі вибірки між групами, тим нижча статистична потужність ANOVA.

Ось чому дослідники зазвичай хочуть однакові розміри вибірки, щоб мати вищу потужність і, отже, більшу ймовірність виявлення справжніх відмінностей.

Звичайно, можна виконати односторонній ANOVA з різними розмірами вибірки, але ви повинні знати, що потужність одностороннього ANOVA буде зменшена.

Проблема №2: Надійність зменшена до нерівної дисперсії

Одне з припущень одностороннього дисперсійного аналізу полягає в тому, що дисперсія між кожною групою однакова.

Загалом, односторонній дисперсійний аналіз вважається стійким до порушень припущення рівних дисперсій, але лише якщо кожна група має однаковий розмір вибірки .

Отже, якщо у вас є неоднакові розміри вибірки та неоднакові дисперсії між групами, тоді результатам одностороннього дисперсійного аналізу може бути важко довіряти.

Як вирішити, чи використовувати односторонній дисперсійний аналіз із різними розмірами вибірки

Якщо у вас є різні розміри вибірки та ви хочете виконати односторонній дисперсійний аналіз, щоб перевірити відмінності між груповими середніми значеннями, ви можете скористатися наведеною нижче блок-схемою, щоб вирішити, як діяти далі:

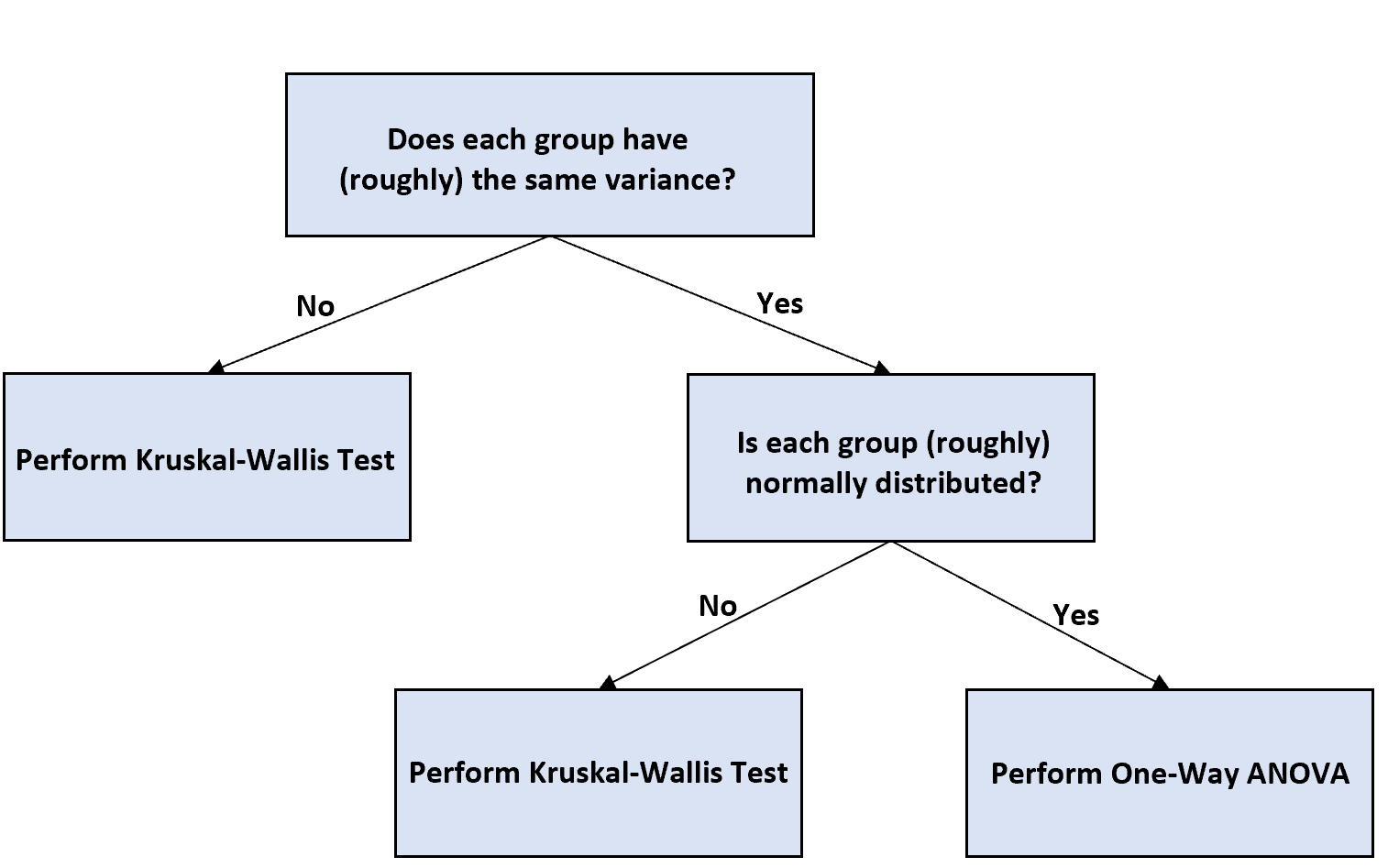
Ось коротке пояснення блок-схеми:

Крок 1: Визначте, чи кожна група має однакову дисперсію.

Щоб визначити, чи кожна група має однакову дисперсію, можна використати один із двох підходів:

• Створіть коробкові діаграми для кожної групи та подивіться, чи приблизно рівний розподіл значень у кожній групі.
• Виконайте формальний статистичний тест для однакових дисперсій, наприклад , тест Бартлетта .

Якщо дисперсії не рівні, виконайте тест Крускала-Уолліса , який вважається непараметричним еквівалентом одностороннього дисперсійного аналізу.

Якщо проміжки рівні, переходимо до наступного кроку.

Крок 2: Визначте, чи кожна група розподілена нормально.

Щоб визначити, чи приблизно нормально розподілені значення в кожній групі, можна використовувати один з двох підходів:

• Створіть гістограми або графіки QQ для кожної групи.
• Виконайте формальні статистичні тести, наприклад Шапіро-Вілка, Колмогорова-Смиронова, Жарка-Барре або Д’Агостіно-Пірсона.

Якщо кожна група розподілена нормально, ви можете провести односторонній дисперсійний аналіз та інтерпретувати результати, як і будь-який звичайний односторонній дисперсійний аналіз.

Якщо кожна група розподілена неправильно, замість цього виконайте тест Крускала-Уолліса.

Додаткові ресурси

Вступ до одностороннього дисперсійного аналізу
Як перевірити припущення ANOVA
Знайомство з тестом Крускала-Уолліса
Як інтерпретувати значення F і P у ANOVA