Як вручну виконати повторний аналіз anova
Дисперсійний аналіз із повторними вимірюваннями використовується для визначення того, чи існує статистично значуща різниця між середніми значеннями трьох або більше груп, у кожній з яких є ті самі суб’єкти.
У цьому підручнику пояснюється, як вручну виконати односторонній повторний аналіз ANOVA.
Приклад: односторонній повторний вимірювання ANOVA вручну
Дослідники хочуть знати, чи викликають три різні препарати різний час реакції. Щоб перевірити це, вони вимірюють час реакції (у секундах) п’яти пацієнтів на кожен препарат. Результати наведені нижче:
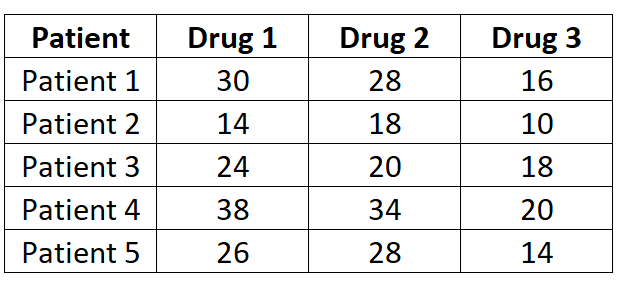
Оскільки кожен пацієнт вимірюється на кожному з трьох препаратів, ми будемо використовувати односторонній повторний аналіз ANOVA, щоб визначити, чи відрізняється середній час реакції між препаратами.
Виконайте наступні кроки, щоб вручну виконати повторні вимірювання ANOVA:
Крок 1: обчисліть SST.
Спочатку ми обчислимо загальну суму квадратів (SST), яку можна знайти за такою формулою:
SST = s 2 всього (n всього -1)
золото:
- s 2 total : дисперсія для набору даних
- n total : загальна кількість спостережень у наборі даних
У цьому прикладі ми обчислюємо SST таким чином: (64,2667)(15-1) = 899,7
Крок 2: Обчисліть SSB
Далі обчислимо суму квадратів (SSB), яку можна знайти за такою формулою:
SSB = Σn j ( x j – x всього ) 2
золото:
- Σ : грецький символ, що означає «сума»
- n j : загальна кількість спостережень у j- й групі
- x j : середнє значення j-ї групи
- x total : середнє значення всіх даних
У цьому прикладі ми обчислюємо SSB таким чином: (5)(26,4-22,533) 2 +(5)(25,6-22,533) 2 + (5)(15,6-22,533) 2 = 362,1
Крок 3: обчисліть SSS.
Далі ми обчислимо предметну суму квадратів (SSS), яку можна знайти за такою формулою:
SSS =(Σr 2 k /c) – (N 2 /rc)
золото:
- Σ : грецький символ, що означає «сума»
- r 2 k : квадрат суми k-го пацієнта
- N: загальна сума всіх даних
- r: загальна кількість пацієнтів
- c: загальна кількість груп
У цьому прикладі ми обчислюємо SSS таким чином: ((74 2 + 42 2 + 62 2 + 92 2 + 68 2 )/3) – (338 2 /(5)(3)) = 441,1
Крок 4: розрахувати SES.
Далі ми обчислимо суму квадратів похибок (SSE), яку можна знайти за такою формулою:
SSE = SST – SSB – SSS
У цьому прикладі ми розраховуємо SES так: 899,7 – 362,1 – 441,1 = 96,5
Крок 5: Заповніть таблицю ANOVA для повторних вимірювань.
Тепер, коли у нас є SSB, SSS і SSE, ми можемо заповнити таблицю повторних вимірювань ANOVA:
| Джерело | Сума квадратів (SS) | df | Середні квадрати (MS) | Ф |
|---|---|---|---|---|
| Між | 362.1 | 2 | 181.1 | 15,006 |
| Тема | 441.1 | 4 | 110.3 | |
| Помилка | 96.5 | 8 | 12.1 |
Ось як ми розрахували різні числа в таблиці:
- df між: #groups – 1 = 3 – 1 = 2
- Тема df: #учасники – 1 = 5 – 1 = 4
- Помилка df: df між * df тема = 2*4 = 8
- MS входить: SSB / df входить = 362,1 / 2 = 181,1
- MS суб’єкт: SSS суб’єкт / df = 441,1 / 4 = 110,3
- Помилка MS: помилка SSE / df = 96,5 / 8 = 12,1
- F: MS входить / MS error = 181,1 / 12,1 = 15,006
Крок 6: Інтерпретація результатів.
Статистика F-тесту для цього одностороннього повторного вимірювання ANOVA становить 15,006 . Щоб визначити, чи є це статистично значущим результатом, нам потрібно порівняти його з критичним значенням F, знайденим у таблиці розподілу F із такими значеннями:
- α (рівень значущості) = 0,05
- DF1 (ступені свободи чисельника) = df між = 2
- DF2 (ступені свободи знаменника) = помилка df = 8
Ми знаходимо, що критичне значення F становить 4,459 .
Оскільки F тестова статистика в таблиці ANOVA більша за критичне значення F у таблиці F розподілу, ми відхиляємо нульову гіпотезу. Це означає, що ми маємо достатньо доказів, щоб стверджувати, що існує статистично значуща різниця між середнім часом реакції на ліки.