Anova проти регресії: у чому різниця?
Дві моделі, які найчастіше використовуються в статистиці, — це дисперсійний аналіз і регресійна модель.
Ці два типи моделей мають наступну схожість:
- Змінна відповіді в кожній моделі є постійною. Приклади безперервних змінних включають вагу, зріст, довжину, ширину, час, вік тощо.
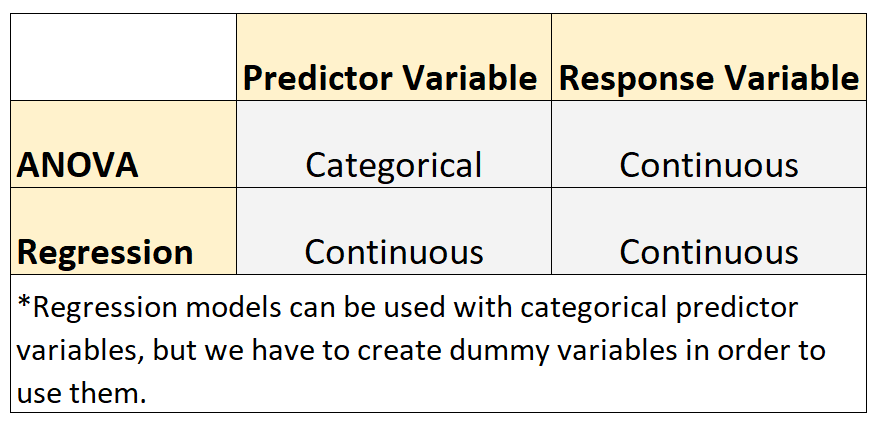
Однак ці два типи моделей мають такі відмінності :
- Моделі ANOVA використовуються, коли прогностичні змінні є категоричними. Приклади категоріальних змінних включають рівень освіти, колір очей, сімейний стан тощо.
- Регресійні моделі використовуються, коли прогностичні змінні неперервні.*
*Моделі регресії можна використовувати з категоріальними змінними предикторів, але для їх використання потрібно створити фіктивні змінні .
Наведені нижче приклади показують, коли використовувати ANOVA або регресійні моделі на практиці.
Приклад 1: Бажана модель ANOVA
Припустімо, біолог хоче зрозуміти, чи призводять чотири різні добрива до однакового середнього росту рослин (у дюймах) протягом одного місяця. Щоб перевірити це, вона застосовує кожне добриво до 20 рослин і реєструє ріст кожної рослини через місяць.
У цьому сценарії біолог повинен використовувати односторонню модель дисперсійного аналізу, щоб проаналізувати відмінності між добривами, оскільки існує змінна предиктора, і вона є категоричною.
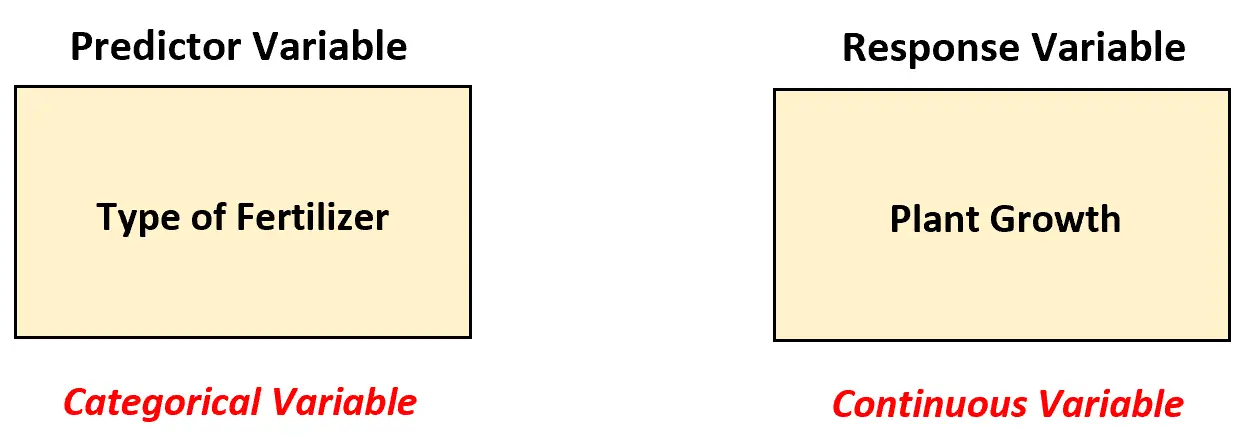
Іншими словами, значення змінної предиктора можна класифікувати за наступними «категоріями»:
- Добриво 1
- Добриво 2
- Добриво 3
- Добриво 4
Односторонній ANOVA скаже біологу, чи є середній ріст рослин однаковим для чотирьох різних добрив.
Приклад 2: Бажана модель регресії
Скажімо, агент з нерухомості хоче зрозуміти зв’язок між квадратними метрами та ціною нерухомості. Щоб проаналізувати цю залежність, він збирає дані про квадратні метри та ціни 200 будинків у конкретному місті.
У цьому сценарії агент з нерухомості повинен використовувати просту лінійну регресійну модель для аналізу зв’язку між цими двома змінними, оскільки змінна-прогноз (квадратний фут) є постійною.
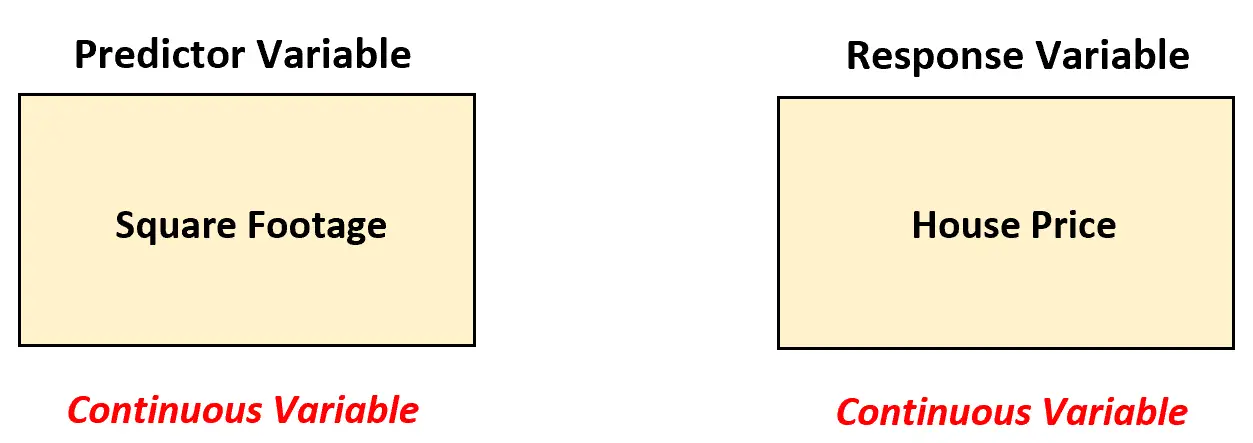
Використовуючи просту лінійну регресію, агент з нерухомості може підібрати таку модель регресії:
Ціна нерухомості = β 0 + β 1 (квадратна площа)
Значення β 1 представлятиме середню зміну ціни будинку, пов’язану з кожним додатковим квадратним футом.
Це дозволить агенту з нерухомості кількісно визначити співвідношення між квадратними метрами та ціною нерухомості.
Приклад 3: регресійна модель із бажаними фіктивними змінними
Припустімо, що агент з нерухомості хоче зрозуміти зв’язок між змінними прогнозу «квадратний фут» і «тип будинку» (одна сім’я, квартира, таунхаус) зі змінною відповіді ціни нерухомості.
У цьому сценарії агент з нерухомості може використовувати множинну лінійну регресію, перетворюючи «тип будинку» на фіктивну змінну, оскільки наразі це категоріальна змінна.
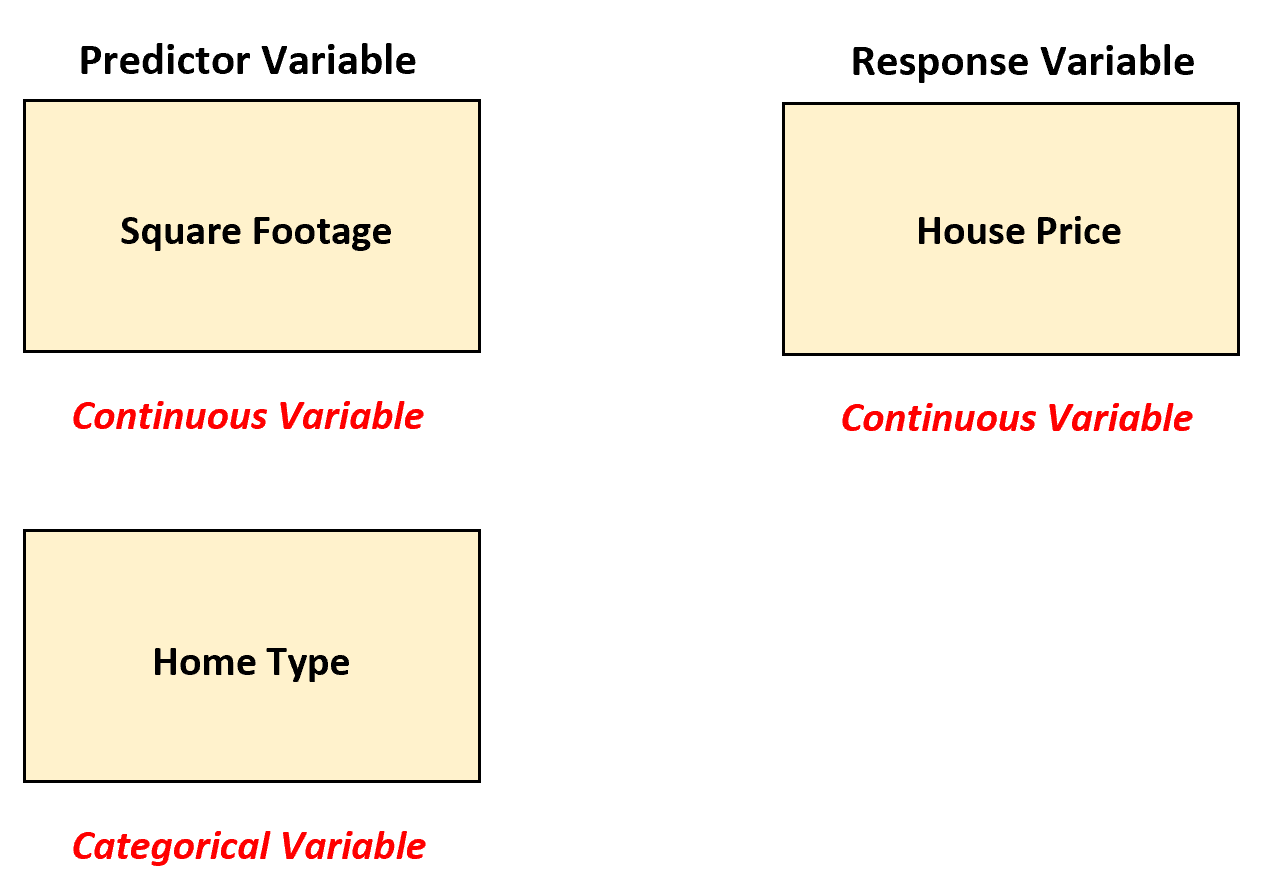
Тоді агент з нерухомості може підібрати наступну модель множинної лінійної регресії:
Ціна нерухомості = β 0 + β 1 (площа) + β 2 (одна сім’я) + β 3 (квартира)
Ось як ми будемо інтерпретувати коефіцієнти моделі:
- β 1 : Середня зміна ціни будинку, пов’язана з одним додатковим квадратним футом.
- β 2 : Середня різниця в ціні між односімейним будинком і таунхаусом, припускаючи, що площа квадратних метрів залишається незмінною.
- β 3 : Середня різниця в ціні між односімейним будинком і квартирою, припускаючи постійну площу.
Перегляньте наступні навчальні посібники, щоб дізнатися, як створювати фіктивні змінні в різних статистичних програмах:
Додаткові ресурси
Наступні навчальні посібники містять поглиблений вступ до моделей ANOVA:
Наступні навчальні посібники містять поглиблений вступ до моделей лінійної регресії:
Про автора
Редакція
Привіт, я Бенджамін, професор статистики на пенсії, який став викладачем статистики. Маючи великий досвід і знання в галузі статистики, я готовий поділитися своїми знаннями, щоб розширити можливості студентів через Statorials. Дізнайтеся більше