Binompdf проти binomcdf: різниця (плюс приклади)
Біноміальний розподіл є одним із найбільш часто використовуваних розподілів у всій статистиці.
На калькуляторі TI-84 ви можете використовувати дві функції, щоб знайти ймовірності, пов’язані з біноміальним розподілом:
- binompdf(n, p, x) : знаходить імовірність того, що рівно x успіхів буде досягнуто протягом n випробувань, де ймовірність успіху в даному випробуванні дорівнює p .
- binomcdf(n, p, x) : знаходить ймовірність того, що x або менше успіхів відбувається протягом n випробувань, де ймовірність успіху в даному випробуванні дорівнює p .
Ви можете отримати доступ до кожної з цих функцій на калькуляторі TI-84, натиснувши 2nd, а потім натиснувши VARS . Це приведе вас до екрана DISTR , де ви зможете використовувати binompdf() і binomcdf() :
Наступні приклади показують, як використовувати кожну з цих функцій на практиці.
Приклади: як використовувати Binompdf()
У наступних прикладах показано, як використовувати функцію binompdf() .
Приклад 1: Штрафні кидки
Джессіка виконує 80% своїх штрафних кидків. Якщо вона виконує 10 штрафних кидків, яка ймовірність того, що вона зробить рівно 7?
Щоб відповісти на це питання, ми можемо ввести наступну формулу:
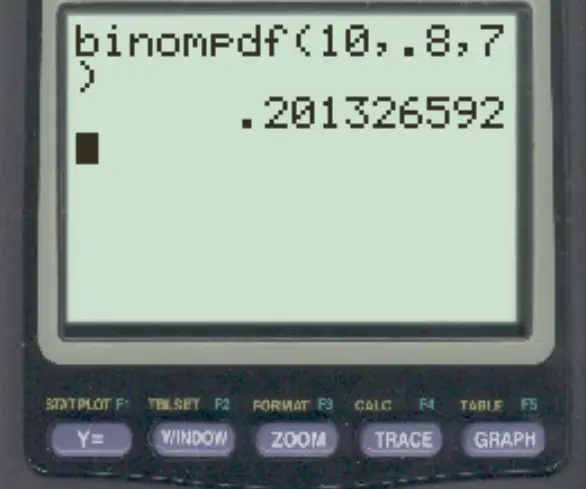
Імовірність того, що вона отримає рівно 7, дорівнює 0,2013 .
Приклад 2: Шахрайські операції
Банк знає, що 3% усіх операцій є шахрайськими. Якщо в один день відбувається 20 транзакцій, яка ймовірність того, що саме 2 є шахрайськими?
Щоб відповісти на це питання, ми можемо ввести наступну формулу:
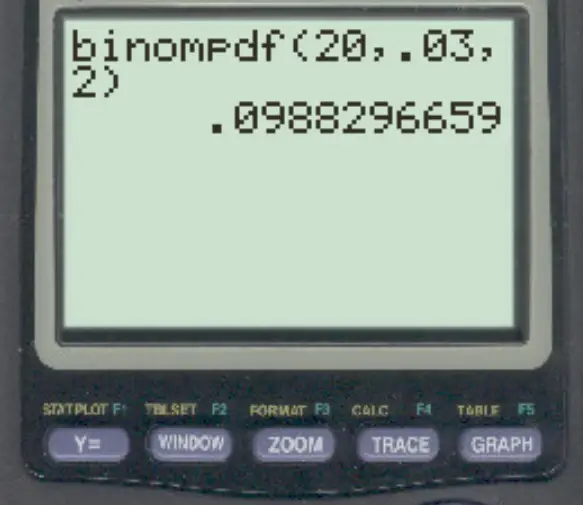
Імовірність того, що рівно 2 транзакції є шахрайськими, становить 0,0988 .
Приклади: як використовувати Binomcdf()
У наступних прикладах показано, як використовувати функцію binomcdf() .
Приклад 1: Штрафні кидки
Джессіка виконує 50% своїх штрафних кидків. Якщо вона виконує 10 штрафних кидків, яка ймовірність того, що вона зробить 7 або менше?
Щоб відповісти на це питання, ми можемо ввести наступну формулу:
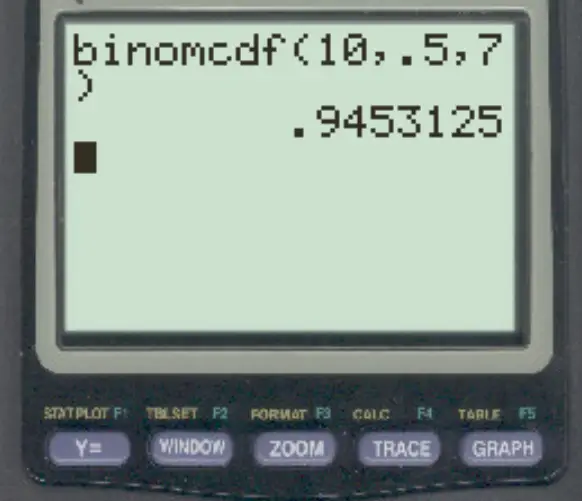
Імовірність того, що вона зробить 7 або менше штрафних кидків, становить 0,9453 .
Приклад 2: Шахрайські операції
Банк знає, що 3% усіх операцій є шахрайськими. Якщо в один день відбувається 20 транзакцій, яка ймовірність того, що більше ніж 2 транзакції є шахрайськими?
Щоб відповісти на це питання, ми можемо ввести наступну формулу:
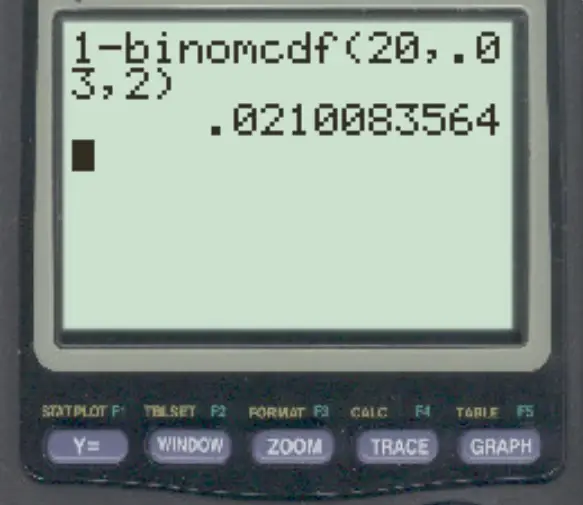
Імовірність того, що більше 2 транзакцій є шахрайськими, становить 0,021 .
Додаткові ресурси
Калькулятор біноміального розподілу
Як виконати біноміальний тест в Excel