Як виконати корекцію бонферроні в r

Односторонній дисперсійний аналіз використовується, щоб визначити, чи існує статистично значуща різниця між середніми значеннями трьох або більше незалежних груп.

Якщо загальне p-значення таблиці ANOVA нижче певного рівня значущості, тоді ми маємо достатньо доказів, щоб стверджувати, що принаймні одне з групових середніх відрізняється від інших.

Однак це не говорить нам , які групи відрізняються одна від одної. Це просто говорить нам про те, що не всі середні групові показники однакові.

Щоб точно знати, які групи відрізняються одна від одної, нам потрібно виконати попарні t-тести між кожною групою, контролюючи частоту помилок для сімейства .

Одним із найпоширеніших способів досягти цього є використання поправки Бонферроні при обчисленні p-значень для кожного з попарних t-тестів.

У цьому посібнику пояснюється, як виконати корекцію Бонферроні в R.

Приклад: поправка Бонферроні в R

Припустімо, що вчитель хоче знати, чи призводять три різні методи навчання до різних результатів тестів серед учнів.

Щоб перевірити це, вона випадковим чином призначає 10 студентів для використання кожної методики навчання. Після тижня використання призначеної методики навчання кожен студент складає той самий іспит.

Ми можемо використати наступні кроки в R, щоб підібрати односторонній дисперсійний аналіз і використати поправку Бонферроні, щоб обчислити попарні відмінності між результатами іспитів кожної групи.

Крок 1: Створіть набір даних.

Наступний код показує, як створити набір даних, що містить результати іспитів усіх 30 студентів:

 #create data frame
data <- data.frame(technique = rep (c("tech1", "tech2", "tech3"), each = 10 ),
                   score = c(76, 77, 77, 81, 82, 82, 83, 84, 85, 89,
                             81, 82, 83, 83, 83, 84, 87, 90, 92, 93,
                             77, 78, 79, 88, 89, 90, 91, 95, 95, 98))

#view first six rows of data frame
head(data)

  technical score
1 tech1 76
2 tech1 77
3 tech1 77
4 tech1 81
5 tech1 82
6 tech1 82

Крок 2: Перегляньте результати іспиту для кожної групи.

У наведеному нижче коді показано, як створити коробкові діаграми для візуалізації розподілу результатів іспитів для кожної групи:

 boxplot(score ~ technique,
        data = data,
        main = "Exam Scores by Studying Technique",
        xlab = "Studying Technique",
        ylab = "Exam Scores",
        col = "steelblue",
        border = "black")

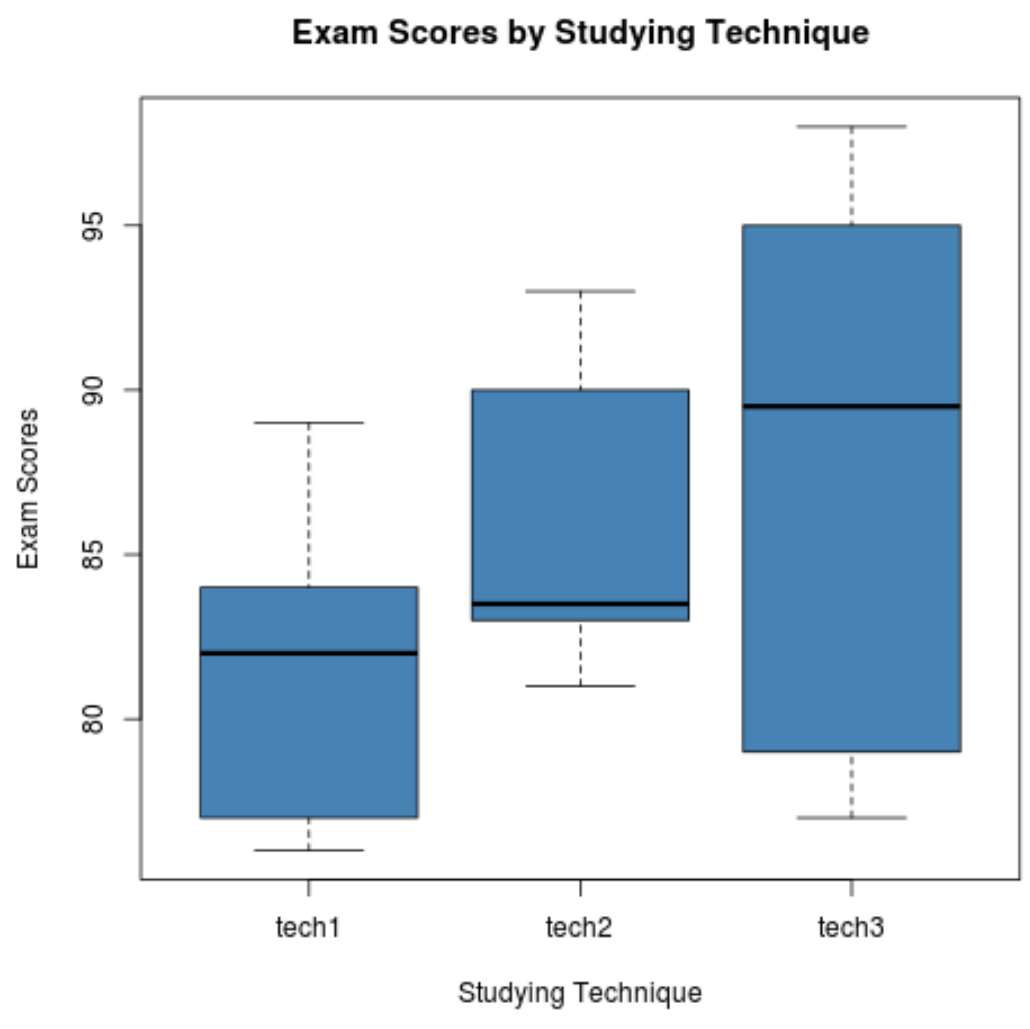
Крок 3: Виконайте односторонній дисперсійний аналіз.

У наведеному нижче коді показано, як виконати односторонній дисперсійний аналіз, щоб перевірити різницю між середніми оцінками іспиту в кожній групі:

 #fit the one-way ANOVA model
model <- aov(score ~ technique, data = data)

#view model output
summary(model)

            Df Sum Sq Mean Sq F value Pr(>F)  
technical 2 211.5 105.73 3.415 0.0476 *
Residuals 27 836.0 30.96                 
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Оскільки загальне значення p ( 0,0476 ) менше 0,05, це означає, що кожна група не має однакового середнього балу за іспит.

Далі ми виконаємо попарні t-тести, використовуючи поправку Бонферроні для p-значень, щоб обчислити попарні різниці між результатами іспитів кожної групи.

Крок 4: Виконайте попарні t-тести.

Щоб виконати попарні t-тести з корекцією Бонферроні в R, ми можемо використати функцію pairwise.t.test() , яка використовує такий синтаксис:

pairwise.t.test(x, g, p.adjust.method=”bonferroni”)

золото:

• x: числовий вектор значень відповіді
• g: вектор, що вказує назви груп (наприклад, метод дослідження)

Наступний код показує, як використовувати цю функцію для нашого прикладу:

 #perform pairwise t-tests with Bonferroni's correction
pairwise.t.test(data$score, data$technique, p.adjust.method=" bonferroni ")

	Pairwise comparisons using t tests with pooled SD 

data: data$score and data$technique 

      tech1 tech2
tech2 0.309 -    
tech3 0.048 1.000

P value adjustment method: bonferroni

Спосіб інтерпретації результату такий:

• Скоригований p-значення для середньої різниці в результатах іспиту між технікою 1 і технікою 2 становить 0,309 .
• Скоригований p-значення для середньої різниці в результатах іспиту між технікою 1 і технікою 3 становить 0,048 .
• Скориговане значення p для середньої різниці в результатах іспиту між технікою 2 і технікою 3 становить 1000 .

Виходячи з результатів, ми бачимо, що єдина істотна різниця між технікою 1 і технікою 3.

Додаткові ресурси

Вступ до одностороннього дисперсійного аналізу
Як виконати односторонній дисперсійний аналіз у R
Як виконати тест Тьюкі в R
Як виконати тест Даннетта в R