Як виконати завантаження в r (з прикладами)

Бутстрапінг — це метод, який можна використовувати для оцінки стандартної помилки будь-якої статистики та отримання довірчого інтервалу для статистики.

Основний процес початкового завантаження виглядає наступним чином:

• Візьміть k повторних зразків із заміною з заданого набору даних.
• Для кожного зразка обчисліть цікаву статистику.
• Це дає k різних оцінок для заданої статистики, які потім можна використовувати для обчислення стандартної помилки статистики та створення довірчого інтервалу для статистики.

Ми можемо виконати початкове завантаження в R, використовуючи такі функції з бібліотеки початкового завантаження :

1. Згенеруйте зразки початкового завантаження.

завантаження (дані, статистика, R, …)

золото:

• дані: вектор, матриця або блок даних
• statistic: функція, яка створює статистичні дані, які потрібно ініціювати
• A: Кількість повторів початкового завантаження

2. Створіть початковий довірчий інтервал.

boot.ci(об’єкт завантаження, conf, тип)

золото:

• bootobject: об’єкт, що повертається функцією boot().
• conf: довірчий інтервал для обчислення. Значення за замовчуванням 0,95
• тип: Тип довірчого інтервалу для обчислення. Параметри включають «стандартний», «базовий», «стад», «perc», «bca» та «усі» – за умовчанням встановлено «усі»

Наступні приклади показують, як використовувати ці функції на практиці.

Приклад 1: завантажте одну статистику

У наведеному нижче коді показано, як обчислити стандартну помилку для R-квадрата моделі простої лінійної регресії:

 set.seed(0)
library (boot)

#define function to calculate R-squared
rsq_function <- function (formula, data, indices) {
  d <- data[indices,] #allows boot to select sample
  fit <- lm(formula, data=d) #fit regression model
  return (summary(fit)$r.square) #return R-squared of model
}
#perform bootstrapping with 2000 replications
reps <- boot(data=mtcars, statistic=rsq_function, R=2000, formula=mpg~disp)

#view results of boostrapping
reps

ORDINARY NONPARAMETRIC BOOTSTRAP


Call:
boot(data = mtcars, statistic = rsq_function, R = 2000, formula = mpg ~ 
    available)


Bootstrap Statistics:
     original bias std. error
t1* 0.7183433 0.002164339 0.06513426

З результатів ми бачимо:

• Розрахунковий R-квадрат для цієї моделі регресії становить 0,7183433 .
• Стандартна помилка для цієї оцінки становить 0,06513426 .

Ми також можемо швидко візуалізувати розподіл початкових зразків:

 plot(reps)

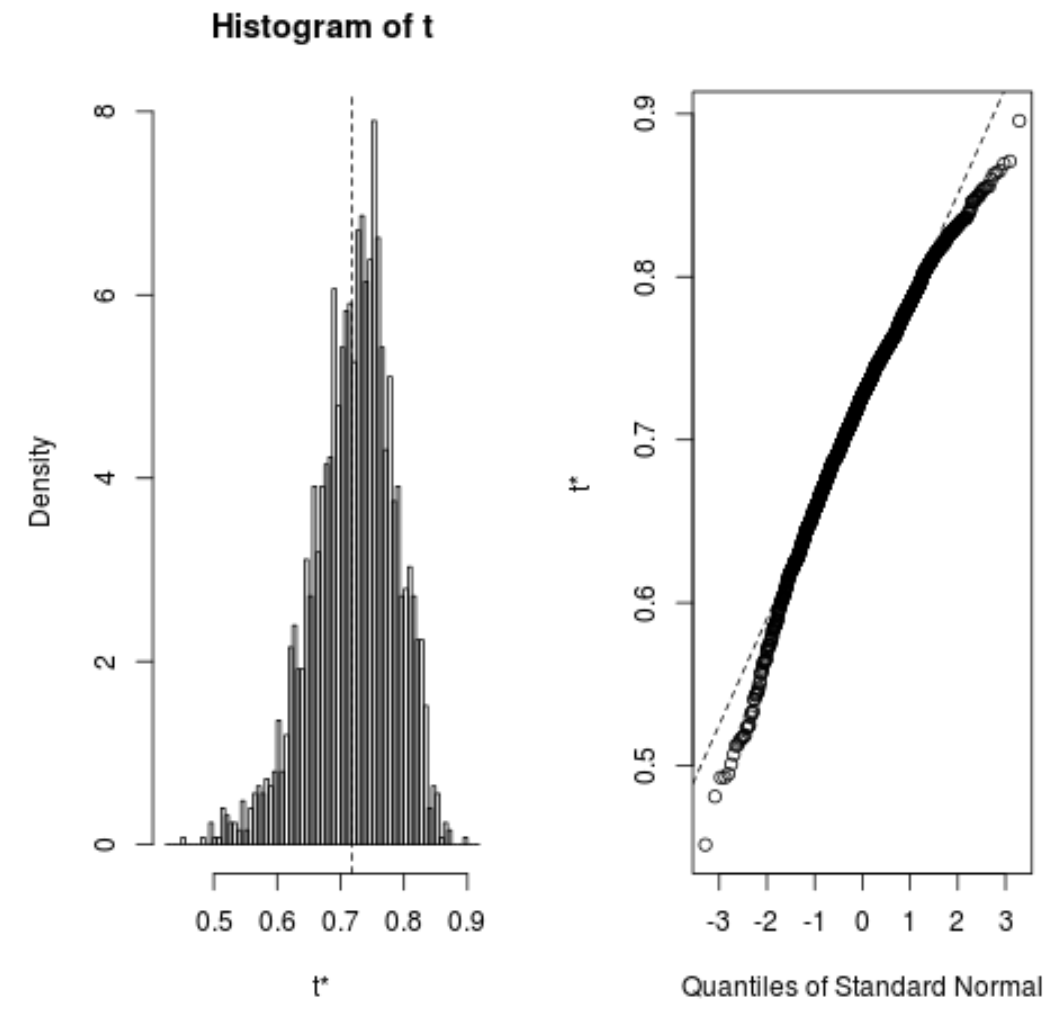
Ми також можемо використати такий код, щоб обчислити 95% довірчий інтервал для оціненого R-квадрата моделі:

 #calculate adjusted bootstrap percentile (BCa) interval
boot.ci(reps, type=" bca ")

CALL: 
boot.ci(boot.out = reps, type = "bca")

Intervals: 
Level BCa          
95% (0.5350, 0.8188)  
Calculations and Intervals on Original Scale

З результату ми бачимо, що початковий 95% довірчий інтервал для справжніх значень R-квадрат становить (0,5350, 0,8188).

Приклад 2: початкове завантаження кількох статистичних даних

У наступному коді показано, як обчислити стандартну помилку для кожного коефіцієнта в моделі множинної лінійної регресії:

 set.seed(0)
library (boot)

#define function to calculate fitted regression coefficients
coef_function <- function (formula, data, indices) {
  d <- data[indices,] #allows boot to select sample
  fit <- lm(formula, data=d) #fit regression model
  return (coef(fit)) #return coefficient estimates of model
}

#perform bootstrapping with 2000 replications
reps <- boot(data=mtcars, statistic=coef_function, R=2000, formula=mpg~disp)

#view results of boostrapping
reps

ORDINARY NONPARAMETRIC BOOTSTRAP


Call:
boot(data = mtcars, statistic = coef_function, R = 2000, formula = mpg ~ 
    available)


Bootstrap Statistics:
       original bias std. error
t1* 29.59985476 -5.058601e-02 1.49354577
t2* -0.04121512 6.549384e-05 0.00527082

З результатів ми бачимо:

• Розрахунковий коефіцієнт для перетину моделі становить 29,59985476 , а стандартна помилка цієї оцінки становить 1,49354577 .
• Оцінений коефіцієнт для змінної предиктора disp у моделі становить -0,04121512 , а стандартна помилка цієї оцінки становить 0,00527082 .

Ми також можемо швидко візуалізувати розподіл початкових зразків:

 plot(reps, index=1) #intercept of model
plot(reps, index=2) #disp predictor variable

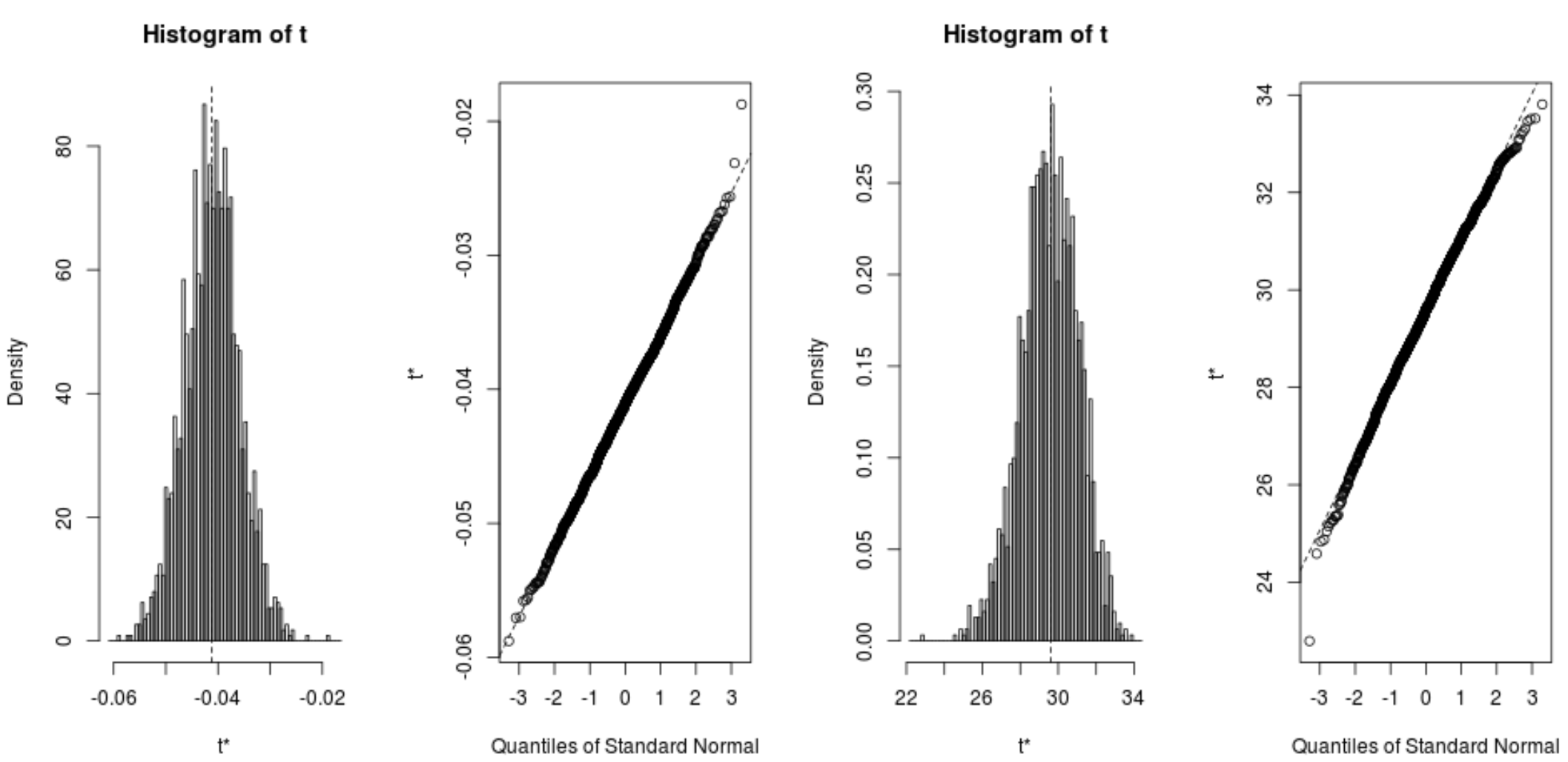
Ми також можемо використати такий код, щоб обчислити 95% довірчі інтервали для кожного коефіцієнта:

 #calculate adjusted bootstrap percentile (BCa) intervals
boot.ci(reps, type=" bca ", index=1) #intercept of model
boot.ci(reps, type=" bca ", index=2) #disp predictor variable

CALL: 
boot.ci(boot.out = reps, type = "bca", index = 1)

Intervals: 
Level BCa          
95% (26.78, 32.66)  
Calculations and Intervals on Original Scale
BOOTSTRAP CONFIDENCE INTERVAL CALCULATIONS
Based on 2000 bootstrap replicates

CALL: 
boot.ci(boot.out = reps, type = "bca", index = 2)

Intervals: 
Level BCa          
95% (-0.0520, -0.0312)  
Calculations and Intervals on Original Scale

З результатів ми бачимо, що початкові 95% довірчі інтервали для коефіцієнтів моделі такі:

• IC для перехоплення: (26.78, 32.66)
• CI для відображення : (-.0520, -.0312)

Додаткові ресурси

Як виконати просту лінійну регресію в R
Як виконати множинну лінійну регресію в R
Вступ до довірчих інтервалів