Як виконати перетворення бокса-кокса в python

Перетворення боксу-Кокса є широко використовуваним методом для перетворення ненормально розподіленого набору даних у більш нормально розподілений набір.

Основна ідея цього методу полягає в тому, щоб знайти таке значення для λ, щоб перетворені дані були якнайближчими до нормального розподілу, використовуючи таку формулу:

• y(λ) = (y ^λ – 1) / λ, якщо y ≠ 0
• y(λ) = log(y), якщо y = 0

Ми можемо виконати перетворення box-cox у Python за допомогою функції scipy.stats.boxcox() .

У наступному прикладі показано, як використовувати цю функцію на практиці.

Приклад: перетворення Бокса-Кокса в Python

Припустимо, ми генеруємо випадковий набір із 1000 значень з експоненціального розподілу :

 #load necessary packages
import numpy as np 
from scipy. stats import boxcox 
import seaborn as sns 

#make this example reproducible
n.p. random . seeds (0)

#generate dataset
data = np. random . exponential (size= 1000 )

#plot the distribution of data values
sns. distplot (data, hist= False , kde= True ) 

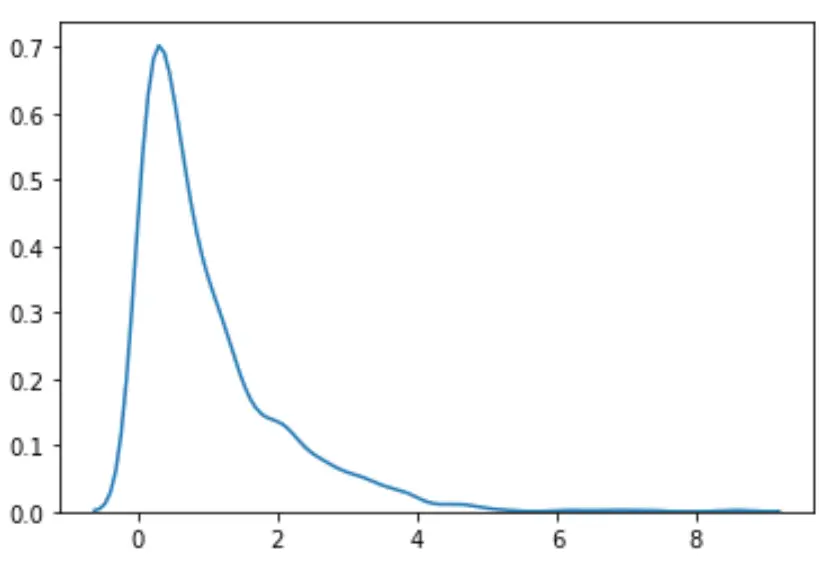
Ми бачимо, що розподіл не здається нормальним.

Ми можемо використати функцію boxcox() , щоб знайти оптимальне значення лямбда, яке дає більш нормальний розподіл:

 #perform Box-Cox transformation on original data
transformed_data, best_lambda = boxcox(data) 

#plot the distribution of the transformed data values
sns. distplot (transformed_data, hist= False , kde= True ) 

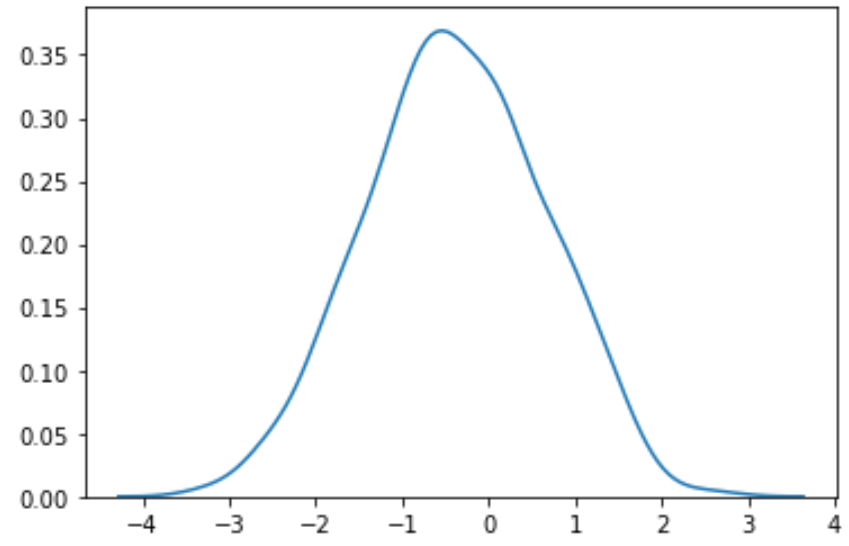
Ми бачимо, що перетворені дані мають набагато більш нормальний розподіл.

Ми також можемо знайти точне значення лямбда, яке використовується для виконання перетворення Бокса-Кокса:

 #display optimal lambda value
print (best_lambda)

0.2420131978174143

Виявлено, що оптимальна лямбда становить близько 0,242 .

Таким чином, кожне значення даних було перетворено за допомогою наступного рівняння:

Новий = (старий ^0,242 – 1) / 0,242

Ми можемо підтвердити це, подивившись значення вихідних даних у порівнянні з перетвореними даними:

 #view first five values of original dataset
data[0:5]

array([0.79587451, 1.25593076, 0.92322315, 0.78720115, 0.55104849])

#view first five values of transformed dataset
transformed_data[0:5]

array([-0.22212062, 0.23427768, -0.07911706, -0.23247555, -0.55495228])

Перше значення в оригінальному наборі даних було 0,79587 . Отже, ми застосували наступну формулу для перетворення цього значення:

Нове = (0,79587 ^0,242 – 1) / 0,242 = -0,222

Ми можемо підтвердити, що перше значення в перетвореному наборі даних справді дорівнює -0,222 .

Додаткові ресурси

Як створити та інтерпретувати графік QQ у Python
Як виконати тест нормальності Шапіро-Вілка в Python