Як виконати перетворення бокса-кокса в r (з прикладами)

Перетворення боксу-Кокса є широко використовуваним методом для перетворення ненормально розподіленого набору даних у більш нормально розподілений набір.

Основна ідея цього методу полягає в тому, щоб знайти таке значення для λ, щоб перетворені дані були якнайближчими до нормального розподілу, використовуючи таку формулу:

• y(λ) = (y ^λ – 1) / λ, якщо y ≠ 0
• y(λ) = log(y), якщо y = 0

Ми можемо виконати перетворення box-cox у R за допомогою функції boxcox() із бібліотеки MASS() . У наступному прикладі показано, як використовувати цю функцію на практиці.

Зверніться до цієї статті Університету Коннектикуту, щоб отримати гарний підсумок розвитку трансформації Бокса-Кокса.

Приклад: перетворення Бокса-Кокса в R

У наведеному нижче коді показано, як адаптувати модель лінійної регресії до набору даних, а потім використовувати функцію boxcox() , щоб знайти оптимальну лямбду для перетворення змінної відповіді та адаптації нової моделі.

 library (MASS)

#create data
y=c(1, 1, 1, 2, 2, 2, 2, 2, 2, 3, 3, 3, 6, 7, 8)
x=c(7, 7, 8, 3, 2, 4, 4, 6, 6, 7, 5, 3, 3, 5, 8)

#fit linear regression model
model <- lm(y~x)

#find optimal lambda for Box-Cox transformation 
bc <- boxcox(y ~ x)
(lambda <- bc$x[which.max(bc$y)])

[1] -0.4242424

#fit new linear regression model using the Box-Cox transformation
new_model <- lm(((y^lambda-1)/lambda) ~ x)

Оптимальна лямбда виявилася -0,4242424 . Таким чином, нова модель регресії замінила вихідну змінну відповіді y на змінну y = (y ^-0,4242424 – 1) / -0,4242424.

У наступному коді показано, як створити два графіки QQ у R, щоб візуалізувати різницю в залишках між двома регресійними моделями:

 #define plotting area
op <- par(pty = "s", mfrow = c(1, 2))

#QQ plot for original model
qqnorm(model$residuals)
qqline(model$residuals)

#QQ plot for Box-Cox transformed model
qqnorm(new_model$residuals)
qqline(new_model$residuals)

#display both QQ plots
by(op)

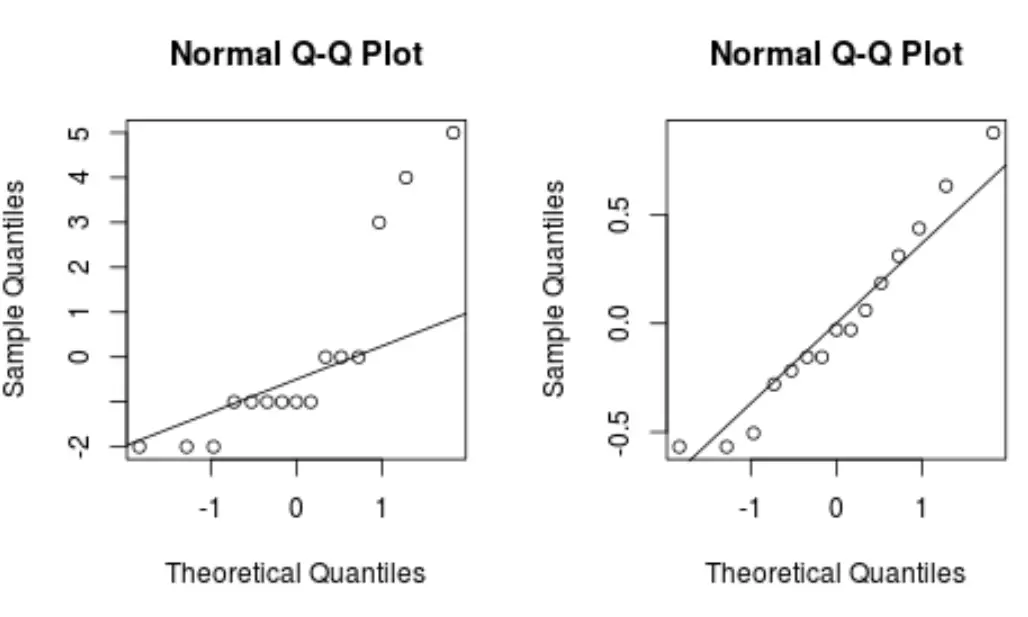
Як правило, якщо точки даних лежать уздовж прямої діагональної лінії на графіку QQ, набір даних, ймовірно, відповідає нормальному розподілу.

Зверніть увагу, як трансформована модель Бокса-Кокса створює графік QQ із набагато більш прямолінійною лінією, ніж оригінальна модель регресії.

Це вказує на те, що залишки трансформованої моделі Бокса-Кокса розподілені набагато більш нормально, що задовольняє одне з припущень лінійної регресії .

Додаткові ресурси

Як перетворити дані в R (логарифм, квадратний корінь, кубічний корінь)
Як створити та інтерпретувати діаграму QQ у R
Як виконати тест Шапіро-Вілка на нормальність у R