Як виконати тест брейша-пагана в excel

Критерій Брейша-Пейгана використовується для визначення наявності гетероскедастичності в регресійному аналізі.

У цьому посібнику пояснюється, як виконати тест Брейша-Пейгана в Excel.

Приклад: тест Брейша-Пагана в Excel

Для цього прикладу ми використаємо наступний набір даних, який описує атрибути 10 баскетболістів.

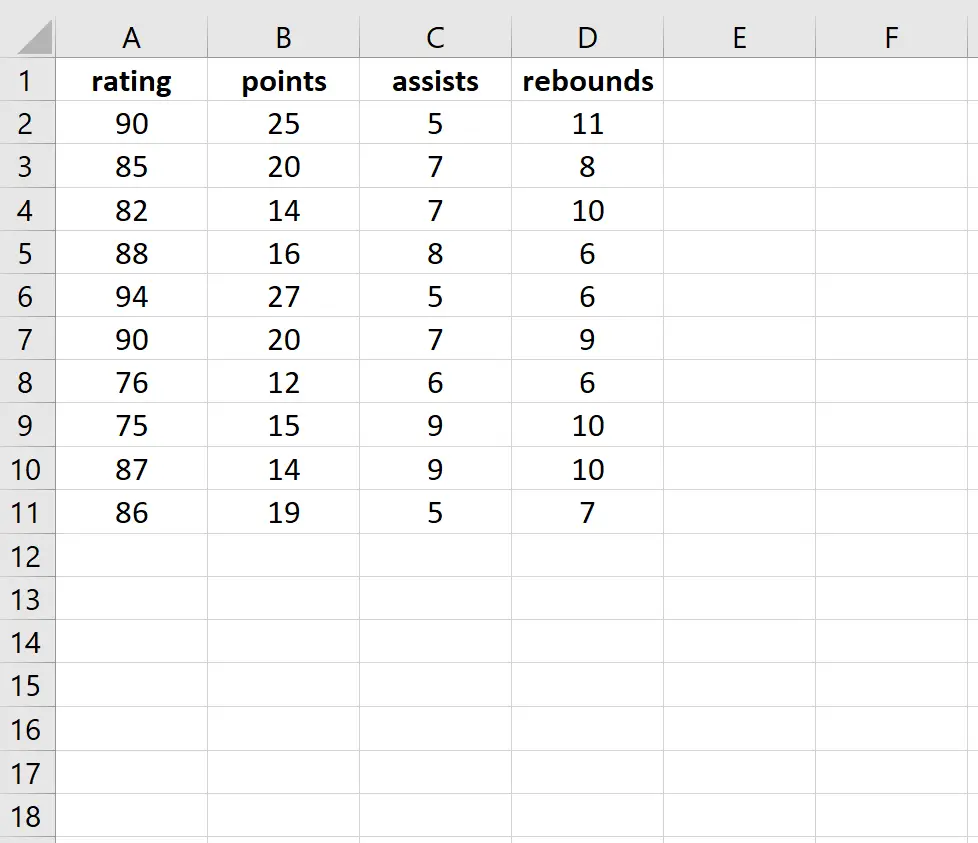
Ми підберемо модель множинної лінійної регресії, використовуючи оцінку як змінну реакції та очки, передачі та підбирання як пояснювальні змінні. Далі ми виконаємо тест Брейша-Пейгана, щоб визначити, чи присутня гетероскедастичність у регресії.

Крок 1: Виконайте множинну лінійну регресію.

На верхній стрічці Excel перейдіть на вкладку «Дані» та натисніть «Аналіз даних». Якщо ви не бачите цей параметр, спершу потрібно інсталювати безкоштовне програмне забезпечення Analysis ToolPak .

Коли ви натиснете «Аналіз даних», з’явиться нове вікно. Виберіть «Регресія» та натисніть «ОК». Заповніть необхідні таблиці для змінних відповіді та пояснювальних змінних, а потім натисніть OK.

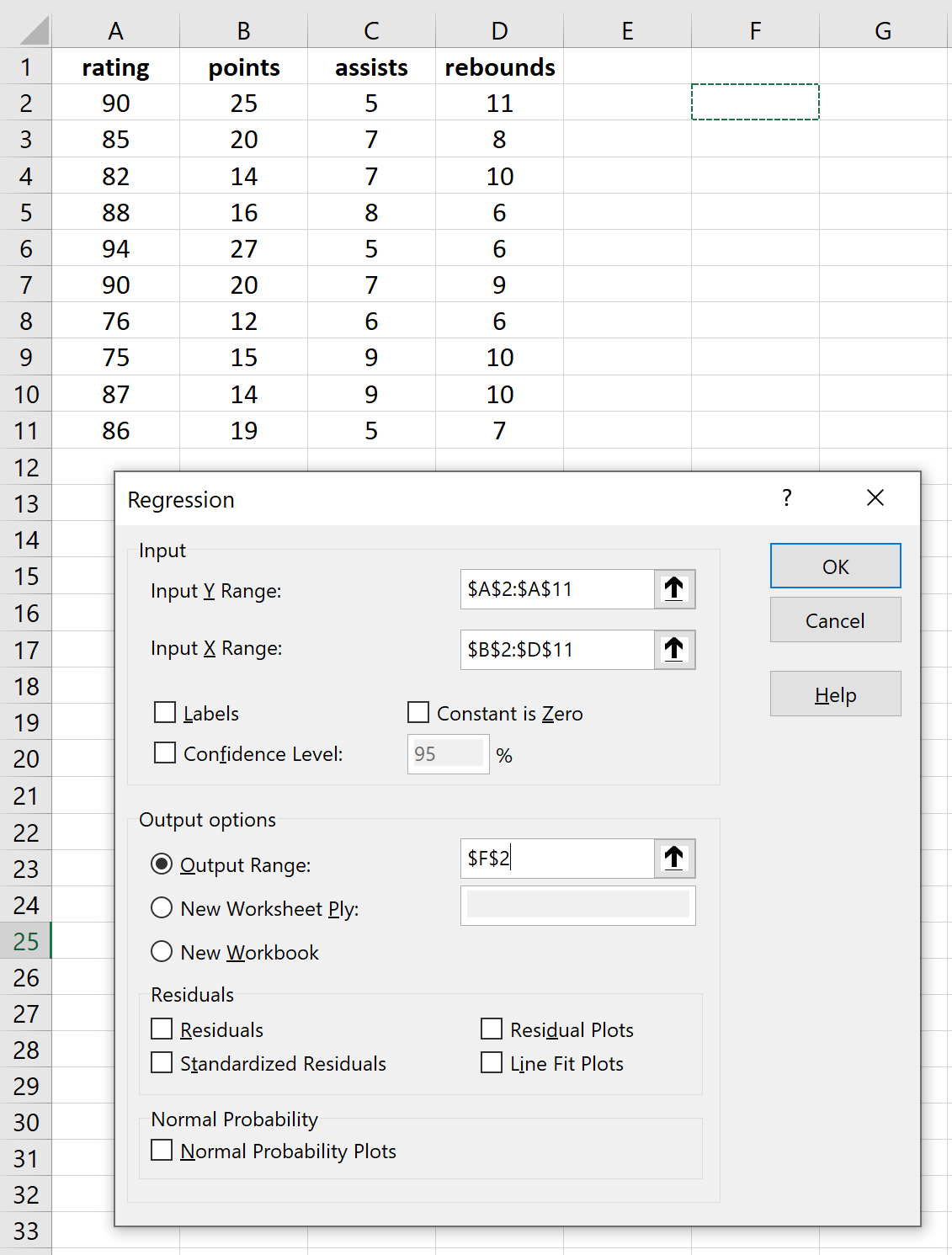
Це дає такий результат:

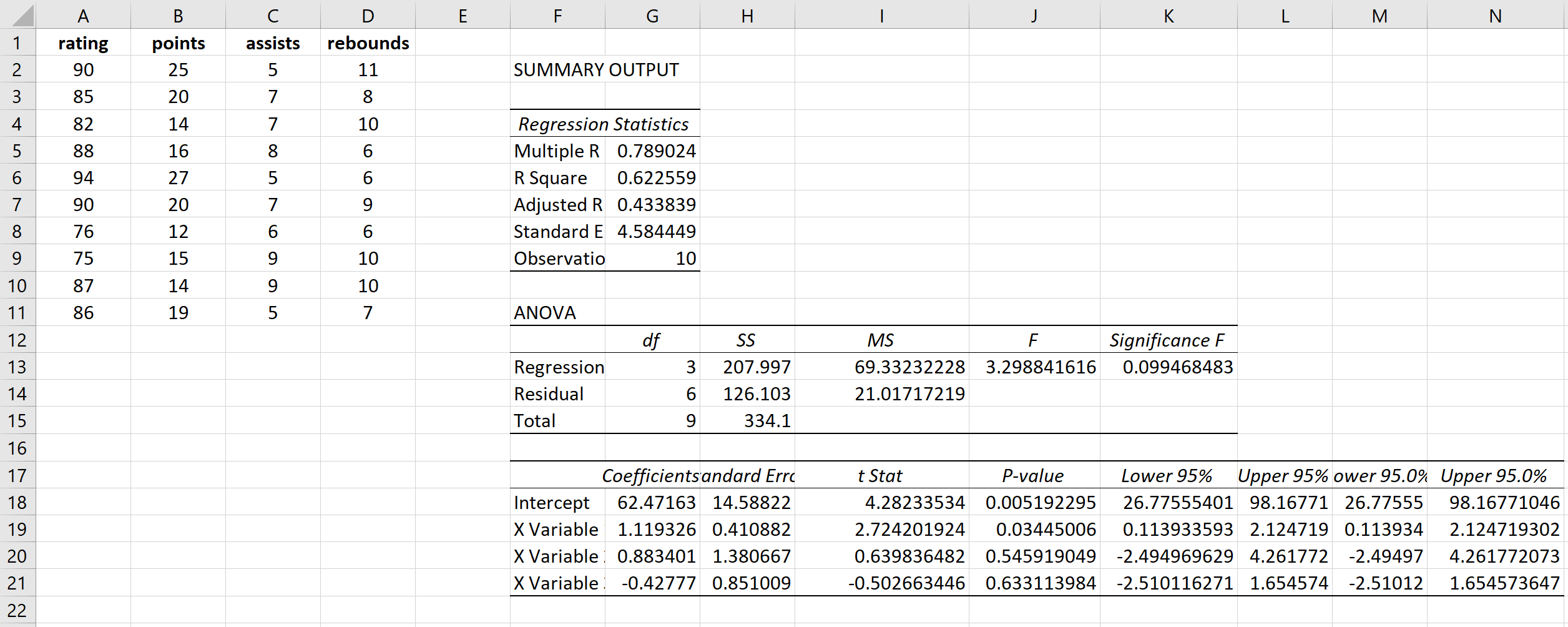
Крок 2: обчисліть квадрати залишків.

Далі ми розрахуємо прогнозовані значення та квадрати залишків для кожного значення відповіді. Для розрахунку прогнозованих значень ми будемо використовувати коефіцієнти з результату регресії:

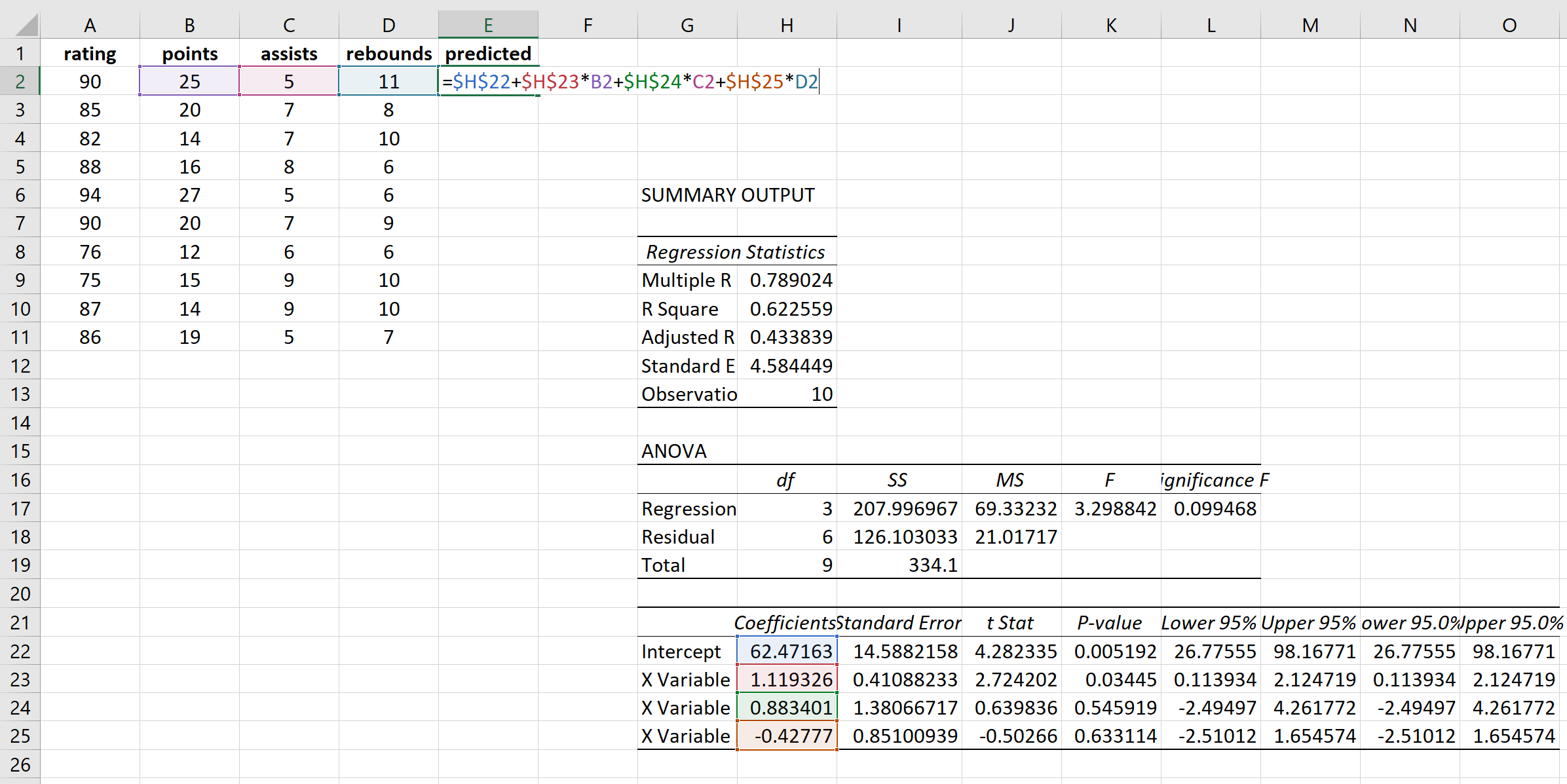
Ми будемо використовувати ту саму формулу, щоб отримати кожне прогнозоване значення:

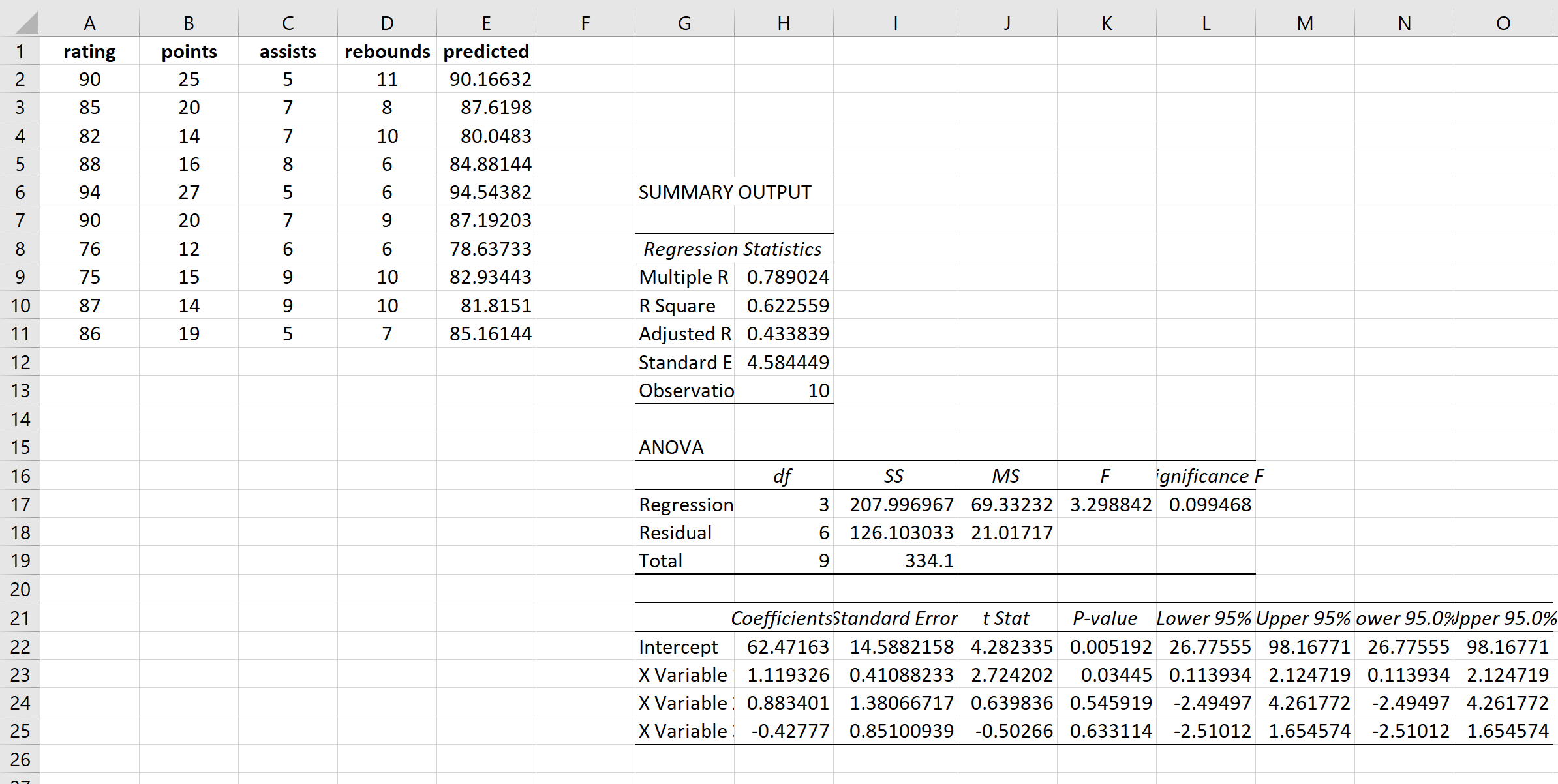
Далі ми обчислимо квадрати залишків для кожного передбачення:

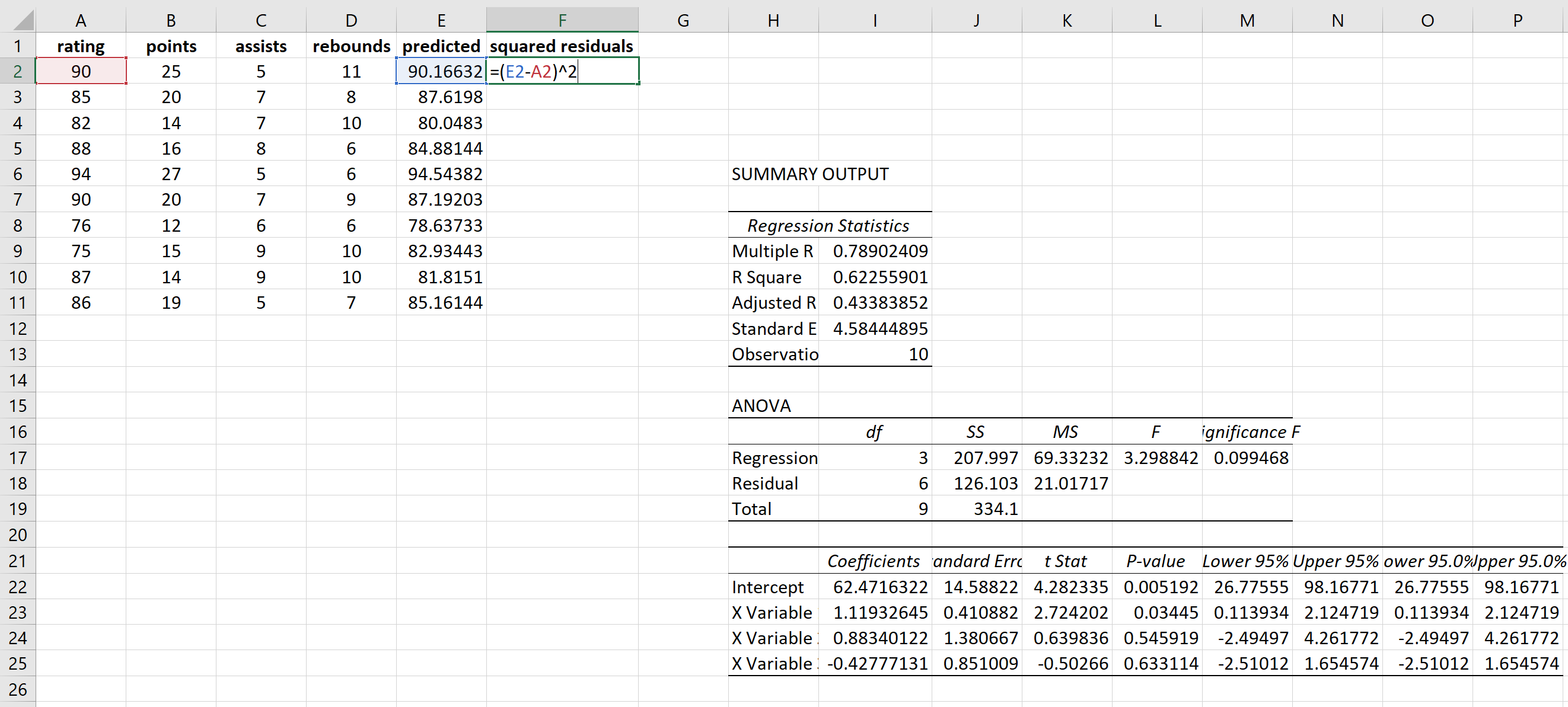
Ми будемо використовувати ту саму формулу для отримання кожного залишкового квадрата:

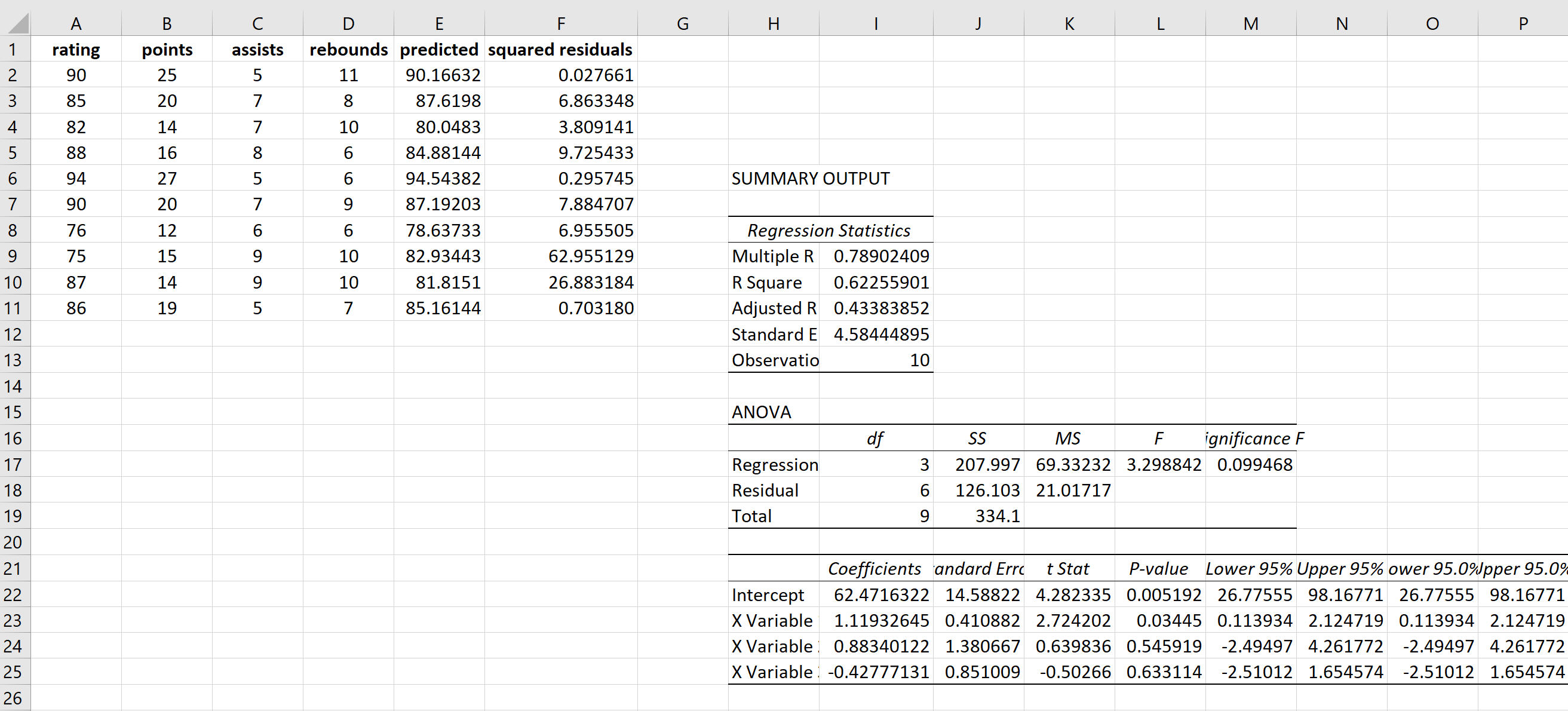
Крок 3: Виконайте нову множинну лінійну регресію, використовуючи квадрати залишків як значення відповіді.

Далі ми виконаємо ті самі кроки, що й раніше, щоб виконати множинну лінійну регресію, використовуючи очки, передачі та підбирання як пояснювальні змінні, за винятком того, що цього разу ми використаємо квадрати залишків як значення відповіді. Ось результат цієї регресії:

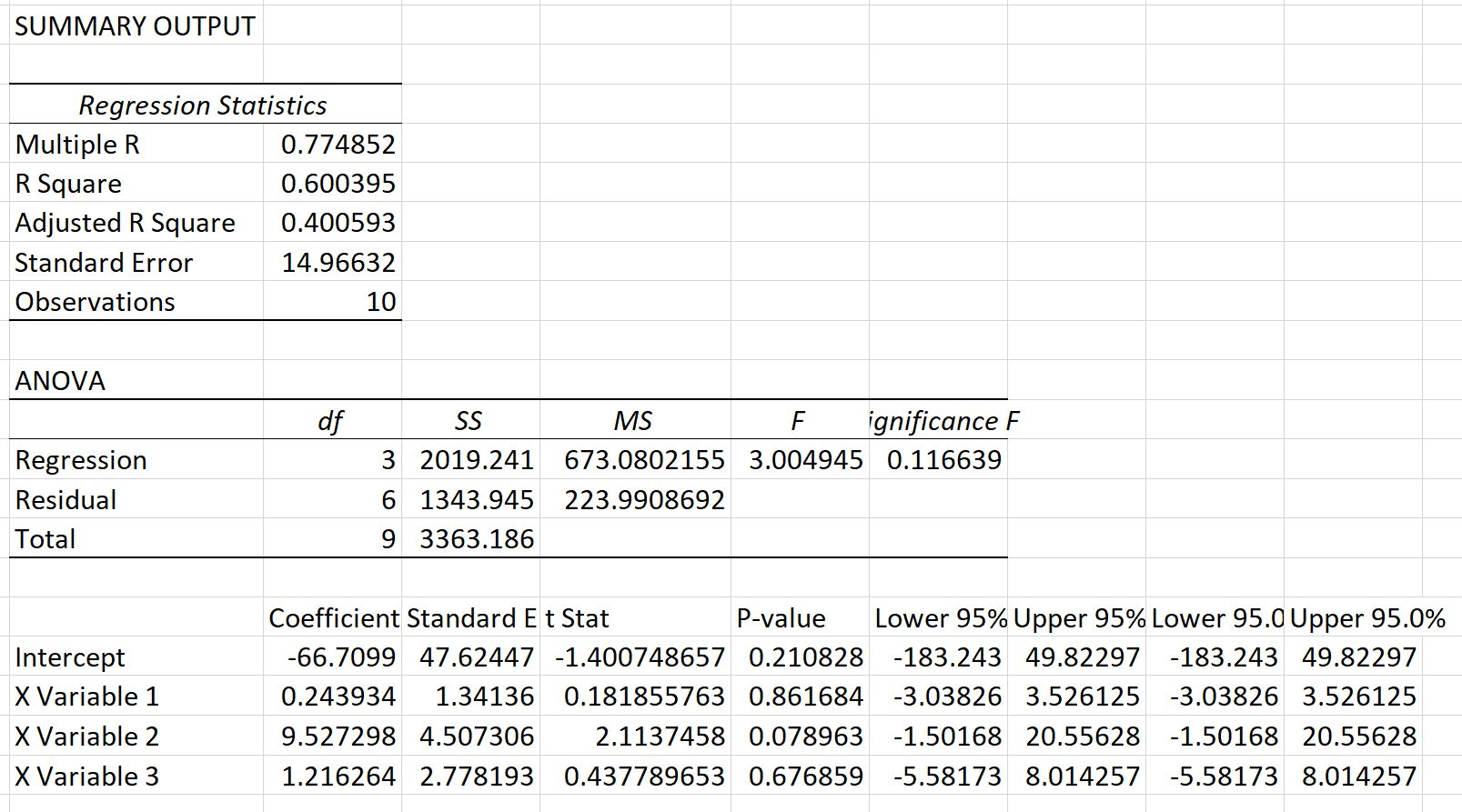
Крок 4: Виконайте тест Брейша-Пейгана.

Нарешті, ми виконаємо тест Брейша-Пейгана, щоб побачити, чи була гетероскедастичність у вихідній регресії.

Спочатку ми розрахуємо статистику хі-квадрат за формулою:

X ² = n*R ² _новий

золото:

n = кількість спостережень

R ² _new = R Квадрат «нової» регресії, в якій квадрати залишків використовувалися як змінна відповіді.

У нашому прикладі ^X2 = 10 * 0,600395 = 6,00395 .

Далі ми знайдемо p-значення, пов’язане з цією тестовою статистикою. Для цього ми можемо використати таку формулу в Excel:

=CHISQ.DIST.RT(тестова статистика, ступені свободи)

У нашому випадку ступені свободи є числом, указаним для регресії df у вихідних даних. У цьому випадку це 3. Отже, наша формула виглядає так:

=CHISQ.DIST.RT(6,00395; 3) = 0,111418 .

Оскільки це p-значення не менше 0,05, ми не можемо відхилити нульову гіпотезу. У нас немає достатніх доказів, щоб стверджувати, що гетероскедастичність присутня в оригінальній моделі регресії.