Як виконати тест брейша-пагана в stata

Множинна лінійна регресія — це метод, який ми можемо використовувати для розуміння зв’язку між декількома пояснювальними змінними та змінною відповіді.

На жаль, проблема, яка часто виникає в регресії, відома як гетероскедастичність , у якій існує систематична зміна дисперсії залишків у діапазоні виміряних значень.

Один тест, який ми можемо використати для визначення наявності гетероскедастичності, це тест Брейша-Пейгана . Цей тест створює статистику хі-квадрат і відповідне значення p.

Якщо p-значення нижче певного порогу (звичайними варіантами є 0,01, 0,05 і 0,10), то є достатньо доказів, щоб стверджувати, що присутня гетероскедастичність.

Цей підручник пояснює, як виконати тест Брейша-Пагана в Stata.

Приклад: тест Брейша-Пагана в Stata

Ми використаємо автоматично інтегрований набір даних Stata, щоб проілюструвати, як виконати тест Брейша-Пейгана.

Крок 1: Завантажте та відобразіть дані.

Спочатку скористайтеся такою командою, щоб завантажити дані:

автоматичне використання системи

Потім відобразіть необроблені дані за допомогою такої команди:

бр

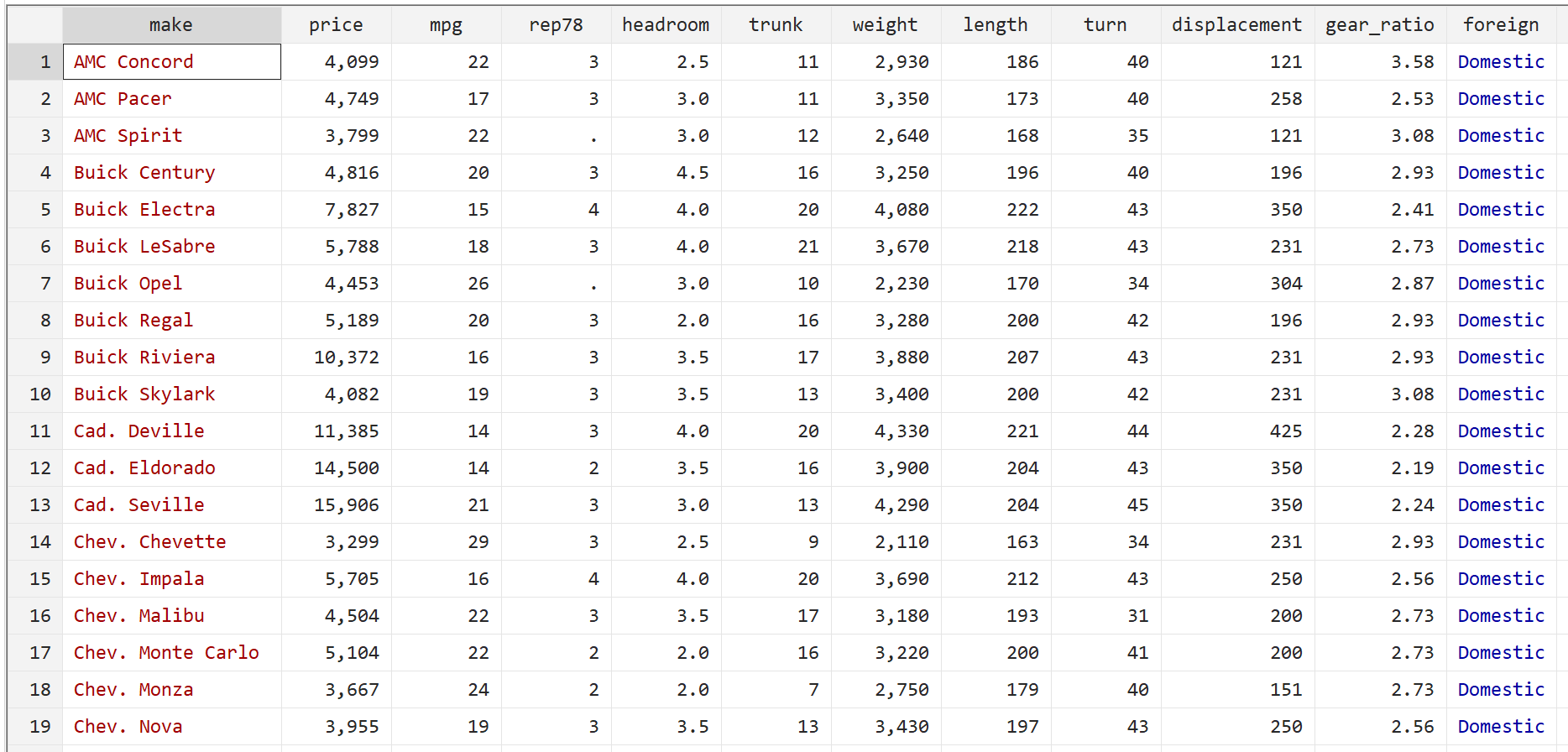
Крок 2: Виконайте множинну лінійну регресію.

Далі ми введемо таку команду, щоб виконати множинну лінійну регресію, використовуючи ціну як змінну відповіді та милі на галон і вагу як пояснювальні змінні:

регресія ціна mpg вага

Крок 3: Виконайте тест Брейша-Пейгана.

Після підгонки регресійної моделі ми можемо виконати тест Брейша-Пагана за допомогою команди hettest , що є скороченням від «тест гетероскедастичності»:

найгарячіший

Ось як інтерпретувати результат:

Хо: це нульова гіпотеза тесту, яка стверджує, що існує постійна дисперсія між залишками.

Змінні: це повідомляє нам про змінну відповіді, яку використовували в регресійній моделі. У цьому випадку це була змінна ціна .

chi2(1): це статистика тесту хі-квадрат. У цьому випадку це 14:78.

Prob > chi2: це p-значення, яке відповідає статистиці тесту хі-квадрат. У цьому випадку це 0,0001. Якщо це значення менше 0,05, ми можемо відхилити нульову гіпотезу та зробити висновок про гетероскедастичність даних.

Що робити далі

Якщо вам не вдалося відхилити нульову гіпотезу тесту Брейша-Пейгана, то гетероскедастичності немає, і ви можете продовжити інтерпретацію результату вихідної регресії.

Однак якщо ви відкидаєте нульову гіпотезу тесту Брейша-Пейгана, це означає, що гетероскедастичність присутня в даних. У цьому випадку стандартні помилки, відображені в таблиці результатів регресії, є ненадійними. Є кілька способів вирішити цю проблему, зокрема:

1. Перетворення змінної відповіді. Ви можете спробувати виконати перетворення змінної відповіді. Наприклад, ви можете використовувати log(price) замість price як змінну відповіді. Загалом, реєстрація змінної відповіді є ефективним способом усунення гетероскедастичності. Іншим поширеним перетворенням є використання квадратного кореня зі змінної відповіді.

2. Використовуйте зважену регресію. Цей тип регресії призначає вагу кожній точці даних на основі дисперсії її підігнаного значення. По суті, це дає низькі ваги точкам даних, які мають більшу дисперсію, зменшуючи їхні залишкові квадрати. Якщо використовуються відповідні ваги, це може усунути проблему гетероскедастичності.

3. Використовуйте надійні стандартні помилки. Надійні стандартні помилки є більш «надійними» до проблеми гетероскедастичності та, як правило, забезпечують більш точне вимірювання справжньої стандартної помилки коефіцієнта регресії. Перегляньте цей підручник , щоб дізнатися, як використовувати надійні стандартні помилки в регресії в Stata.