Як виконати тест брейша-пагана в sas

Критерій Брейша-Пейгана використовується для визначення наявності гетероскедастичності в регресійному аналізі.

Цей підручник пояснює, як виконати тест Брейша-Пагана в SAS.

Приклад: тест Брейша-Пагана в SAS

Припустімо, ми хочемо підібрати модель множинної лінійної регресії, яка використовує кількість годин, витрачених на навчання, і кількість складених практичних іспитів, щоб передбачити оцінку студентів на підсумкових іспитах:

Оцінка за іспит = β ₀ + β ₁ (годин) + β ₂ (підготовчі іспити)

Спочатку ми використаємо наступний код, щоб створити набір даних, що містить цю інформацію для 20 студентів:

 /*create dataset*/
data exam_data;
    input hours prep_exams score;
    datalines ;
1 1 76
2 3 78
2 3 85
4 5 88
2 2 72
1 2 69
5 1 94
4 1 94
2 0 88
4 3 92
4 4 90
3 3 75
6 2 90
5 4 90
3 4 82
4 4 85
6 5 90
2 1 83
1 0 62
2 1 76
;
run ;

/*view dataset*/
proc print data =exam_data; 

Далі ми використаємо модель proc, щоб відповідати цій моделі множинної лінійної регресії, а також твердження Pagan для виконання тесту Брейша-Пейгана на гетероскедастичність:

 /*fit regression model and perform Breusch Pagan test*/
proc model data =exam_data;
    parms a1 b1 b2;
    score = a1 + b1*hours + b2*prep_exams;
    fit score / pagan=(1 hours prep_exams)
    out =resid1 outsid ;
run ;
quit ; 

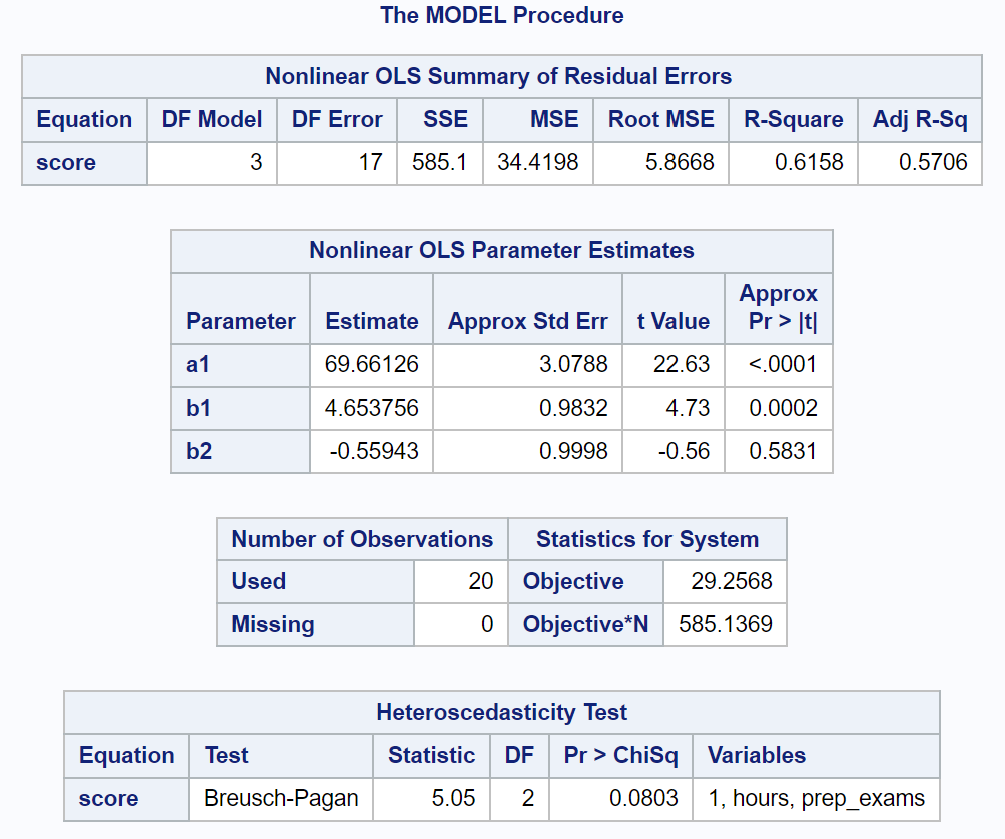
Остання таблиця результатів показує результати тесту Брейша-Пагана.

З цієї таблиці ми бачимо, що статистика тесту становить 5,05 , а відповідне значення p — 0,0803 .

Оскільки p-значення не менше 0,05, ми не можемо відхилити нульову гіпотезу.

Це означає, що ми не маємо достатніх доказів, щоб стверджувати, що гетероскедастичність присутня в регресійній моделі.

Тому можна безпечно інтерпретувати стандартні помилки оцінок коефіцієнтів у підсумковій таблиці регресії.

Що робити далі

Якщо вам не вдалося відхилити нульову гіпотезу тесту Брейша-Пейгана, то гетероскедастичність відсутня, і ви можете продовжити інтерпретацію результату вихідної регресії.

Однак якщо ви відкидаєте нульову гіпотезу, це означає, що гетероскедастичність присутня в даних. У цьому випадку стандартні помилки, відображені в таблиці результатів регресії, можуть бути ненадійними.

Існує кілька поширених способів вирішення цієї проблеми, зокрема:

1. Перетворення змінної відповіді. Ви можете спробувати виконати перетворення змінної відповіді.

Наприклад, ви можете використовувати змінну відповіді журналу замість початкової змінної відповіді.

Загалом реєстрування змінної відповіді є ефективним способом усунення гетероскедастичності.

Іншим поширеним перетворенням є використання квадратного кореня зі змінної відповіді.

2. Використовуйте зважену регресію. Цей тип регресії призначає вагу кожній точці даних на основі дисперсії її підігнаного значення.

Це дає невеликі ваги точкам даних, які мають більшу дисперсію, зменшуючи їхні залишкові квадрати.

Якщо використовуються відповідні ваги, це може усунути проблему гетероскедастичності.