Як використовувати звичайний cdf у r (з прикладами)
Для роботи зі звичайною CDF (інтегральною функцією розподілу) у R можна використовувати наступні методи:
Спосіб 1: Розрахунок нормальної вірогідності CDF
#calculate probability that random value is less than 1.96 in normal CDF pnorm(1.96) #calculate probability that random value is greater than 1.96 in normal CDF pnorm(1.96, lower.tail = FALSE )
Спосіб 2. Побудуйте графік нормальної CDF
#define sequence of x-values x <- seq(-4, 4, .01) #calculate normal CDF probabilities prob <- pnorm(x) #normal plot CDF plot(x, prob, type=" l ")
Наступні приклади показують, як використовувати ці методи на практиці.
Приклад 1: Розрахувати нормальні ймовірності CDF
У наступному коді показано, як обчислити ймовірність того, що випадкова змінна приймає значення менше 1,96 у стандартному нормальному розподілі:
#calculate probability that random value is less than 1.96 in normal CDF
pnorm(1.96)
[1] 0.9750021
Імовірність того, що випадкова змінна приймає значення менше 1,96 у стандартному нормальному розподілі, дорівнює 0,975 .
Ми також можемо знайти ймовірність того, що випадкова змінна приймає значення більше 1,96 за допомогою аргументу lower.tail :
#calculate probability that random value is greater than 1.96 in normal CDF pnorm(1.96, lower.tail = FALSE ) [1] 0.0249979
І ми можемо використовувати такий синтаксис, щоб знайти ймовірність того, що випадкова змінна приймає значення між двома значеннями в стандартному нормальному розподілі:
#calculate probability that random value takes on value between -1.96 and 1.96
pnorm(1.96) - pnorm(-1.96)
[1] 0.9500042
Імовірність того, що випадкова змінна приймає значення від -1,96 до 1,96 у стандартному нормальному розподілі, дорівнює 0,95 .
Приклад 2: Побудова нормальної CDF
У наступному коді показано, як побудувати звичайну CDF:
#define sequence of x-values x <- seq(-4, 4, .01) #calculate normal CDF probabilities prob <- pnorm(x) #normal plot CDF plot(x, prob, type=" l ")
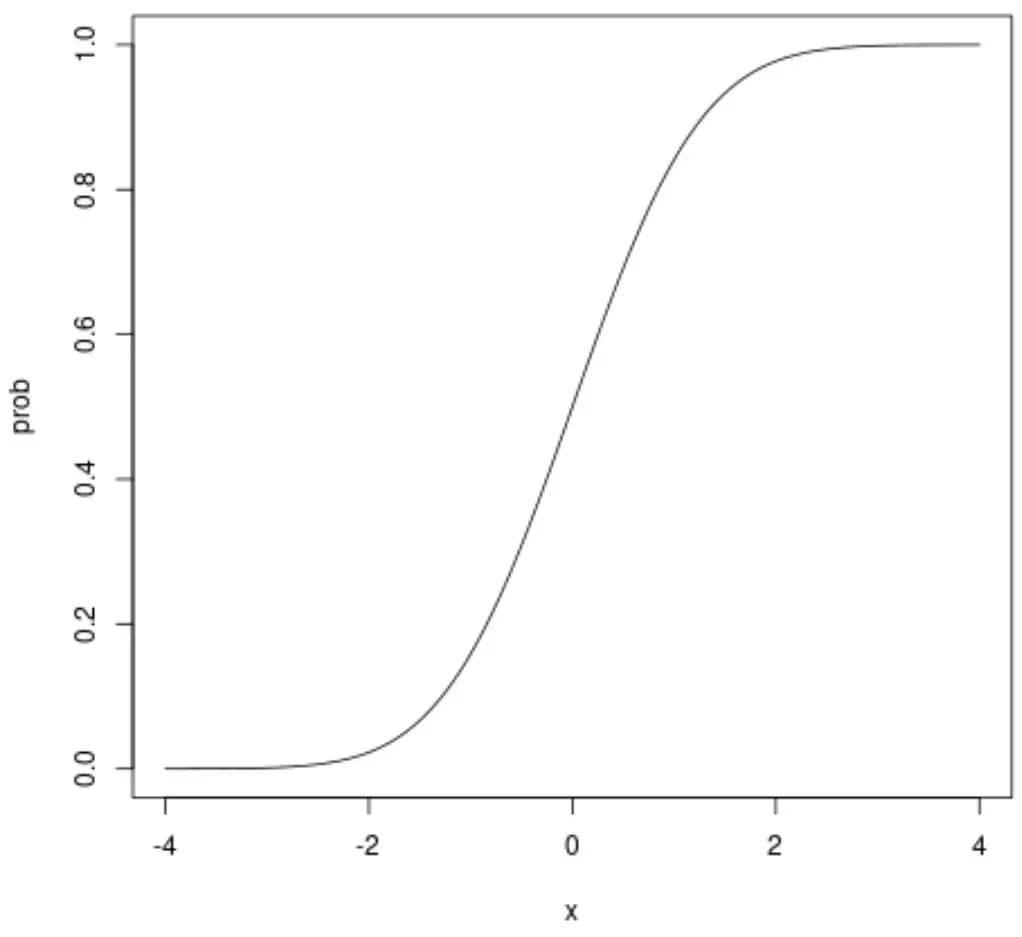
На осі абсцис відображаються значення випадкової величини, яка відповідає стандартному нормальному розподілу, а на осі у – ймовірність того, що випадкова змінна приймає значення, менше значення, показаного на осі абсцис.
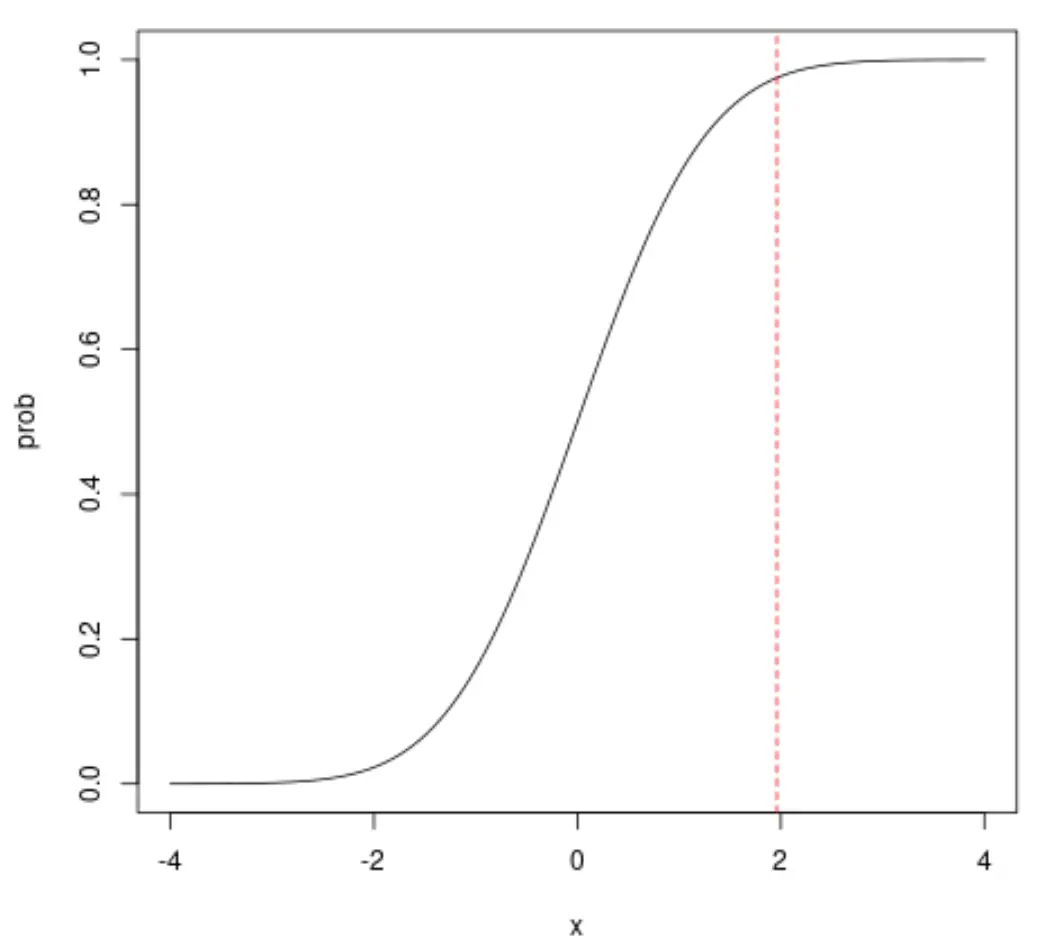
Наприклад, якщо ми подивимося на x = 1,96, ми побачимо, що кумулятивна ймовірність того, що x менше 1,96, дорівнює приблизно 0,975:
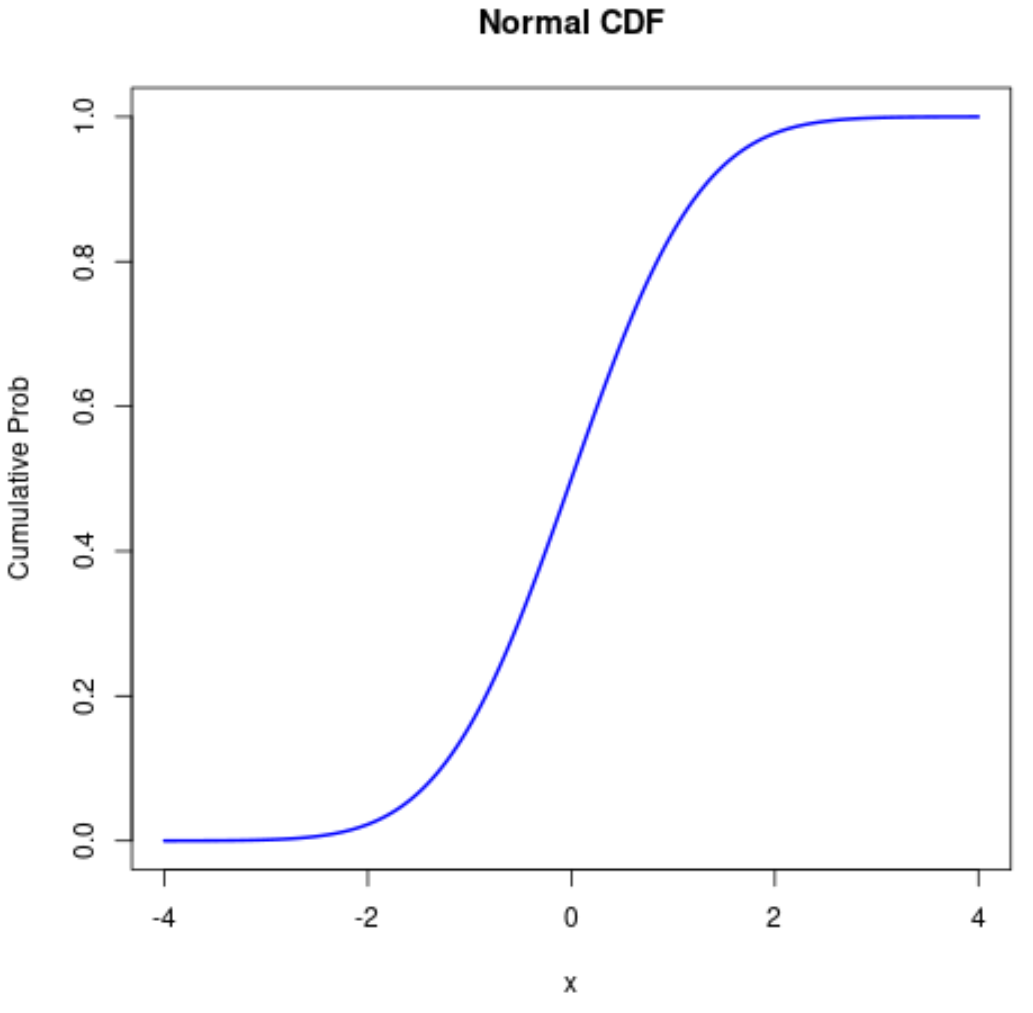
Зауважте, що ви також можете змінити естетику звичайного сюжету CDF:
#define sequence of x-values x <- seq(-4, 4, .01) #calculate normal CDF probabilities prob <- pnorm(x) #normal plot CDF plot(x, prob, type=' l ', col=' blue ', lwd= 2 , main=' Normal CDF ', ylab=' Cumulative Prob ')
Пов’язане: як використовувати функцію seq у R
Додаткові ресурси
У наступних посібниках пояснюється, як виконувати інші типові операції в R:
Як побудувати графік нормального розподілу в R
Як розрахувати Z бали в R
Посібник із dnorm, pnorm, qnorm і rnorm у R