Як розрахувати dfbetas у r

У статистиці ми часто хочемо знати, який вплив мають різні спостереження на регресійні моделі.

Один із способів обчислення впливу спостережень – це використання метрики, відомої як DFBETAS , яка повідомляє нам про стандартизований вплив на кожен коефіцієнт вилучення кожного окремого спостереження.

Ця метрика дає нам уявлення про вплив кожного спостереження на кожну оцінку коефіцієнта в заданій моделі регресії.

Цей підручник демонструє покроковий приклад того, як обчислити та візуалізувати DFBETAS для кожного спостереження в моделі в R.

Крок 1: Створіть регресійну модель

Спочатку ми створимо модель множинної лінійної регресії, використовуючи набір даних mtcars , вбудований у R:

 #fit a regression model
model <- lm(mpg~disp+hp, data=mtcars)

#view model summary
summary(model)

Coefficients:
             Estimate Std. Error t value Pr(>|t|)    
(Intercept) 30.735904 1.331566 23.083 < 2nd-16 ***
available -0.030346 0.007405 -4.098 0.000306 ***
hp -0.024840 0.013385 -1.856 0.073679 .  
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 3.127 on 29 degrees of freedom
Multiple R-squared: 0.7482, Adjusted R-squared: 0.7309 
F-statistic: 43.09 on 2 and 29 DF, p-value: 2.062e-09

Крок 2: Обчисліть DFBETAS для кожного спостереження

Далі ми використаємо вбудовану функцію dfbetas() , щоб обчислити значення DFBETAS для кожного спостереження в моделі:

 #calculate DFBETAS for each observation in the model
dfbetas <- as . data . frame (dfbetas(model))

#display DFBETAS for each observation
dfbetas

                      (Intercept) disp hp
Mazda RX4 -0.1174171253 0.030760632 1.748143e-02
Mazda RX4 Wag -0.1174171253 0.030760632 1.748143e-02
Datsun 710 -0.1694989349 0.086630144 -3.332781e-05
Hornet 4 Drive 0.0577309674 0.078971334 -8.705488e-02
Hornet Sportabout -0.0204333878 0.237526523 -1.366155e-01
Valiant -0.1711908285 -0.139135639 1.829038e-01
Duster 360 -0.0312338677 -0.005356209 3.581378e-02
Merc 240D -0.0312259577 -0.010409922 2.433256e-02
Merc 230 -0.0865872595 0.016428917 2.287867e-02
Merc 280 -0.1560683502 0.078667906 -1.911180e-02
Merc 280C -0.2254489597 0.113639937 -2.760800e-02
Merc 450SE 0.0022844093 0.002966155 -2.855985e-02
Merc 450SL 0.0009062022 0.001176644 -1.132941e-02
Merc 450SLC 0.0041566755 0.005397169 -5.196706e-02
Cadillac Fleetwood 0.0388832216 -0.134511133 7.277283e-02
Lincoln Continental 0.0483781688 -0.121146607 5.326220e-02
Chrysler Imperial -0.1645266331 0.236634429 -3.917771e-02
Fiat 128 0.5720358325 -0.181104179 -1.265475e-01
Honda Civic 0.3490872162 -0.053660545 -1.326422e-01
Toyota Corolla 0.7367058819 -0.268512348 -1.342384e-01
Toyota Corona -0.2181110386 0.101336902 5.945352e-03
Dodge Challenger -0.0270169005 -0.123610713 9.441241e-02
AMC Javelin -0.0406785103 -0.141711468 1.074514e-01
Camaro Z28 0.0390139262 0.012846225 -5.031588e-02
Pontiac Firebird -0.0549059340 0.574544346 -3.689584e-01
Fiat X1-9 0.0565157245 -0.017751582 -1.262221e-02
Porsche 914-2 0.0839169111 -0.028670987 -1.240452e-02
Lotus Europa 0.3444562478 -0.402678927 2.135224e-01
Ford Pantera L -0.1598854695 -0.094184733 2.320845e-01
Ferrari Dino -0.0343997122 0.248642444 -2.344154e-01
Maserati Bora -0.3436265545 -0.511285637 7.319066e-01
Volvo 142E -0.1784974091 0.132692956 -4.433915e-02

Для кожного спостереження ми можемо побачити різницю в оцінці коефіцієнта для джерела, змінної disp і змінної hp , яка виникає, коли ми видаляємо це конкретне спостереження.

Загалом ми вважаємо, що спостереження має сильний вплив на оцінку заданого коефіцієнта, якщо воно має значення DBETAS більше за порогове значення 2/√ n , де n – кількість спостережень.

У цьому прикладі порогове значення буде 0,3535534 :

 #find number of observations
n <- nrow (mtcars)

#calculate DFBETAS threshold value
thresh <- 2/ sqrt (n)

thresh

[1] 0.3535534

Крок 3: Візуалізуйте DFBETAS

Нарешті, ми можемо створити графіки для візуалізації значення DFBETAS для кожного спостереження та для кожного предиктора в моделі:

 #specify 2 rows and 1 column in plotting region
by(mfrow=c(2,1))

#plot DFBETAS for disp with threshold lines
plot(dfbetas$disp, type=' h ')
abline(h = thresh, lty = 2)
abline(h = -thresh, lty = 2)

#plot DFBETAS for hp with threshold lines 
plot(dfbetas$hp, type=' h ')
abline(h = thresh, lty = 2)
abline(h = -thresh, lty = 2)

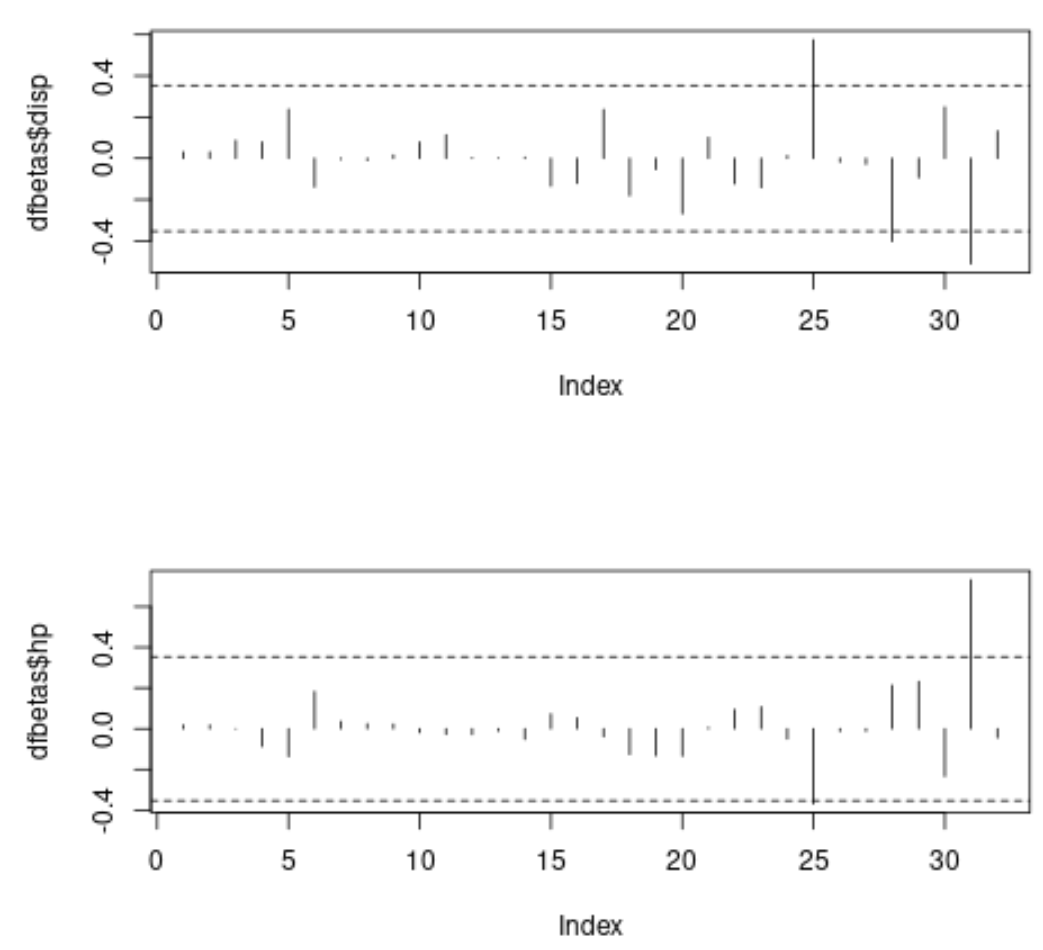
На кожному графіку вісь x відображає індекс кожного спостереження в наборі даних, а значення y відображає відповідний DFBETAS для кожного спостереження та кожного предиктора.

На першому графіку ми бачимо, що три спостереження перевищують абсолютне порогове значення 0,3535534 , а на другому графіку ми бачимо, що два спостереження перевищують абсолютне порогове значення.

Ми можемо вирішити уважніше вивчити ці спостереження, щоб визначити, чи мають вони надмірний вплив на оцінку коефіцієнтів моделі.

Додаткові ресурси

Як виконати просту лінійну регресію в R
Як виконати множинну лінійну регресію в R
Як розрахувати статистику кредитного плеча в R
Як розрахувати DFFITS у R