Excel: як інтерпретувати вихідні дані функції лінійний

Ви можете використовувати функцію LINEST , щоб підібрати модель регресії в Excel.

Ця функція використовує такий базовий синтаксис:

 LINEST(known_y's, known_x's, const, stats)

золото:

• відомі_y : стовпець значень для змінної відповіді
• відомі_x : один або кілька стовпців значень для змінних предиктора
• const : TRUE = нормально обчислити перехоплення, FALSE = примусове перехоплення до нуля
• stats : TRUE = розрахувати додаткову статистику регресії, FALSE = обчислити лише коефіцієнти

У наступному прикладі показано, як інтерпретувати вихідні дані функції ЛІНІЙ на практиці.

Приклад: як інтерпретувати вихід LINEST в Excel

Припустімо, що ми маємо наступний набір даних, який містить змінну предиктора (x) і змінну відповіді (y):

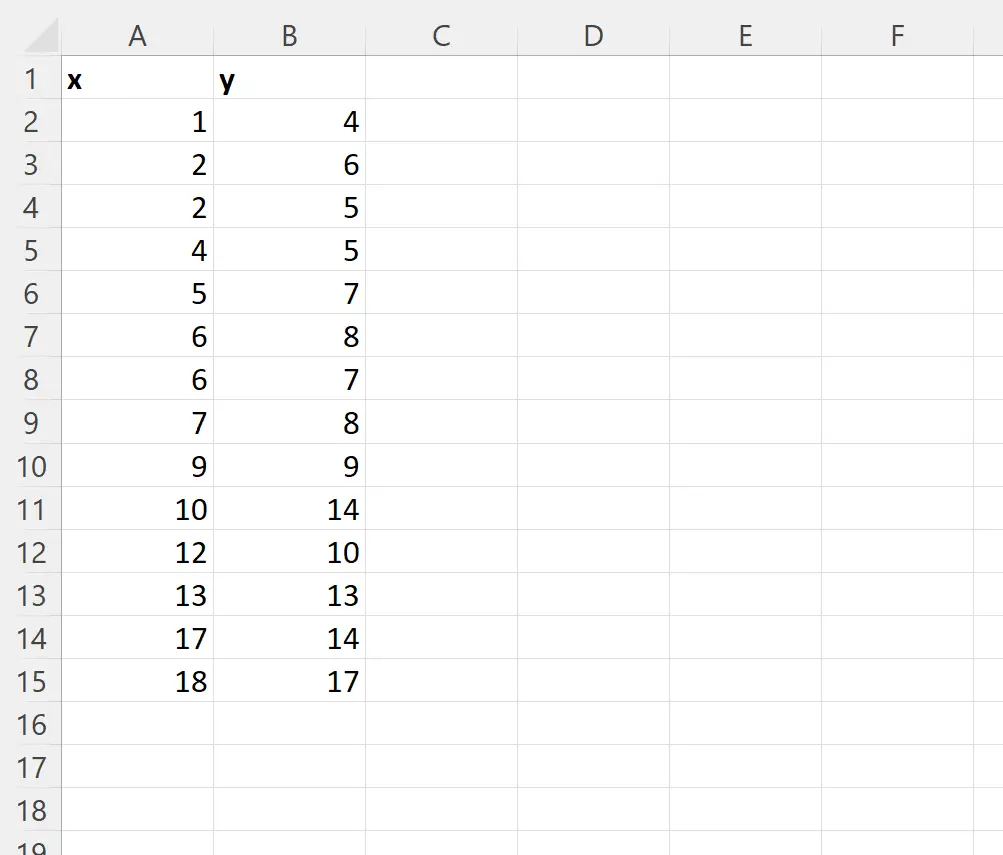
Ми можемо ввести таку формулу в клітинку D1 , щоб виконати просту лінійну регресію з цим набором даних:

 =LINEST( A2:A15 , B2:B15 , TRUE, TRUE)

Вихідні дані функції ЛІНІЙНИЙ містять коефіцієнти моделі регресії, а також кілька додаткових статистичних даних:

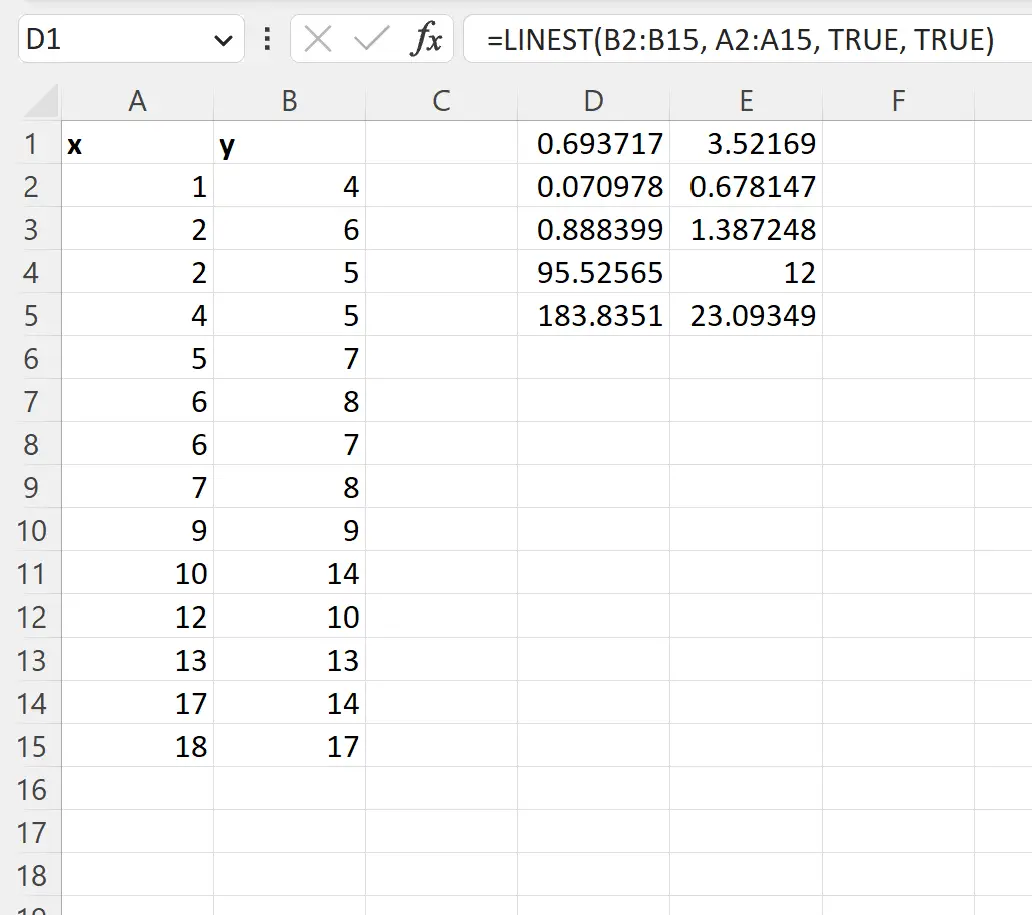
На наступному знімку екрана наведено пояснення кожного значення в результаті:

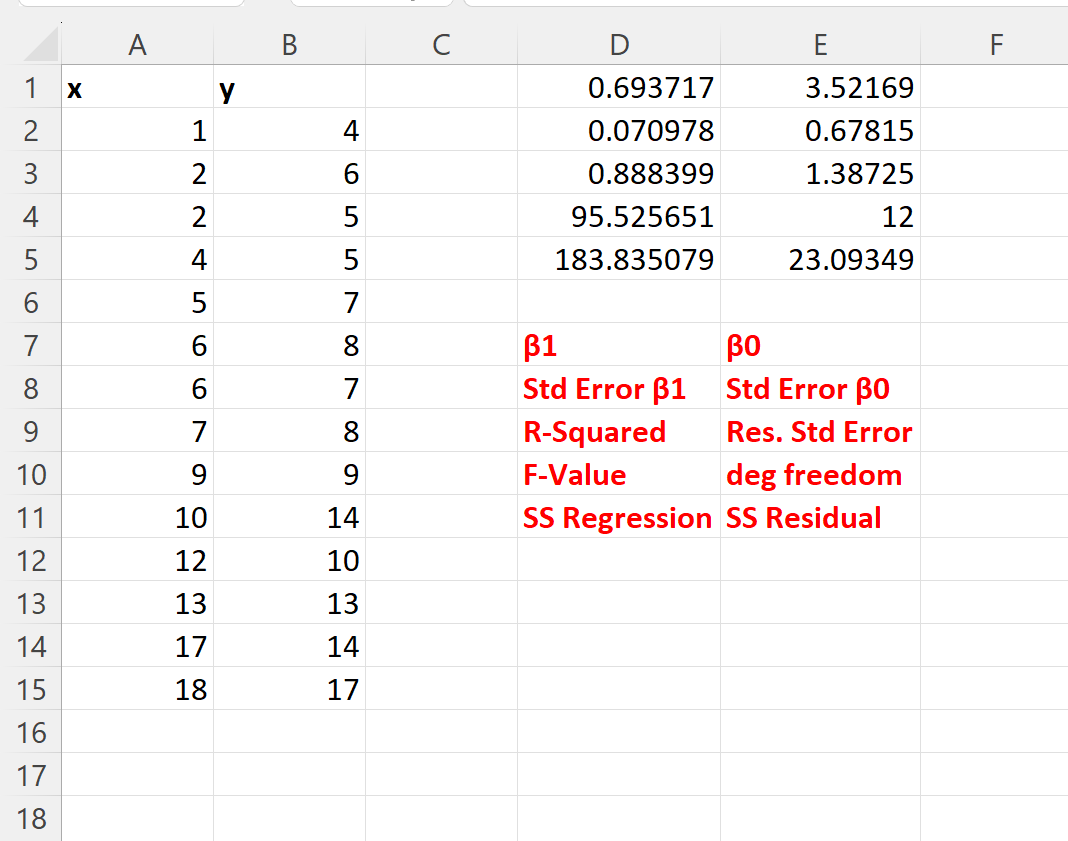
З результату ми бачимо:

• Коефіцієнт для β ₀ становить 3,52169 .
• Коефіцієнт для _β1 становить 0,693717 .

Використовуючи ці значення, ми можемо написати рівняння для цієї простої моделі регресії:

y = 3,52169 + 0,693717(x)

Ми інтерпретуємо це так, що кожне додаткове збільшення на одну одиницю змінної предиктора x пов’язане із середнім збільшенням змінної відповіді y на 0,693717 .

Ми інтерпретуємо вихідний термін так, що коли x дорівнює нулю, середнє значення y дорівнює 3,52169 .

Ми також можемо побачити:

• Значення R-квадрат моделі становить 0,888 .

Ми інтерпретуємо це так, що змінна предиктора здатна пояснити 88,8% варіації змінної відповіді моделі.

За темою: що таке хороше значення R-квадрат?

Додаткові ресурси

У наступних посібниках надається додаткова інформація про регресію в Excel:

Як інтерпретувати значення P у виводі регресії в Excel
Як додати лінію регресії до діаграми розсіювання в Excel
Як виконати поліноміальну регресію в Excel