Як використовувати invnorm на калькуляторі ti-84 (з прикладами)
Ви можете використовувати функцію invNorm() на калькуляторі TI-84, щоб знайти критичні значення z, пов’язані з нормальним розподілом .
Ця функція використовує такий синтаксис:
invNorm(імовірність, μ, σ)
золото:
- ймовірність: рівень значущості
- μ: середня популяція
- σ: стандартне відхилення сукупності
Ви можете отримати доступ до цієї функції на калькуляторі TI-84, натиснувши 2nd, а потім натиснувши VARS . Це приведе вас до екрана DISTR , де ви зможете використовувати invNorm() :

Наступні приклади показують, як використовувати цю функцію на практиці.
Приклад 1: Критичне значення Z для одностороннього тестування
Припустимо, дослідник проводить перевірку гіпотези лівою рукою, використовуючи α = 0,05. Яке z-критичне значення відповідає цьому альфа-рівню?
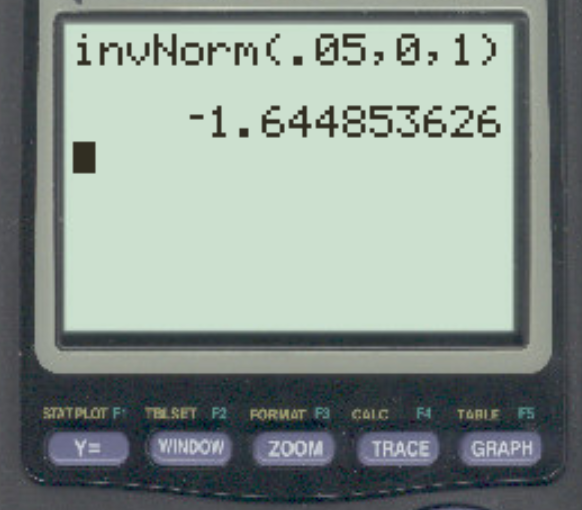
Відповідь: z = -1,64485 .
Припустимо, дослідник проводить пряму перевірку гіпотези, використовуючи α = 0,05. Яке z-критичне значення відповідає цьому альфа-рівню?
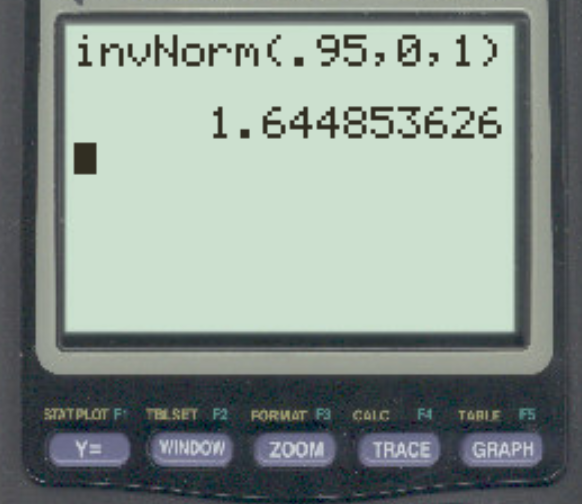
Відповідь: z = 1,64485 .
Приклад 2: Критичне значення Z для двосторонніх тестів
Припустимо, що дослідник проводить двобічний тест гіпотези, використовуючи α = 0,05. Яке z-критичне значення відповідає цьому альфа-рівню?
Щоб знайти це критичне значення, можна скористатися формулою 1 – α/2. У цьому випадку ми будемо використовувати 1 – 0,05/2 = 0,975 для ймовірності:
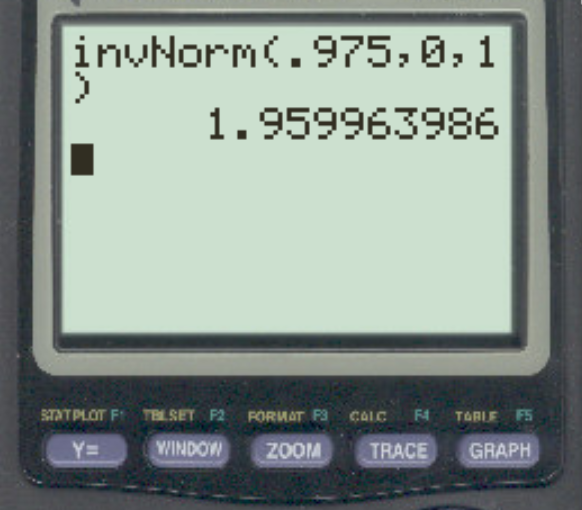
Відповідь: z = 1,96 .
Приклад 3: Критичне значення Z для граничних показників
Припустімо, що бали за конкретний іспит зазвичай розподіляються із середнім значенням 70 і стандартним відхиленням 8. Який бал відокремлює 10% найкращих від решти?
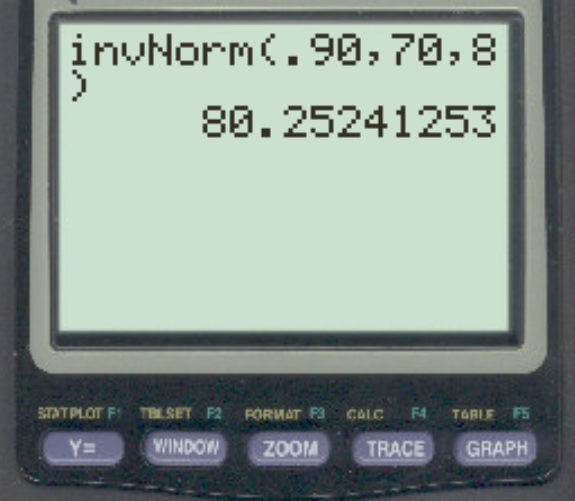
Відповідь: 80,25 .
Припустімо, що зріст чоловіків у певному місті зазвичай розподіляється із середнім значенням 68 дюймів і стандартним відхиленням 4 дюйми. Яка висота відокремлює нижні 25% від решти?
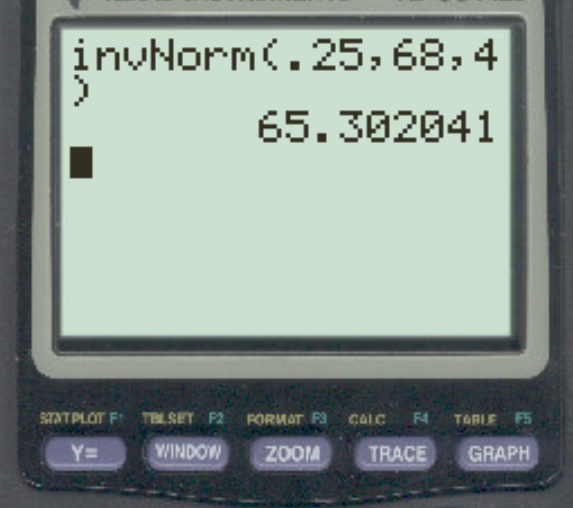
Відповідь: 65,3 дюйма.
Додаткові ресурси
Як обчислити біноміальні ймовірності на калькуляторі TI-84
Як розрахувати ймовірності Пуассона на калькуляторі TI-84
Як обчислити геометричні ймовірності на калькуляторі TI-84