Кластеризація k-середніх у r: покроковий приклад

Кластеризація – це техніка машинного навчання, яка намагається знайти групи спостережень у наборі даних.

Мета полягає в тому, щоб знайти такі кластери, щоб спостереження всередині кожного кластера були досить подібними одне до одного, тоді як спостереження в різних кластерах сильно відрізнялися одне від одного.

Кластеризація є формою неконтрольованого навчання , оскільки ми просто намагаємося знайти структуру в наборі даних, а не передбачити значення змінної відповіді .

Кластеризація часто використовується в маркетингу, коли компанії мають доступ до такої інформації, як:

• Доходи домашніх господарств
• Розмір домогосподарства
• Голова домашнього господарства Професія
• Відстань до найближчого населеного пункту

Коли ця інформація доступна, кластеризацію можна використати для виявлення домогосподарств, які схожі та з більшою ймовірністю купуватимуть певні продукти або краще реагуватимуть на певний тип реклами.

Одна з найпоширеніших форм кластеризації відома як k-середнє кластеризування .

Що таке K-Means Clustering?

Кластеризація K-означає – це техніка, за якої ми поміщаємо кожне спостереження з набору даних в один із K кластерів.

Кінцева мета полягає в тому, щоб мати K кластерів, у яких спостереження всередині кожного кластера досить подібні одне до одного, тоді як спостереження в різних кластерах досить відрізняються одне від одного.

На практиці ми використовуємо такі кроки для кластеризації K-середніх:

1. Виберіть значення для K.

• По-перше, нам потрібно вирішити, скільки кластерів ми хочемо визначити в даних. Часто нам просто потрібно перевірити кілька різних значень K і проаналізувати результати, щоб побачити, яка кількість кластерів є найбільш доцільною для даної проблеми.

2. Випадково призначте кожне спостереження початковому кластеру від 1 до K.

3. Виконуйте наступну процедуру, доки призначення кластера не перестануть змінюватися.

• Для кожного з K кластерів обчисліть центр тяжіння кластера. Це просто вектор p- середніх ознак для спостережень k-го кластера.
• Призначте кожне спостереження кластеру з найближчим центроїдом. Тут найближче визначається за допомогою евклідової відстані .

Кластеризація K-середніх у R

У наступному посібнику наведено покроковий приклад того, як виконати кластеризацію k-середніх у R.

Крок 1: Завантажте необхідні пакети

Спочатку ми завантажимо два пакети, що містять кілька корисних функцій для кластеризації k-середніх у R.

 library (factoextra)
library (cluster)

Крок 2: Завантажте та підготуйте дані

Для цього прикладу ми використаємо набір даних USArrests , вбудований у R, який містить кількість арештів на 100 000 осіб у кожному штаті США у 1973 році за вбивства , напади та зґвалтування , а також відсоток населення кожного штату, що живе в містах. області. , UrbanPop .

Наступний код показує, як зробити наступне:

• Завантажити набір даних USArrests
• Видаліть усі рядки з відсутніми значеннями
• Масштабуйте кожну змінну в наборі даних, щоб мати середнє значення 0 і стандартне відхилення 1

 #load data
df <-USArrests

#remove rows with missing values
df <- na. omitted (df)

#scale each variable to have a mean of 0 and sd of 1
df <- scale(df)

#view first six rows of dataset
head(df)

               Murder Assault UrbanPop Rape
Alabama 1.24256408 0.7828393 -0.5209066 -0.003416473
Alaska 0.50786248 1.1068225 -1.2117642 2.484202941
Arizona 0.07163341 1.4788032 0.9989801 1.042878388
Arkansas 0.23234938 0.2308680 -1.0735927 -0.184916602
California 0.27826823 1.2628144 1.7589234 2.067820292
Colorado 0.02571456 0.3988593 0.8608085 1.864967207

Крок 3: Знайдіть оптимальну кількість кластерів

Щоб виконати кластеризацію k-середніх у R, ми можемо використати вбудовану функцію kmeans() , яка використовує такий синтаксис:

kmeans (дані, центри, nstart)

золото:

• дані: назва набору даних.
• центри: кількість кластерів, позначена k .
• nstart: кількість початкових конфігурацій. Оскільки можливо, що різні початкові початкові кластери призведуть до різних результатів, рекомендується використовувати кілька різних початкових конфігурацій. Алгоритм k-середніх знайде початкові конфігурації, які призведуть до найменшої варіації в кластері.

Оскільки ми не знаємо заздалегідь, скільки кластерів є оптимальним, ми створимо два різних графіки, які допоможуть нам вирішити:

1. Кількість кластерів відносно загальної суми квадратів

Спочатку ми використаємо функцію fviz_nbclust() , щоб побудувати графік залежності кількості кластерів від загальної суми квадратів:

 fviz_nbclust(df, kmeans, method = “ wss ”) 

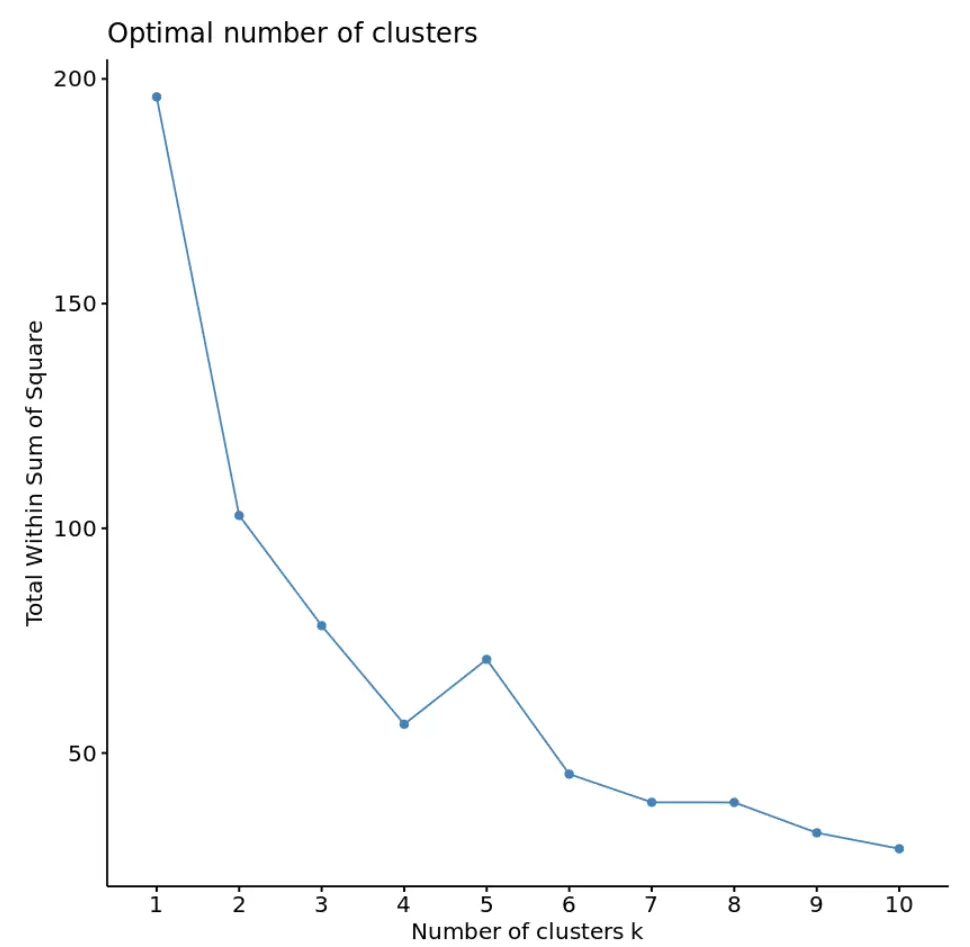
Як правило, коли ми створюємо такий тип графіка, ми шукаємо «коліно», де сума квадратів починає «згинатися» або вирівнюватися. Загалом це оптимальна кількість кластерів.

Для цього графіка здається, що є невеликий перегин або «вигин» при k = 4 кластерах.

2. Кількість кластерів у порівнянні зі статистикою прогалин

Іншим способом визначення оптимальної кількості кластерів є використання метрики під назвою статистика відхилення , яка порівнює загальну внутрішньокластерну варіацію для різних значень k з їх очікуваними значеннями для розподілу без кластеризації.

Ми можемо обчислити статистику розриву для кожної кількості кластерів за допомогою функції clusGap() із пакета кластерів , а також побудувати графік кластерів зі статистикою розриву за допомогою функції fviz_gap_stat() :

 #calculate gap statistic based on number of clusters
gap_stat <- clusGap(df,
                    FUN = kmeans,
                    nstart = 25,
                    K.max = 10,
                    B = 50)

#plot number of clusters vs. gap statistic
fviz_gap_stat(gap_stat) 

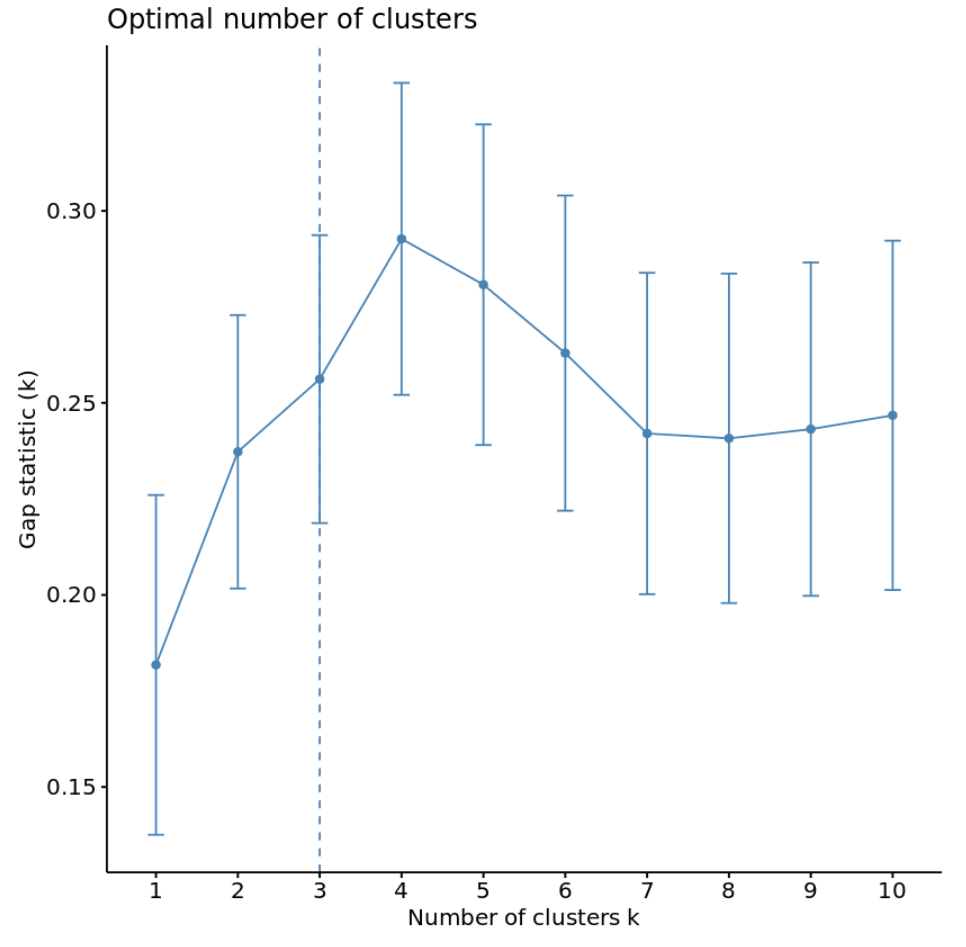
З графіка ми можемо побачити, що статистика розриву найвища при k = 4 кластерах, що відповідає методу ліктя, який ми використовували раніше.

Крок 4: Виконайте кластеризацію K-Means з оптимальним K

Нарешті, ми можемо виконати кластеризацію k-середніх на наборі даних, використовуючи оптимальне значення для k , рівне 4:

 #make this example reproducible
set.seed(1)

#perform k-means clustering with k = 4 clusters
km <- kmeans(df, centers = 4, nstart = 25)

#view results
km

K-means clustering with 4 clusters of sizes 16, 13, 13, 8

Cluster means:
      Murder Assault UrbanPop Rape
1 -0.4894375 -0.3826001 0.5758298 -0.26165379
2 -0.9615407 -1.1066010 -0.9301069 -0.96676331
3 0.6950701 1.0394414 0.7226370 1.27693964
4 1.4118898 0.8743346 -0.8145211 0.01927104

Vector clustering:
       Alabama Alaska Arizona Arkansas California Colorado 
             4 3 3 4 3 3 
   Connecticut Delaware Florida Georgia Hawaii Idaho 
             1 1 3 4 1 2 
      Illinois Indiana Iowa Kansas Kentucky Louisiana 
             3 1 2 1 2 4 
         Maine Maryland Massachusetts Michigan Minnesota Mississippi 
             2 3 1 3 2 4 
      Missouri Montana Nebraska Nevada New Hampshire New Jersey 
             3 2 2 3 2 1 
    New Mexico New York North Carolina North Dakota Ohio Oklahoma 
             3 3 4 2 1 1 
        Oregon Pennsylvania Rhode Island South Carolina South Dakota Tennessee 
             1 1 1 4 2 4 
         Texas Utah Vermont Virginia Washington West Virginia 
             3 1 2 1 1 2 
     Wisconsin Wyoming 
             2 1 

Within cluster sum of squares by cluster:
[1] 16.212213 11.952463 19.922437 8.316061
 (between_SS / total_SS = 71.2%)

Available components:

[1] "cluster" "centers" "totss" "withinss" "tot.withinss" "betweenss"   
[7] "size" "iter" "ifault"         

З результатів ми бачимо, що:

• До першого кластеру було віднесено 16 держав
• До другого кластеру віднесено 13 держав
• До третього кластеру віднесено 13 держав
• До четвертого кластеру віднесено 8 держав

Ми можемо візуалізувати кластери на діаграмі розсіювання, яка відображає перші два головних компоненти на осях за допомогою функції fivz_cluster() :

 #plot results of final k-means model
fviz_cluster(km, data = df)

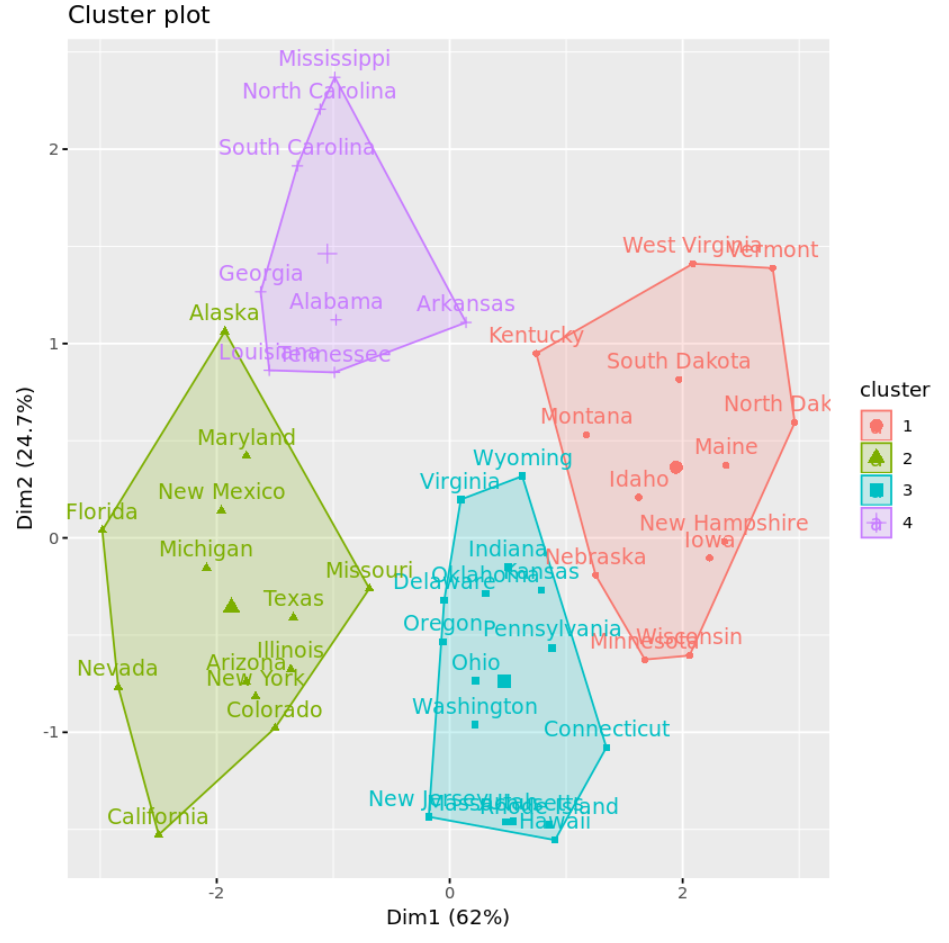
Ми також можемо використовувати функцію Aggregate() , щоб знайти середнє значення змінних у кожному кластері:

 #find means of each cluster
aggregate(USArrests, by= list (cluster=km$cluster), mean)

cluster Murder Assault UrbanPop Rape
				
1 3.60000 78.53846 52.07692 12.17692
2 10.81538 257.38462 76.00000 33.19231
3 5.65625 138.87500 73.87500 18.78125
4 13.93750 243.62500 53.75000 21.41250

Ми інтерпретуємо цей вихід таким чином:

• Середня кількість вбивств на 100 000 громадян серед штатів групи 1 становить 3,6 .
• Середня кількість нападів на 100 000 громадян серед штатів групи 1 становить 78,5 .
• Середній відсоток жителів, які проживають у міській місцевості серед штатів групи 1 становить 52,1% .
• Середня кількість зґвалтувань на 100 000 громадян у штатах групи 1 становить 12,2 .

І так далі.

Ми також можемо додати кластерні призначення кожного стану до вихідного набору даних:

 #add cluster assignment to original data
final_data <- cbind(USArrests, cluster = km$cluster)

#view final data
head(final_data)

	Murder Assault UrbanPop Rape cluster
				
Alabama 13.2 236 58 21.2 4
Alaska 10.0 263 48 44.5 2
Arizona 8.1 294 80 31.0 2
Arkansas 8.8 190 50 19.5 4
California 9.0 276 91 40.6 2
Colorado 7.9 204 78 38.7 2

Переваги та недоліки кластеризації K-Means

Кластеризація K-means пропонує такі переваги:

• Це швидкий алгоритм.
• Він може добре обробляти великі набори даних.

Однак він має такі потенційні недоліки:

• Це вимагає від нас вказати кількість кластерів перед запуском алгоритму.
• Він чутливий до викидів.

Двома альтернативами кластеризації k-середніх є кластеризація k-середніх та ієрархічна кластеризація.

Ви можете знайти повний код R, використаний у цьому прикладі , тут .