Як виконати тест крускала-уолліса в spss

Критерій Крускала-Уолліса використовується для визначення того, чи існує статистично значуща різниця між медіанами трьох або більше незалежних груп. Це вважається непараметричним еквівалентом одностороннього дисперсійного аналізу .

У цьому посібнику пояснюється, як виконати тест Крускала-Уолліса в SPSS.

Приклад: тест Крускала-Уолліса в SPSS

Дослідник хоче знати, чи три препарати по-різному впливають на біль у колінах. Тож він набирає 30 людей, які відчувають подібний біль у колінах, і випадковим чином ділить їх на три групи, які отримують препарат 1, препарат 2 або препарат 3.

Після місяця прийому препарату дослідник просить кожного оцінити біль у коліні за шкалою від 1 до 100, де 100 означає найсильніший біль. Оцінки 30 осіб представлені нижче:

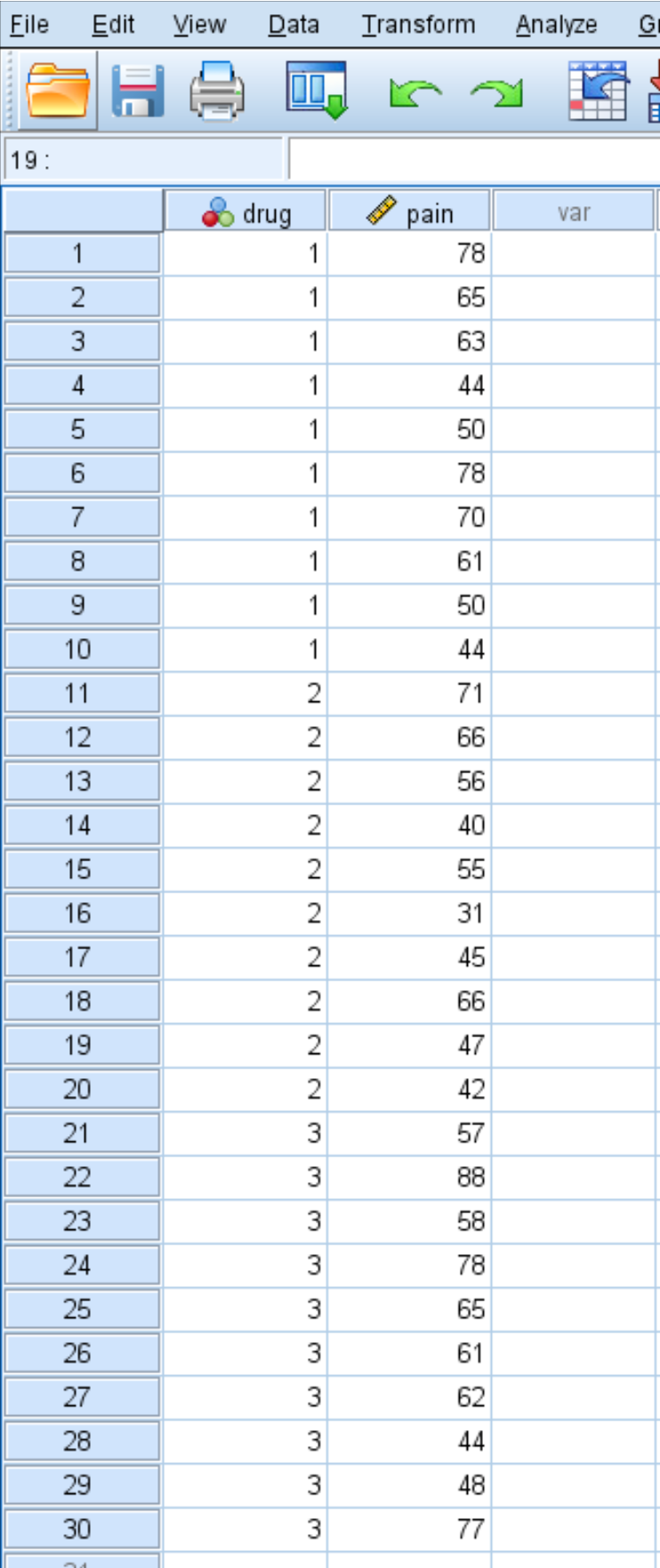
Виконайте такі кроки, щоб виконати тест Крускала-Уолліса, щоб визначити, чи є різниця в рівнях болю в колінах між трьома групами:

Крок 1: Виконайте тест Крускала-Уолліса.

Клацніть вкладку «Аналіз» , потім «Непараметричні тести» , потім «Застарілі діалоги» , а потім «К незалежних зразків» :

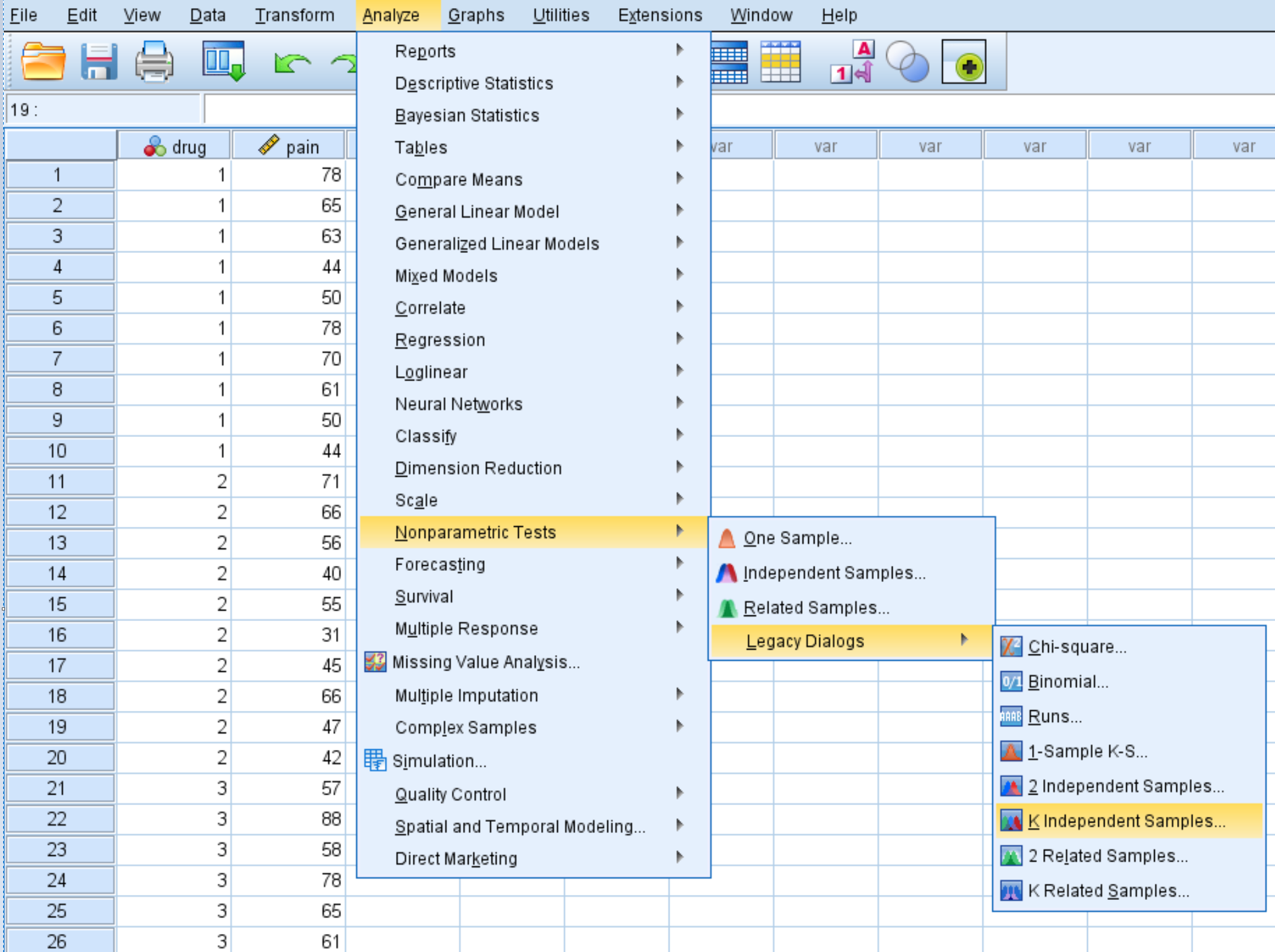
У вікні, що з’явиться, перетягніть змінну болю в поле з позначкою «Список тестових змінних і препарат» у поле з позначкою «Змінна групування». Потім натисніть «Установити діапазон» і встановіть мінімальне значення 1, а максимальне значення — 3. Потім натисніть «Продовжити» . Переконайтеся, що прапорець Kruskal-Wallis H позначено, а потім натисніть OK .

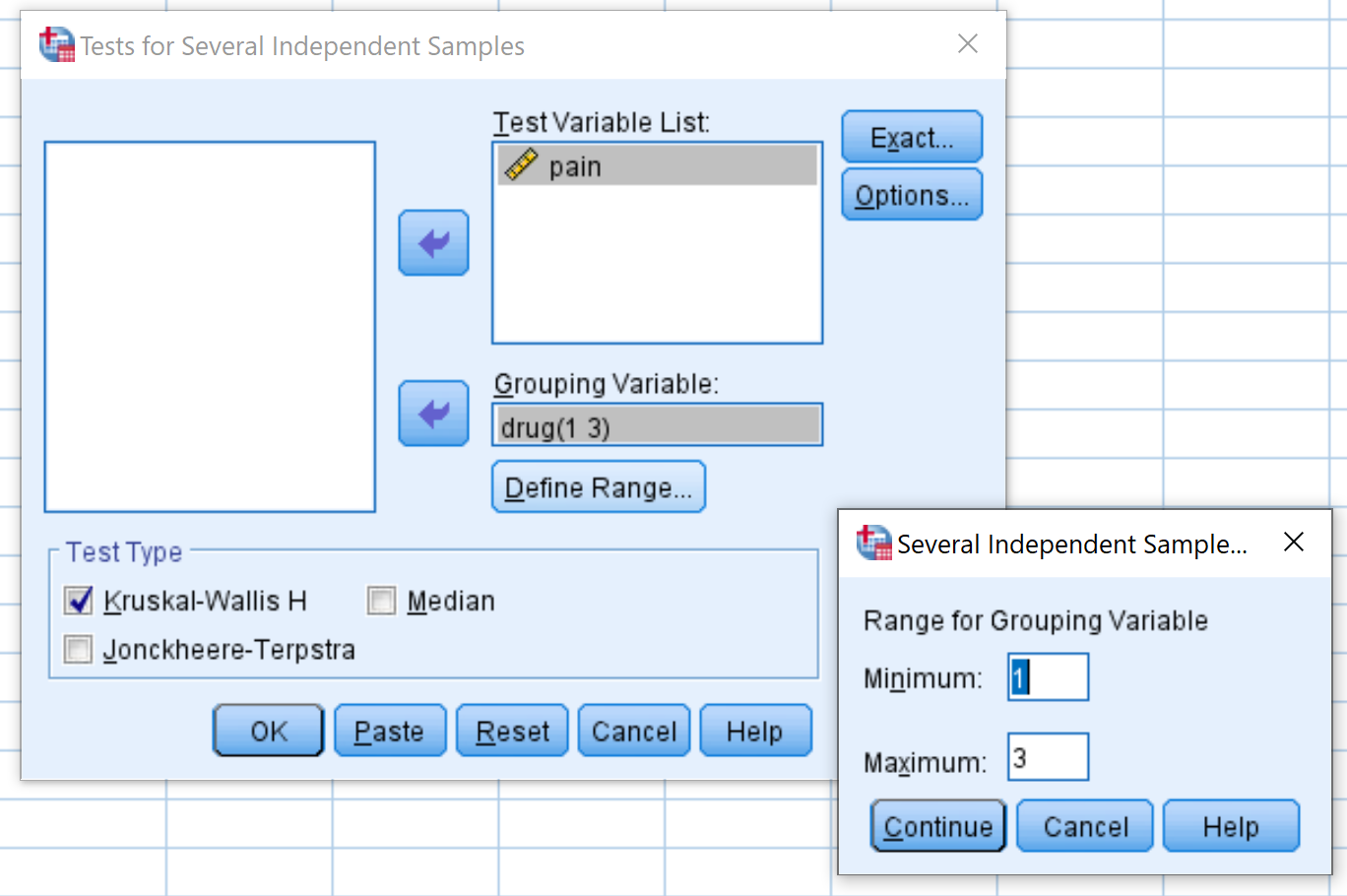
Крок 2: Інтерпретація результатів.

Після натискання кнопки OK з’являться результати тесту Крускала-Уолліса:

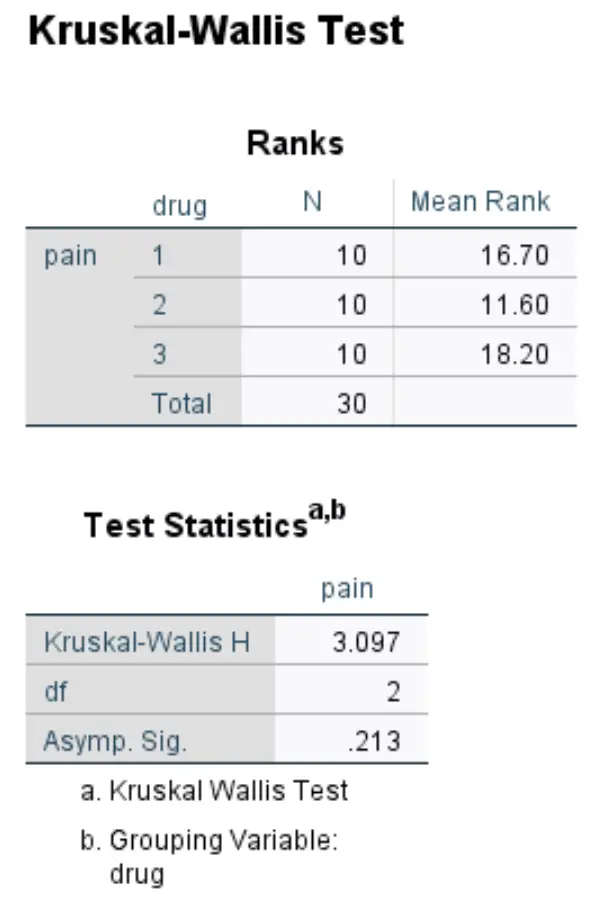
Друга таблиця у вихідних даних відображає результати тесту:

• Краскал-Уолліс Х: Це статистика тесту X ² .
• df: Це ступені свободи, обчислені як #groups-1 = 3-1 = 2.
• Асимп. Sig: це p-значення, пов’язане зі статистикою тесту X ² 3,097 із 2 ступенями свободи. Це також можна знайти за допомогою калькулятора співвідношення хі-квадрат до P-value.

Оскільки p-значення (0,213) не менше 0,05, ми не можемо відхилити нульову гіпотезу. У нас немає достатніх доказів, щоб стверджувати, що існує статистично значуща різниця в оцінках болю в колінах між цими трьома групами.