Як виконати тест крускала-уолліса в stata

Критерій Крускала-Уолліса використовується для визначення того, чи існує статистично значуща різниця між медіанами трьох або більше незалежних груп. Це вважається непараметричним еквівалентом одностороннього дисперсійного аналізу .

Цей посібник пояснює, як виконати тест Крускала-Уолліса в Stata.

Як виконати тест Крускала-Уолліса в Stata

Для цього прикладу ми використаємо набір даних перепису населення , який містить дані перепису 1980 року для всіх п’ятдесяти штатів Сполучених Штатів. У наборі даних штати поділяються на чотири різні регіони:

• Nord Est
• Північний Центральний
• Південь
• Захід

Ми виконаємо тест Крускала-Уолліса, щоб визначити, чи середній вік однаковий у цих чотирьох регіонах.

Крок 1: Завантажте та відобразіть дані.

Спочатку завантажте набір даних, ввівши таку команду в поле команд:

використовуйте https://www.stata-press.com/data/r13/census

Отримайте короткий підсумок набору даних за допомогою такої команди:

узагальнити

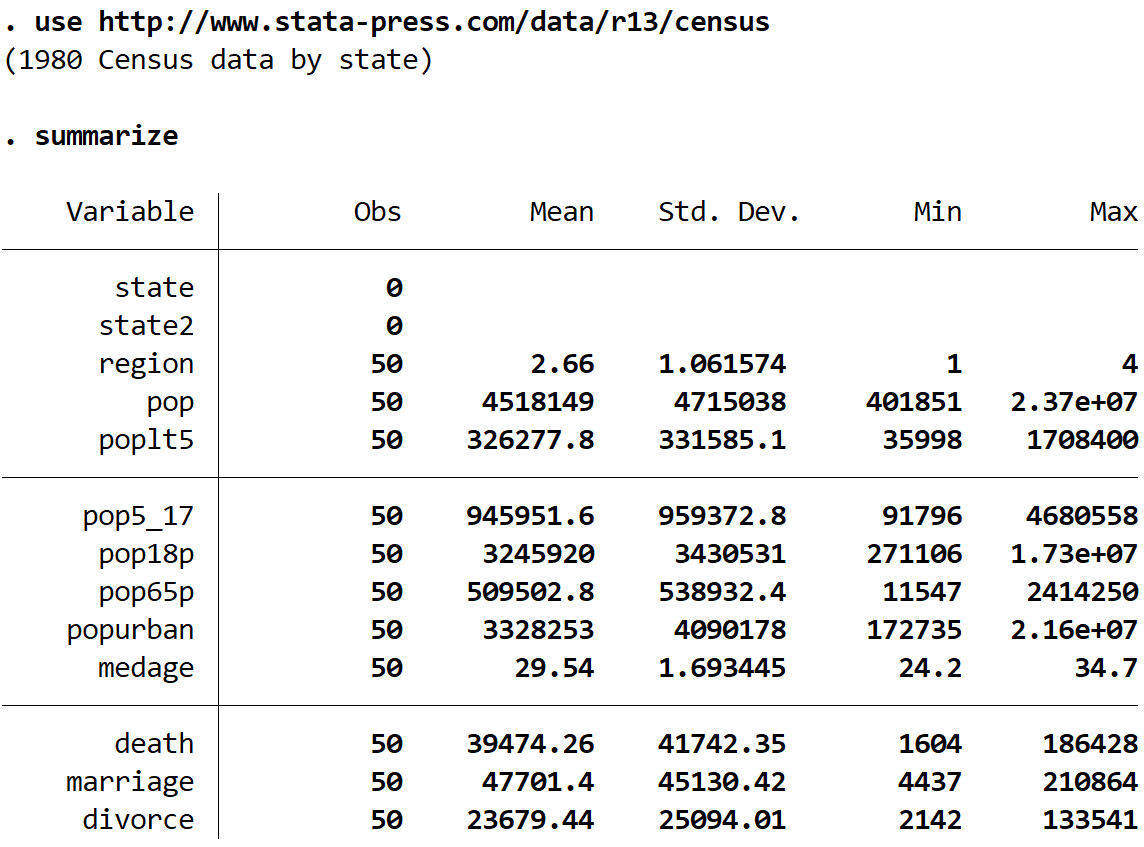
Ми бачимо, що в цьому наборі даних є 13 різних змінних, але ми будемо працювати лише з двома, це medage (середній вік) і region .

Крок 2: Візуалізуйте дані.

Перш ніж виконувати тест Крускала-Уолліса, давайте спершу створимо кілька графіків , щоб візуалізувати середній віковий розподіл для кожного з чотирьох регіонів:

графічний блок medage, on (область)

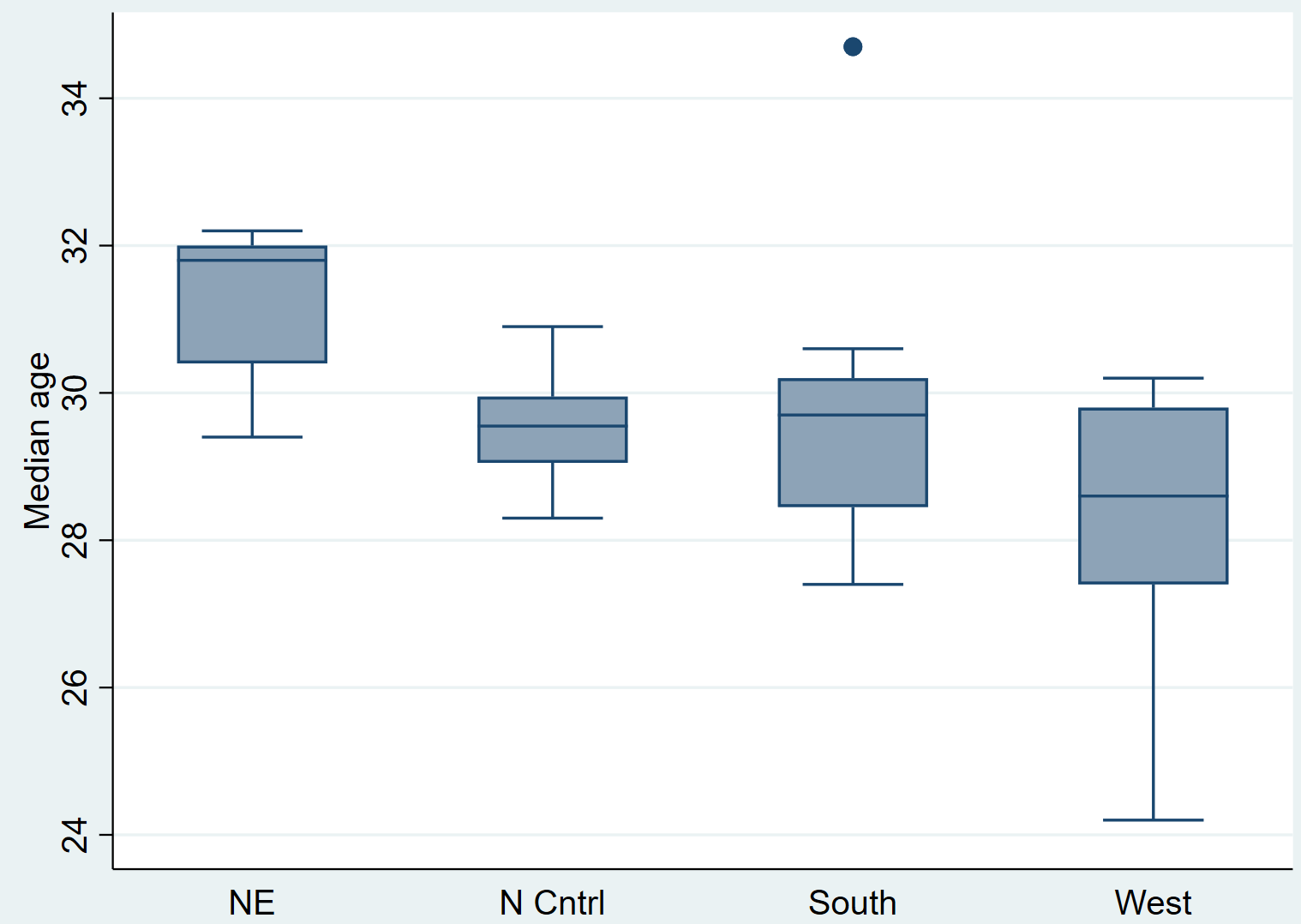
Лише дивлячись на діаграми в коробці, ви можете побачити, що розподіли різняться від регіону до регіону. Потім ми виконаємо тест Крускала-Уолліса, щоб перевірити, чи є ці відмінності статистично значущими.

Крок 3: Виконайте тест Крускала-Уолліса.

Щоб виконати тест Крускала-Уолліса, використовуйте такий синтаксис:

змінна_міри kwallis, за (змінна_групування)

У нашому випадку ми будемо використовувати такий синтаксис:

kwallis medage, за (регіон)

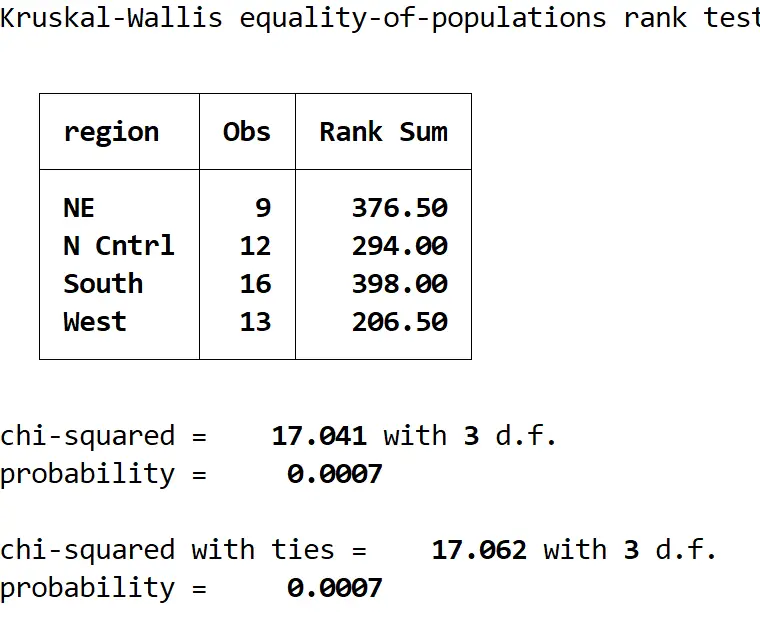
Ось як інтерпретувати результат:

Підсумкова таблиця: у цій таблиці показано кількість спостережень за регіоном і підсумкові рейтинги для кожного регіону.

Хі-квадрат із зв’язками: це значення тестової статистики, яке виявляється 17,062.

ймовірність: це p-значення, яке відповідає тестовій статистиці, яка дорівнює 0,0007. Оскільки це значення менше 0,05, ми можемо відхилити нульову гіпотезу та зробити висновок, що середній вік не є однаковим у чотирьох регіонах.

Крок 4: Повідомте про результати.

Нарешті, ми хотіли б повідомити результати тесту Крускала-Уолліса. Ось приклад того, як це зробити:

Було проведено тест Крускала-Уолліста, щоб визначити, чи був середній вік людей однаковим у наступних чотирьох регіонах Сполучених Штатів:

• Північний схід (n=9)
• Північний Центральний (n=12)
• Південь (n=16)
• Захід (n=13)

Тест показав, що середній вік осіб не був однаковим (X ² = 17,062, p = 0,0007) у чотирьох регіонах. Тобто була статистично значуща різниця в середньому віці між двома чи більше регіонами.