Як використовувати функцію lm() у r для підгонки лінійних моделей

Функція lm() у R використовується для підгонки моделей лінійної регресії.

Ця функція використовує такий базовий синтаксис:

lm(формула, дані, …)

золото:

• формула: формула лінійної моделі (наприклад, y ~ x1 + x2)
• дані: назва блоку даних, який містить дані

У наведеному нижче прикладі показано, як використовувати цю функцію в R для виконання наступних дій:

• Підібрати регресійну модель
• Переглянути зведення регресійної моделі
• Перегляд діагностичних графіків моделі
• Побудуйте графік адаптованої моделі регресії
• Робіть прогнози за допомогою регресійної моделі

Підберіть модель регресії

У наведеному нижче коді показано, як використовувати функцію lm() для підгонки моделі лінійної регресії в R:

 #define data
df = data. frame (x=c(1, 3, 3, 4, 5, 5, 6, 8, 9, 12),
                y=c(12, 14, 14, 13, 17, 19, 22, 26, 24, 22))

#fit linear regression model using 'x' as predictor and 'y' as response variable
model <- lm(y ~ x, data=df)

Показати зведення моделі регресії

Потім ми можемо використати функцію summary() , щоб відобразити підсумок відповідності моделі регресії:

 #view summary of regression model
summary(model)

Call:
lm(formula = y ~ x, data = df)

Residuals:
    Min 1Q Median 3Q Max 
-4.4793 -0.9772 -0.4772 1.4388 4.6328 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 11.1432 1.9104 5.833 0.00039 ***
x 1.2780 0.2984 4.284 0.00267 ** 
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 2.929 on 8 degrees of freedom
Multiple R-squared: 0.6964, Adjusted R-squared: 0.6584 
F-statistic: 18.35 on 1 and 8 DF, p-value: 0.002675

Ось як інтерпретувати найважливіші значення в моделі:

• F-статистика = 18,35, відповідне p-значення = 0,002675. Оскільки це p-значення менше 0,05, модель в цілому є статистично значущою.
• Кратне R у квадраті = 0,6964. Це говорить нам про те, що 69,64% варіацій у змінній відповіді, y, можна пояснити змінною-предиктором, x.
• Розрахунковий коефіцієнт x : 1,2780. Це говорить нам про те, що кожне додаткове збільшення x пов’язане із середнім збільшенням y на 1,2780.

Потім ми можемо використати оцінки коефіцієнтів із вихідних даних, щоб написати розрахункове рівняння регресії:

y = 11,1432 + 1,2780*(x)

Бонус : тут ви можете знайти повний посібник з інтерпретації кожного значення результату регресії в R.

Перегляд діагностичних графіків моделі

Потім ми можемо використовувати функцію plot() для побудови діагностичних графіків регресійної моделі:

 #create diagnostic plots
plot(model) 

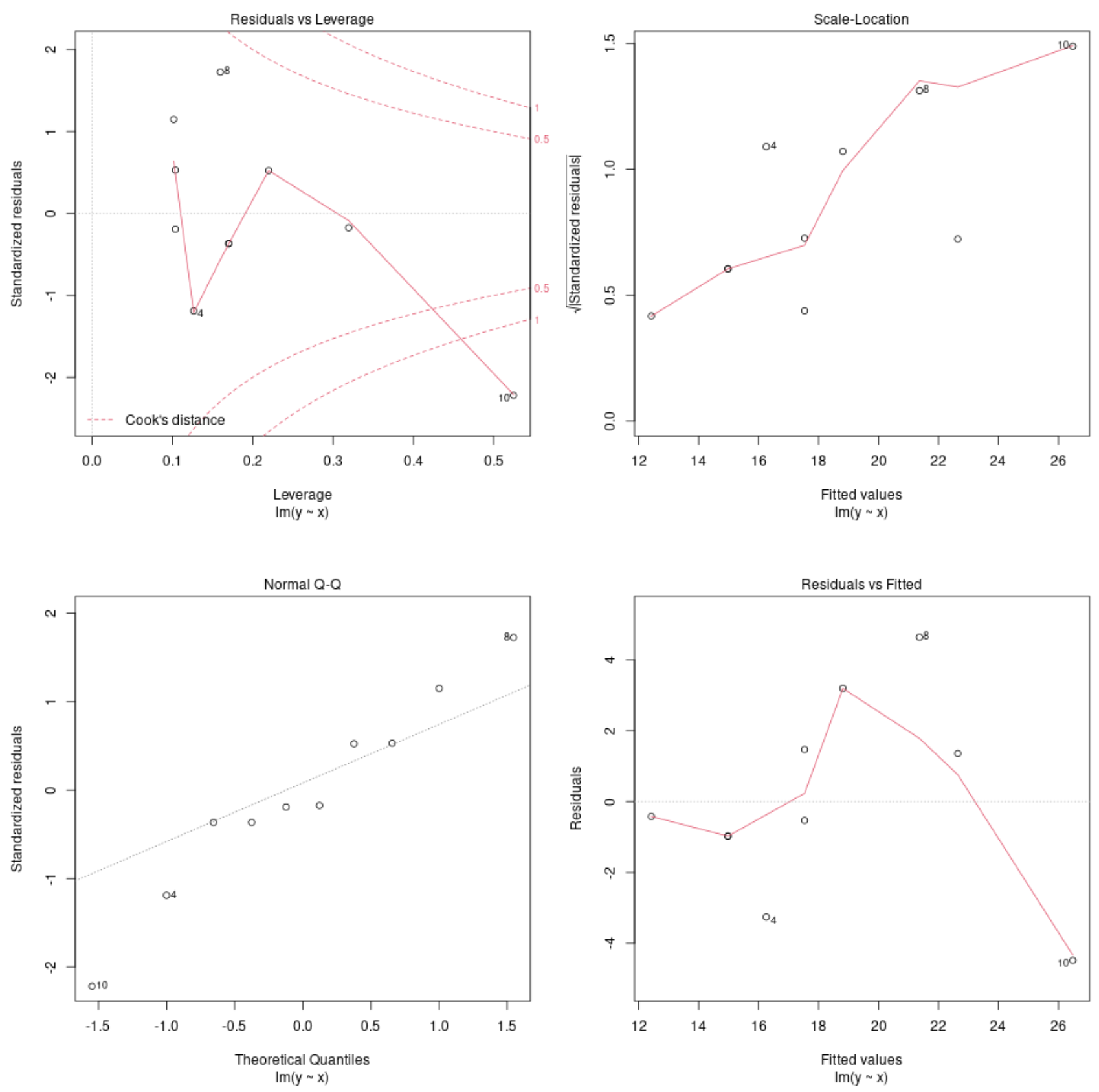
Ці графіки дозволяють нам аналізувати залишки регресійної моделі, щоб визначити, чи підходить модель для використання з даними.

Зверніться до цього підручника , щоб отримати повне пояснення того, як інтерпретувати діаграми діагностики моделі в R.

Побудуйте графік адаптованої моделі регресії

Ми можемо використати функцію abline() , щоб побудувати модель підігнаної регресії:

 #create scatterplot of raw data
plot(df$x, df$y, col=' red ', main=' Summary of Regression Model ', xlab=' x ', ylab=' y ')

#add fitted regression line
abline(model)

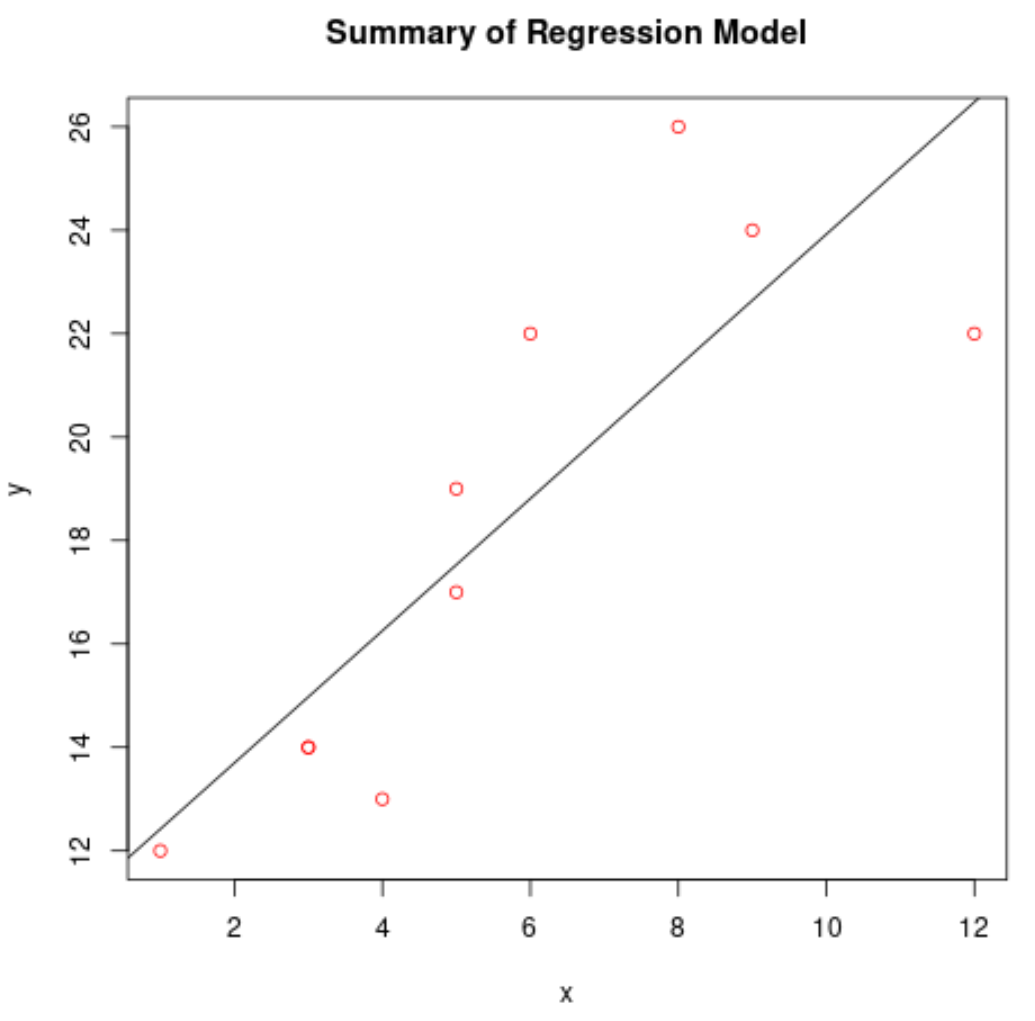
Використовуйте регресійну модель для прогнозування

Ми можемо використовувати функцію predict() , щоб передбачити значення відповіді для нового спостереження:

 #define new observation
new <- data. frame (x=c(5))

#use the fitted model to predict the value for the new observation
predict(model, newdata = new)

      1 
17.5332

Модель передбачає, що це нове спостереження матиме значення відповіді 17,5332 .

Додаткові ресурси

Як виконати просту лінійну регресію в R
Як виконати множинну лінійну регресію в R
Як виконати покрокову регресію в R