Як виконати тест log rank у r

Тест логарифмічного рангу є найпоширенішим способом порівняння кривих виживання між двома групами.

У цьому тесті використовуються такі припущення :

H ₀ : Немає різниці у виживанні між двома групами.

H _A : Існує різниця у виживанні між двома групами.

Якщо p-значення тесту нижче певного рівня значущості (наприклад, α = 0,05), тоді ми можемо відхилити нульову гіпотезу та зробити висновок, що є достатньо доказів, щоб стверджувати, що існує різниця у виживанні між двома групами.

Щоб виконати перевірку логарифмічного рангу в R, ми можемо використати функцію survdiff() із пакета survival , яка використовує такий синтаксис:

survdiff(Surv(час, статус) ~ предиктори, дані)

Ця функція повертає статистику хі-квадрат і відповідне значення p.

У наступному прикладі показано, як використовувати цю функцію для виконання перевірки логарифмічного рангу в R.

Приклад: Log Rank Test у R

Для цього прикладу ми використаємо набір даних про яєчники з пакету виживання . Цей набір даних містить таку інформацію про 26 пацієнтів:

• Тривалість життя (у місяцях) після діагностики раку яєчників
• Незалежно від того, чи був час виживання цензурований
• Тип отриманого лікування (rx = 1 або rx = 2)

Наступний код показує, як відобразити перші шість рядків цього набору даних:

 library (survival)

#view first six rows of dataset
head(ovarian)

  futime fustat age resid.ds rx ecog.ps
1 59 1 72.3315 2 1 1
2 115 1 74.4932 2 1 1
3 156 1 66.4658 2 1 2
4 421 0 53.3644 2 2 1
5,431 1 50.3397 2 1 1
6 448 0 56.4301 1 1 2

У наведеному нижче коді показано, як виконати логарифмічно-ранговий тест, щоб визначити, чи є різниця у виживаності між пацієнтами, які отримували різні види лікування:

 #perform log rank test
survdiff(Surv(futime, fustat) ~ rx, data=ovarian)

Call:
survdiff(formula = Surv(futime, fustat) ~ rx, data = ovarian)

      N Observed Expected (OE)^2/E (OE)^2/V
rx=1 13 7 5.23 0.596 1.06
rx=2 13 5 6.77 0.461 1.06

 Chisq= 1.1 on 1 degrees of freedom, p= 0.3 

Статистика тесту хі-квадрат становить 1,1 з 1 ступенем свободи, а відповідне значення p становить 0,3 . Оскільки це p-значення не менше 0,05, ми не можемо відхилити нульову гіпотезу.

Іншими словами, ми не маємо достатніх доказів, щоб стверджувати, що існує статистично значуща різниця у виживаності між двома методами лікування.

Ми також можемо побудувати криві виживання для кожної групи, використовуючи такий синтаксис:

 #plot survival curves for each treatment group
plot(survfit(Surv(futime, fustat) ~ rx, data = ovarian), 
     xlab = " Time ", 
     ylab = “ Overall survival probability ”)

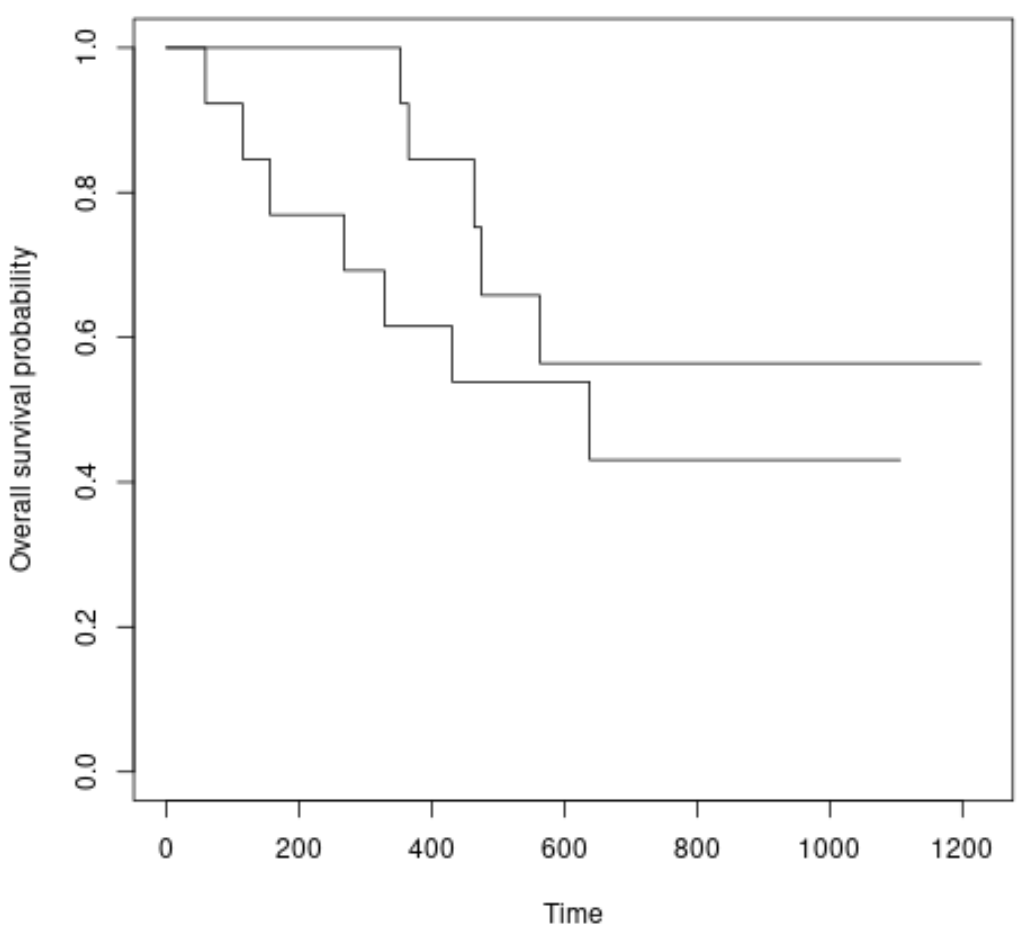
Ми бачимо, що криві виживання дещо відрізняються, але логарифмічний тест показав нам, що різниця не є статистично значущою.