Mae проти rmse: який показник вам слід використовувати?

Регресійні моделі використовуються для кількісного визначення зв’язку між однією або декількома змінними предиктора та змінною відповіді .

Щоразу, коли ми підбираємо регресійну модель, ми хочемо зрозуміти, наскільки добре модель здатна використовувати значення змінних предикторів для прогнозування значення змінної відповіді.

Двома показниками, які ми часто використовуємо для кількісного визначення того, наскільки добре модель відповідає набору даних, є середня абсолютна помилка (MAE) і середньоквадратична помилка (RMSE), які обчислюються таким чином:

MAE : показник, який повідомляє нам про середню абсолютну різницю між прогнозованими значеннями та фактичними значеннями в наборі даних. Чим нижчий MAE, тим краще модель відповідає набору даних.

MAE = 1/n * Σ|y _i – ŷ _i |

золото:

• Σ – символ, що означає «сума»
• y _i – спостережуване значення для ^i-го спостереження
• ŷ _i – прогнозоване значення для i- ^го спостереження
• n – розмір вибірки

RMSE : метрика, яка повідомляє нам квадратний корінь із середньоквадратичної різниці між прогнозованими значеннями та фактичними значеннями в наборі даних. Чим нижче RMSE, тим краще модель відповідає набору даних.

Він розраховується таким чином:

RMSE = √ Σ(y _i – ŷ _i ) ² / n

золото:

• Σ – символ, що означає «сума»
• ŷ _i – прогнозоване значення для i- ^го спостереження
• y _i – спостережуване значення для ^i-го спостереження
• n – розмір вибірки

Приклад: Розрахунок RMSE і MAE

Припустімо, ми використовуємо регресійну модель, щоб передбачити, скільки очок наберуть 10 гравців у баскетбольній грі.

У наведеній нижче таблиці наведено очки, передбачені моделлю, у порівнянні з фактичними очками, набраними гравцями:

Використовуючи калькулятор MAE, ми можемо розрахувати, що MAE становить 3,2.

Це говорить нам про те, що середня абсолютна різниця між значеннями, передбаченими моделлю, і фактичними значеннями становить 3,2.

Використовуючи калькулятор RMSE , ми можемо обчислити, що RMSE дорівнює 4 .

Це говорить нам про те, що квадратний корінь із середньоквадратичної різниці між прогнозованими набраними балами та фактичними набраними балами дорівнює 4.

Зауважте, що кожна метрика дає нам уявлення про типову різницю між прогнозованим значенням, зробленим моделлю, та фактичним значенням у наборі даних, але інтерпретація кожного показника дещо відрізняється.

RMSE проти MAE: який показник вам слід використовувати?

Якщо ви хочете призначити більшу вагу спостереженням, які знаходяться далі від середнього (тобто якщо відхилення 20 більш ніж удвічі гірше, ніж відхилення 10), краще використовувати RMSE для вимірювання помилки, оскільки RMSE є більш чутливі до спостережень, що знаходяться далі від середнього.

Однак, якщо бути «зсувом» на 20 вдвічі гірше, ніж бути «зсувом» на 10, тоді краще використовувати MAE.

Щоб проілюструвати це, припустімо, що у нас є гравець, який явно виділяється за кількістю набраних очок:

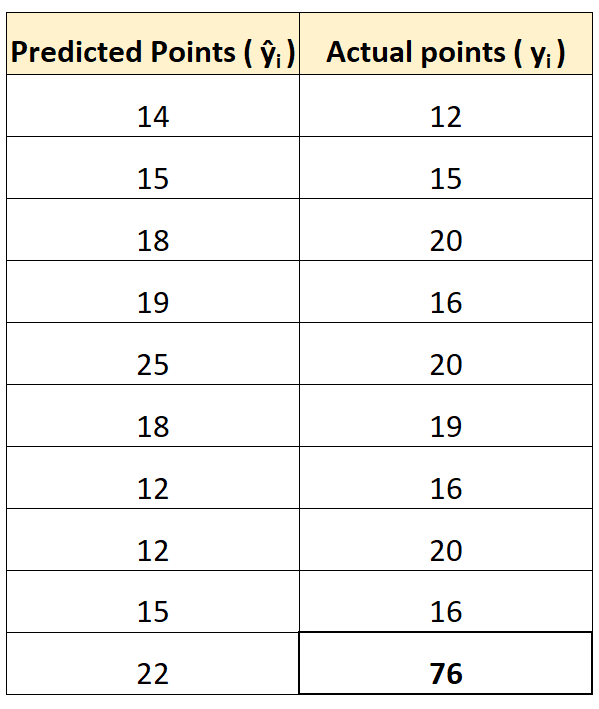
Використовуючи згадані раніше онлайн-калькулятори, ми можемо розрахувати MAE та RMSE як:

• MAE : 8
• RMSE : 16,4356

Зверніть увагу, що RMSE збільшується набагато більше, ніж MAE.

Це тому, що RMSE використовує квадрати різниць у своїй формулі, а квадрат різниці між спостережуваним значенням 76 і прогнозованим значенням 22 досить великий. Це призводить до значного збільшення значення RMSE.

На практиці ми зазвичай підбираємо кілька регресійних моделей до набору даних і обчислюємо лише один із цих показників для кожної моделі.

Наприклад, ми могли б підібрати три різні моделі регресії та обчислити RMSE для кожної моделі. Потім ми виберемо модель із найнижчим значенням RMSE як «найкращу», оскільки саме вона робить прогнози найближчими до фактичних значень у наборі даних.

У будь-якому випадку переконайтеся, що ви обчислюєте однаковий показник для кожної моделі. Наприклад, не обчислюйте MAE для однієї моделі та RMSE для іншої моделі, а потім порівнюйте ці два вимірювання.

Додаткові ресурси

У наступних посібниках пояснюється, як розрахувати MAE за допомогою різного статистичного програмного забезпечення:

Як обчислити середню абсолютну похибку в Excel
Як обчислити середню абсолютну похибку в R
Як обчислити середню абсолютну похибку в Python

У наступних посібниках пояснюється, як розрахувати RMSE за допомогою різного статистичного програмного забезпечення:

Як обчислити середню квадратичну помилку в Excel
Як обчислити середню квадратичну помилку в R
Як обчислити середню квадратичну помилку в Python