Як обчислити ймовірності normalcdf в excel

Функцію NormalCDF на калькуляторі TI-83 або TI-84 можна використовувати для визначення ймовірності того, що випадкова величина з нормальним розподілом приймає значення в межах певного діапазону.

На калькуляторі TI-83 або TI-84 ця функція використовує такий синтаксис

normalcdf (нижній, верхній, μ, σ)

золото:

• нижчий = нижче значення діапазону
• upper = верхнє значення діапазону
• μ = середнє значення популяції
• σ = стандартне відхилення сукупності

Наприклад, припустимо, що випадкова змінна зазвичай розподілена із середнім значенням 50 і стандартним відхиленням 4. Імовірність того, що випадкова змінна набере значення від 48 до 52, можна обчислити наступним чином:

normalcdf(48, 52, 50, 4) = 0,3829

Ми можемо відтворити цю відповідь у Excel за допомогою функції NORM.DIST() , яка використовує такий синтаксис:

NORM.DIST(x, σ, μ, сукупний)

золото:

• x = індивідуальне значення даних
• μ = середнє значення популяції
• σ = стандартне відхилення сукупності
• кумулятивний = FALSE обчислення PDF; TRUE обчислює CDF

Наступні приклади показують, як використовувати цю функцію на практиці.

Приклад 1: Імовірність між двома значеннями

Припустимо, що випадкова змінна має нормальний розподіл із середнім значенням 50 і стандартним відхиленням 4. Імовірність того, що випадкова змінна набере значення від 48 до 52, можна обчислити таким чином:

 =NORM. DIST (52, 50, 4, TRUE ) - NORM. DIST (48, 50, 4, TRUE )

На наступному зображенні показано, як виконати цей обчислення в Excel:

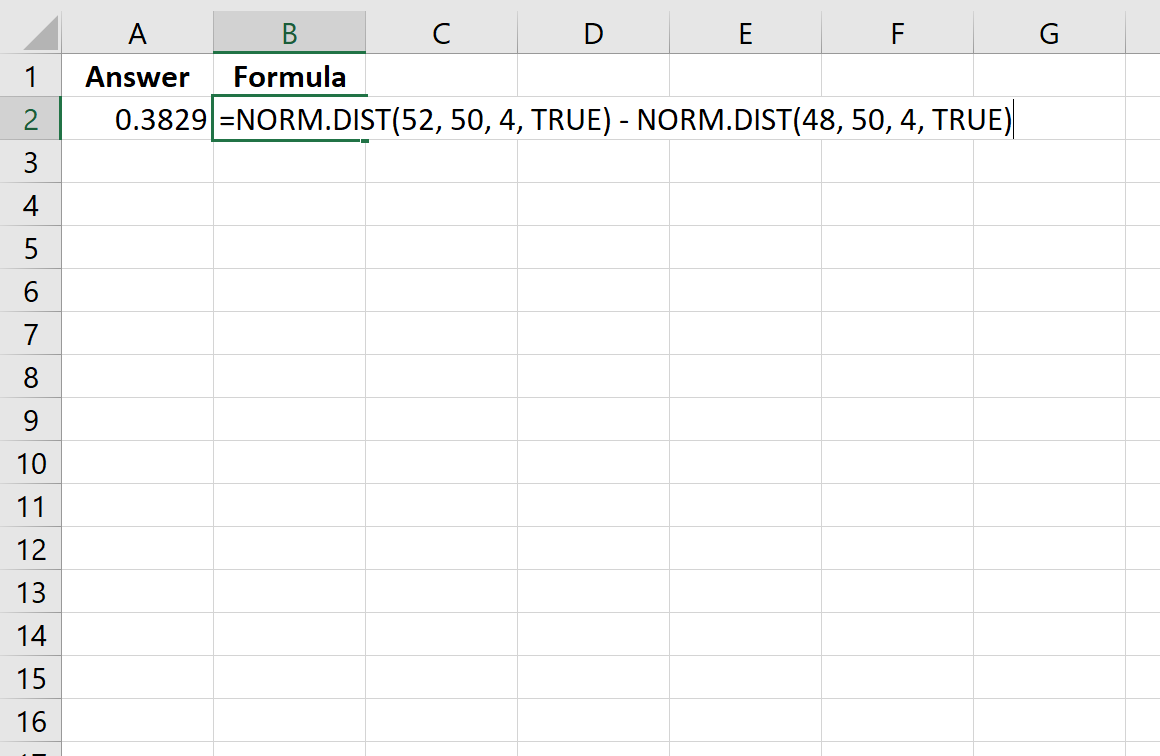
Ймовірність виявляється рівною 0,3829.

Приклад 2: Імовірність менше одного значення

Припустимо, що випадкова змінна має нормальний розподіл із середнім значенням 50 і стандартним відхиленням 4. Імовірність того, що випадкова змінна набере значення менше 48, можна обчислити наступним чином:

 =NORM. DIST (48, 50, 4, TRUE )

На наступному зображенні показано, як виконати цей обчислення в Excel:

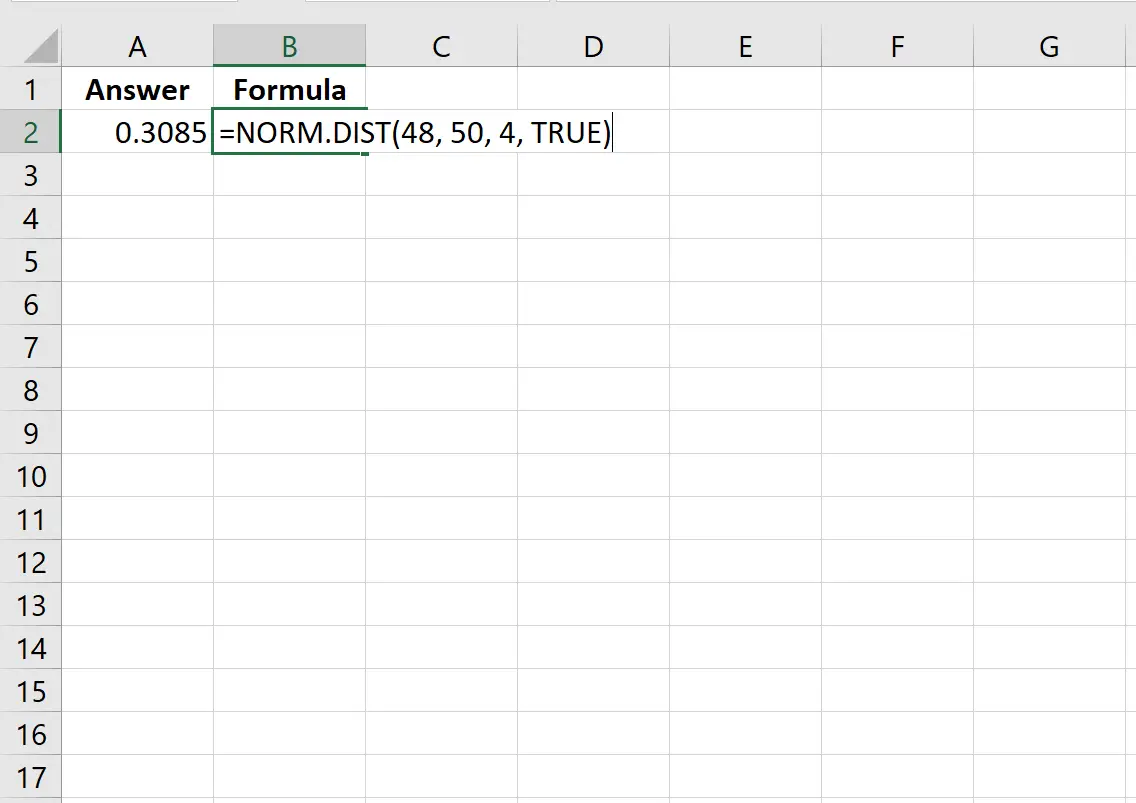
Ймовірність виявляється рівною 0,3085.

Приклад 3: ймовірність більша за значення

Припустимо, що випадкова змінна має нормальний розподіл із середнім значенням 50 і стандартним відхиленням 4. Імовірність того, що випадкова змінна набере значення більше 55, можна обчислити таким чином:

 =1 - NORM. DIST (55, 50, 4, TRUE )

На наступному зображенні показано, як виконати цей обчислення в Excel:

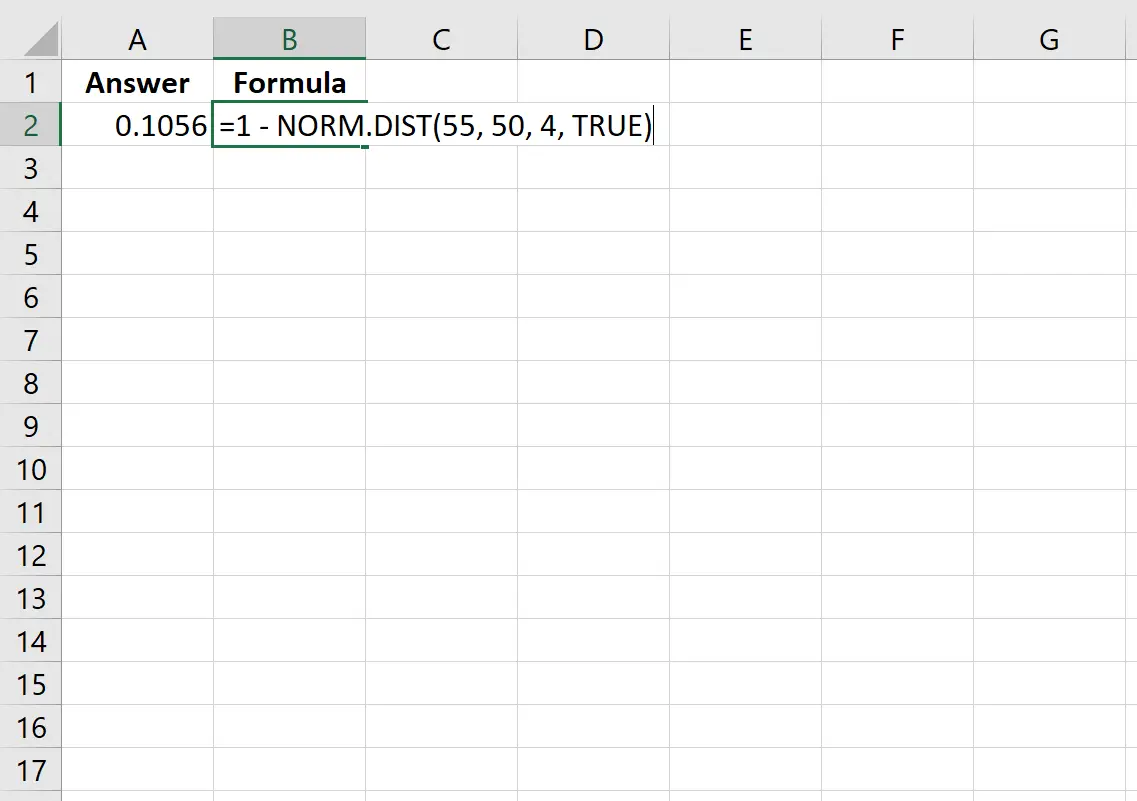
Ймовірність виявляється рівною 0,1056.

Додаткові ресурси

Ви також можете використовувати цей звичайний калькулятор CDF , щоб автоматично знайти ймовірності, пов’язані з нормальним розподілом.