Як знайти значення p у google таблицях (покроково)

Найпростіший спосіб обчислити p-значення в Google Таблицях — це використовувати функцію T.TEST() , яка знаходить p-значення, пов’язане з t-тестом, і використовує такий синтаксис:

T.TEST (діапазон 1, діапазон 2, хвости, тип)

золото:

• діапазон1: перший зразок даних
• діапазон2: друга вибірка даних
• хвости: кількість хвостів для використання в тесті
  • 1: Однобічний (або «однобічний») t-тест
  • 2: Двосторонній (або «двосторонній) t-тест
• type: тип тесту t
  • 1: Парний t-тест
  • 2: двовибірковий t-критерій з рівною дисперсією
  • 3: T-критерій двох вибірок з нерівною дисперсією

Ця функція повертає значення p, яке відповідає критерію t.

Наступний покроковий приклад показує, як використовувати цю функцію на практиці.

Крок 1: Створіть дані

Спочатку давайте створимо фальшивий набір даних, що містить висоту двох різних видів рослин:

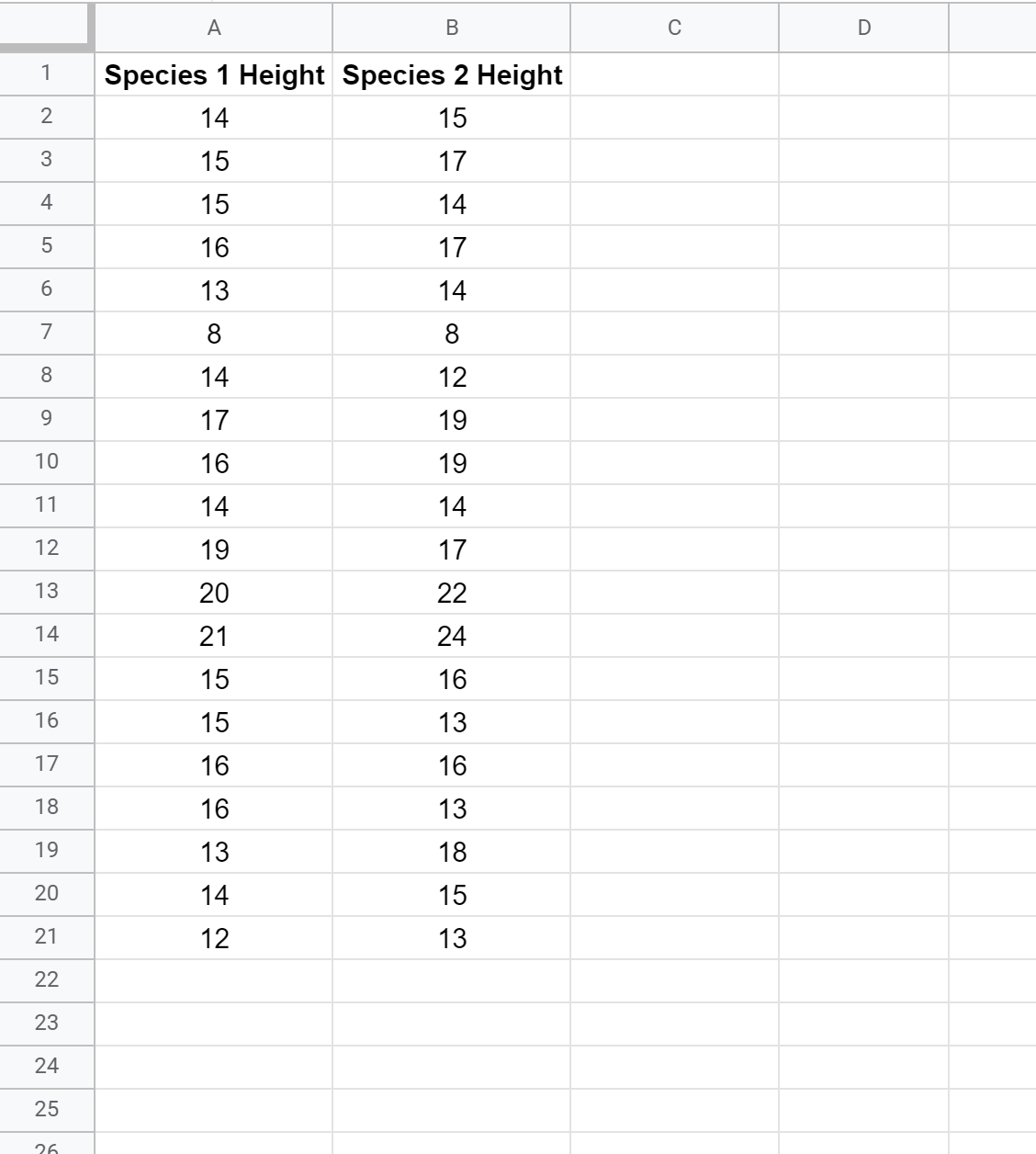
Крок 2: Обчисліть значення P для t-критерію

Далі, скажімо, ми хочемо виконати t-тест, щоб визначити, чи однакова середня висота двох видів рослин.

На наступних знімках екрана показано формули, які слід використовувати для обчислення тестових значень p.

Т-критерій парних вибірок

Ми можемо використати таку формулу, щоб обчислити значення p для t-критерію парних зразків :

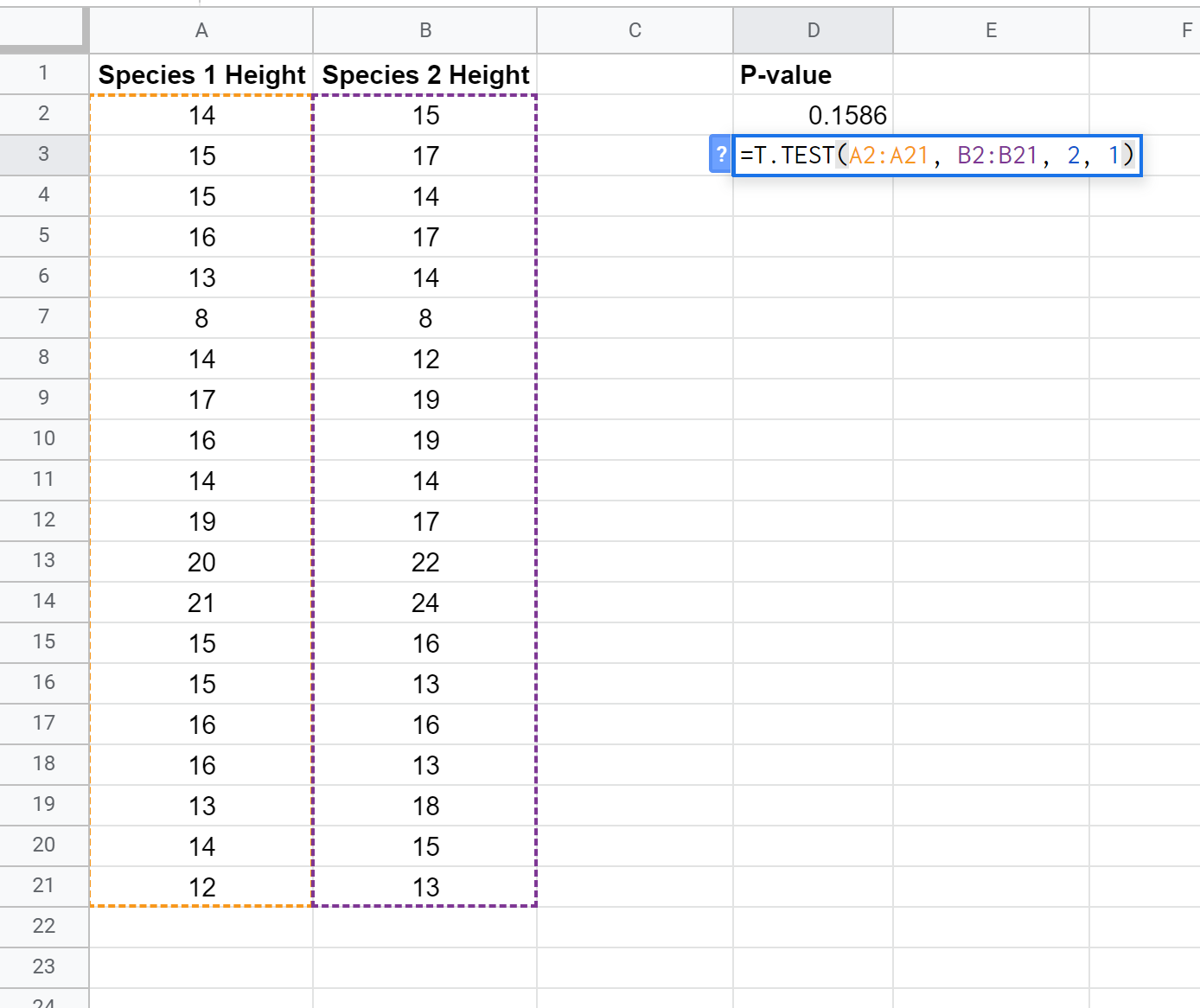
P-значення виявляється рівним 0,1586 . Оскільки це не менше α = 0,05, ми не можемо відхилити нульову гіпотезу тесту. У нас немає достатніх доказів, щоб стверджувати, що середня висота між двома видами різна.

Двовибірковий t-критерій з рівною дисперсією

Ми можемо використати таку формулу, щоб обчислити значення p для t-критерію двох вибірок з однаковою дисперсією:

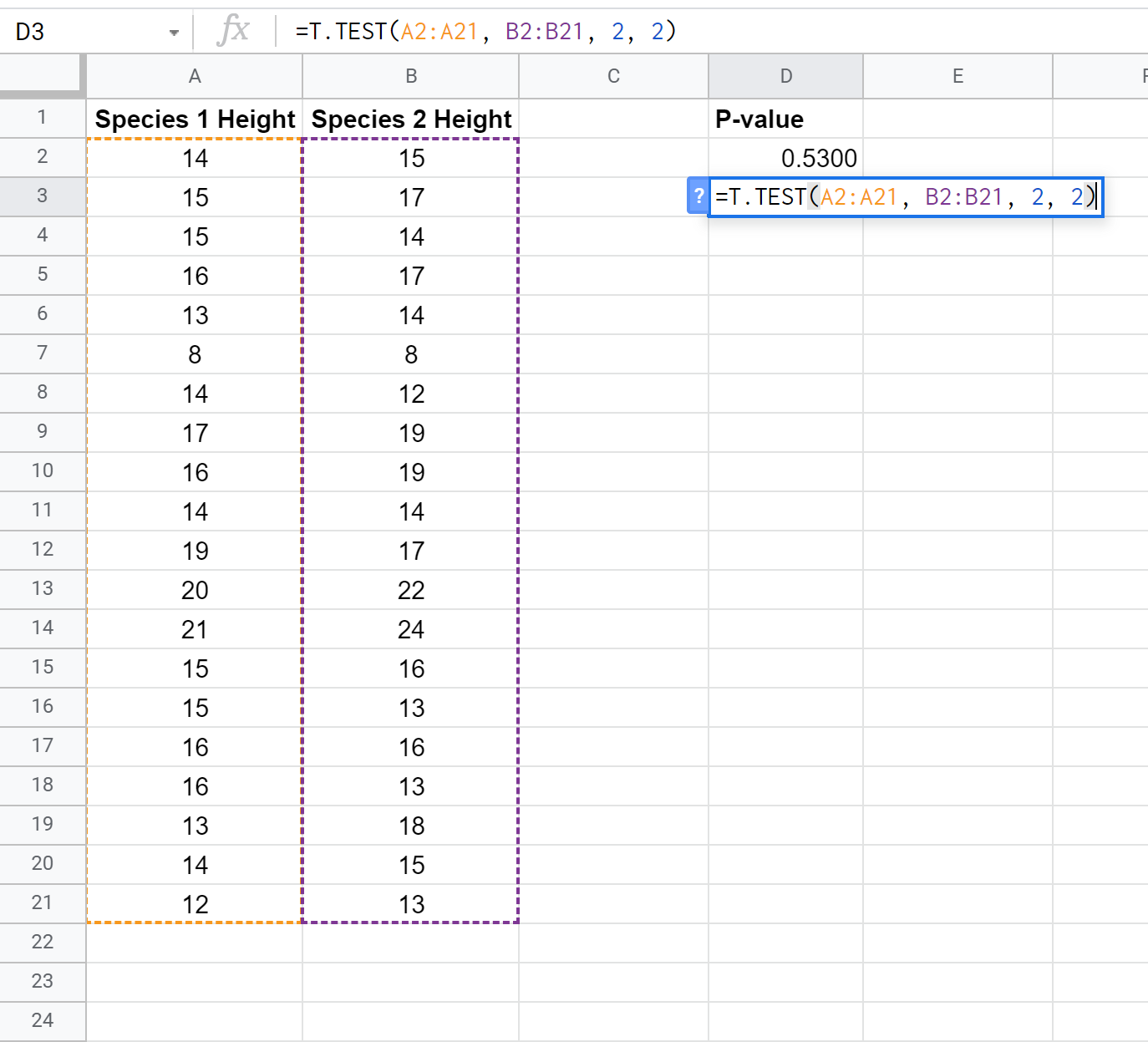
P-значення виявляється рівним 0,5300 . Оскільки це не менше α = 0,05, ми не можемо відхилити нульову гіпотезу тесту. У нас немає достатніх доказів, щоб стверджувати, що середня висота між двома видами різна.

Двовибірковий t-критерій з нерівною дисперсією

Ми можемо використати таку формулу, щоб обчислити значення p для t-критерію двох вибірок із нерівною дисперсією:

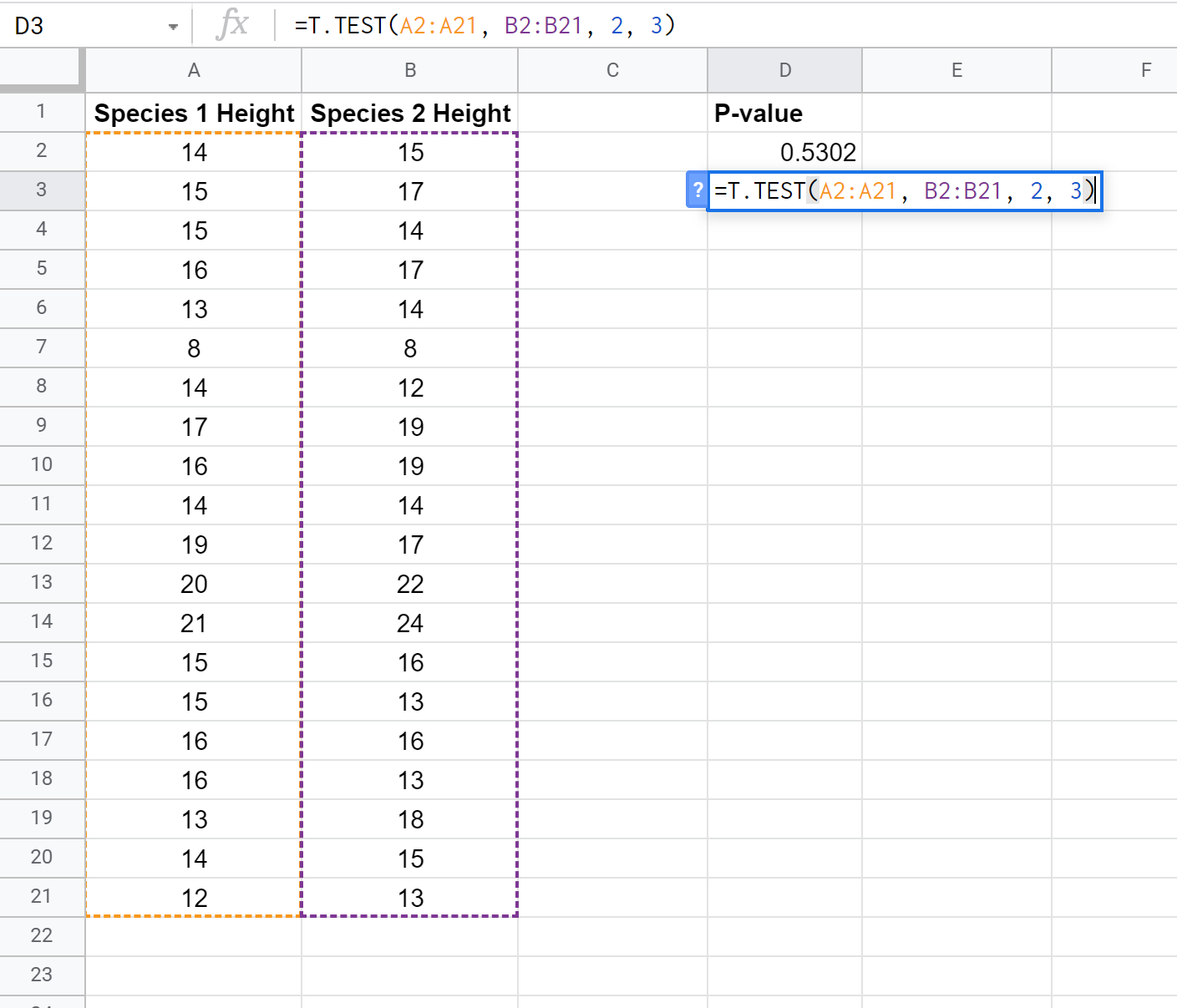
P-значення виявляється рівним 0,5302 . Оскільки це не менше α = 0,05, ми не можемо відхилити нульову гіпотезу тесту. У нас немає достатніх доказів, щоб стверджувати, що середня висота між двома видами різна.

Додаткові ресурси

Пояснення значень P і статистичної значущості
Як виконувати t-тести в Google Таблицях
Як виконати односторонній дисперсійний аналіз у Google Таблицях