Що таке функція ймовірної маси (pmf) у статистиці?
Функція маси ймовірності , часто скорочена PMF , повідомляє нам про ймовірність того, що дискретна випадкова змінна набуває певного значення.
Наприклад, припустімо, що ми один раз кидаємо кубик. Якщо ми позначимо x число, на яке падає кубик, то ймовірність того, що x дорівнює різним значенням, можна описати так:
- P(X=1): 1/6
- P(X=2): 1/6
- P(X=3): 1/6
- P(X=4): 1/6
- P(X=5): 1/6
- P(X=6): 1/6
Існує рівна ймовірність того, що кубик впаде на будь-яке число від 1 до 6.
Ось як ми запишемо ці ймовірності як функцію маси ймовірностей:
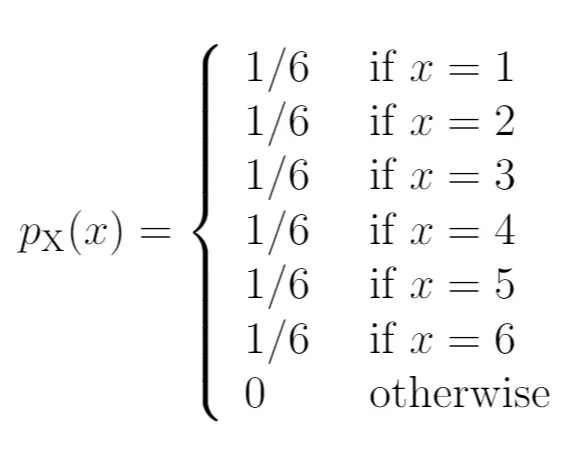
Ліва частина діаграми показує ймовірність, пов’язану з результатами на правій стороні:
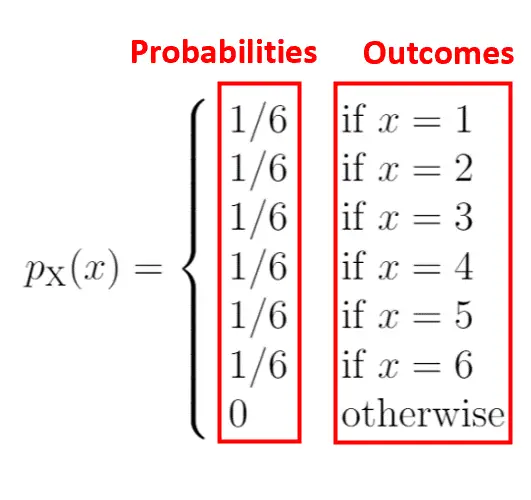
Характеристика функції ймовірнісної маси полягає в тому, що сума всіх ймовірностей повинна дорівнювати 1. Ви помітите, що ця PMF задовольняє цю умову:
Сума ймовірностей = 1/6 + 1/6 + 1/6 + 1/6 + 1/6 + 1/6 = 1.
Підтримка функції маси ймовірності відноситься до набору значень, які може приймати дискретна випадкова величина. У цьому прикладі опорою буде {1, 2, 3, 4, 5, 6}, оскільки значення кубика може мати будь-яке з цих значень.
Поза підтримкою значення PMF дорівнює нулю. Наприклад, ймовірність того, що кубик впаде на «0», «7» або «8», дорівнює нулю, оскільки жодне з цих чисел не включено в дужку.
Функції маси ймовірності на практиці
Два найпоширеніші приклади функцій ймовірнісної маси на практиці стосуються біноміального розподілу та розподілу Пуассона .
Біноміальний розподіл
Якщо випадкова величина X відповідає біноміальному розподілу, то ймовірність успіху X = k можна знайти за такою формулою:
P(X=k) = n C k * p k * (1-p) nk
золото:
- n: кількість випробувань
- k: кількість успіхів
- p: ймовірність успіху в даному випробуванні
- n C k : кількість способів отримати k успіхів у n випробуваннях
Наприклад, припустимо, що ми кидаємо монету 3 рази. Ми можемо використати наведену вище формулу, щоб визначити ймовірність отримати 0, 1, 2 і 3 голови в цих 3 підкиданнях:
- P(X=0) = 3 C 0 * 0,5 0 * (1-0,5) 3-0 = 1 * 1 * (0,5) 3 = 0,125
- P(X=1) = 3 C 1 * 0,5 1 * (1-0,5) 3-1 = 1 * 1 * (0,5) 2 = 0,375
- P(X=2) = 3 C 2 * 0,5 2 * (1-0,5) 3-2 = 1 * 1 * (0,5) 1 = 0,375
- P(X=3) = 3 C 3 * 0,5 3 * (1-0,5) 3-3 = 1 * 1 * (0,5) 0 = 0,125
Розподіл риби
Якщо випадкова величина X відповідає розподілу Пуассона, то ймовірність успіху X = k можна знайти за такою формулою:
P(X=k) = λ k * e – λ / k!
золото:
- λ: середня кількість успіхів протягом певного інтервалу
- k: кількість успіхів
- e: константа, що дорівнює приблизно 2,71828
Наприклад, припустимо, що в одній лікарні в середньому відбувається 2 пологи на годину. Ми можемо використовувати наведену вище формулу, щоб визначити ймовірність народження 0, 1, 2, 3 тощо. в певну годину:
- P(X=0) = 2 0 * e – 2 / 0! = 0,1353
- P(X=1) = 2 1 * e – 2 / 1! = 0,2707
- P(X=2) = 2 2 * e – 2 / 2! = 0,2707
- P(X=3) = 2 3 * e – 2/3 ! = 0,1805
Переглянути PMF
Ми часто візуалізуємо функції ймовірнісної маси за допомогою гістограм.
Наприклад, наступна гістограма показує ймовірності, пов’язані з кількістю народжень на годину для розподілу Пуассона, описаного в попередньому прикладі:

Зауважте, що кількість народжень може тривати до безкінечності, але ймовірності стають настільки малими після 10, що ви навіть не можете побачити їх на гістограмі.
Властивості PMF
Функція маси ймовірності має такі властивості:
1. Усі ймовірності позитивні для підтримки. Наприклад, ймовірність того, що кубик випаде між 1 і 6, є позитивною, а ймовірність усіх інших результатів дорівнює нулю.
2. Усі результати мають ймовірність від 0 до 1. Наприклад, ймовірність того, що кубик випаде між 1 і 6, становить 1/6, або 0,1666666 для кожного результату.
3. Сума всіх ймовірностей повинна дорівнювати 1. Наприклад, сума ймовірностей того, що кубик випаде на певне число, дорівнює 1/6 + 1/6 + 1/6 + 1/6 + 1/6 + 1. /6 = 1.
Додаткові ресурси
Що таке випадкові величини?
CDF чи PDF: у чому різниця?
Введення в біноміальний розподіл
Введення в розподіл Пуассона