Як створити коваріаційну матрицю в python

Коваріація — це міра того, як зміни в одній змінній пов’язані зі змінами в другій змінній. Точніше, це міра ступеня лінійного зв’язку двох змінних.

Коваріаційна матриця – це квадратна матриця, яка показує коваріацію між багатьма різними змінними. Це може бути корисним способом зрозуміти, як різні змінні пов’язані в наборі даних.

У наступному прикладі показано, як створити коваріаційну матрицю в Python.

Як створити коваріаційну матрицю в Python

Виконайте наступні кроки, щоб створити коваріаційну матрицю в Python.

Крок 1: Створіть набір даних.

Спочатку ми створимо набір даних, що містить тестові результати 10 різних учнів із трьох предметів: математики, природничих наук та історії.

 import numpy as np

math = [84, 82, 81, 89, 73, 94, 92, 70, 88, 95]
science = [85, 82, 72, 77, 75, 89, 95, 84, 77, 94]
history = [97, 94, 93, 95, 88, 82, 78, 84, 69, 78]

data = np.array([math, science, history])

Крок 2: Створіть коваріаційну матрицю.

Далі ми створимо коваріаційну матрицю для цього набору даних за допомогою функції numpy cov() , вказавши, що bias = True , щоб ми могли обчислити коваріаційну матрицю сукупності.

 np.cov(data, bias= True )

array([[ 64.96, 33.2, -24.44],
       [33.2, 56.4, -24.1],
       [-24.44, -24.1, 75.56]])

Крок 3: Інтерпретація коваріаційної матриці.

Значення вздовж діагоналей матриці є просто дисперсіями кожного предмета. Наприклад:

• Дисперсія балів з математики – 64,96
• Дисперсія балів з природничих наук становить 56,4
• Історична дисперсія балів становить 75,56

Інші значення матриці представляють коваріації між різними предметами. Наприклад:

• Коваріація між балами з математики та природничих наук становить 33,2.
• Коваріація між балами з математики та історії становить -24,44.
• Коваріація між балами з науки та історії становить -24,1.

Додатне число для коваріації вказує на те, що дві змінні мають тенденцію до збільшення або зменшення в тандемі. Наприклад, математика та природничі науки мають позитивну коваріацію (33,2), що вказує на те, що учні, які мають високі результати з математики, також, як правило, мають високі результати з природничих наук. Навпаки, учні, які мають погані результати в математиці, також, як правило, мають погані результати в науках.

Від’ємне число для коваріації вказує на те, що коли одна змінна збільшується, друга змінна має тенденцію до зменшення. Наприклад, математика та історія мають негативну коваріацію (-24,44), що вказує на те, що учні, які мають високі результати з математики, зазвичай отримують низькі результати з історії. Навпаки, учні, які мають низькі результати з математики, зазвичай отримують високі результати з історії.

Крок 4: Візуалізуйте коваріаційну матрицю (необов’язково).

Ви можете візуалізувати коваріаційну матрицю за допомогою функції heatmap() пакету seaborn:

 import seaborn as sns
import matplotlib.pyplot as plt

cov = np.cov(data, bias=True)
labs = ['math', 'science', 'history']

sns.heatmap(cov, annot=True, fmt='g', xticklabels=labs, yticklabels=labs)
plt.show()

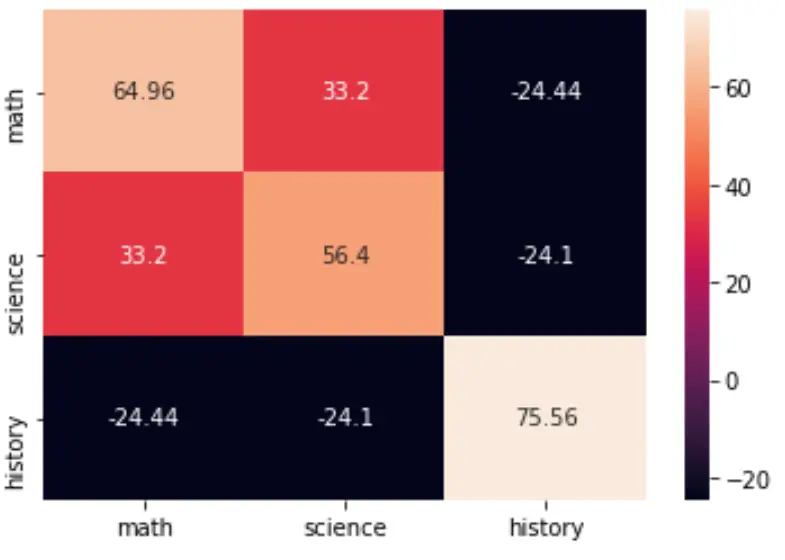
Ви також можете змінити палітру кольорів, вказавши аргумент cmap :

 sns.heatmap(cov, annot=True, fmt='g', xticklabels=labs, yticklabels=labs, cmap=' YlGnBu ')
plt.show() 

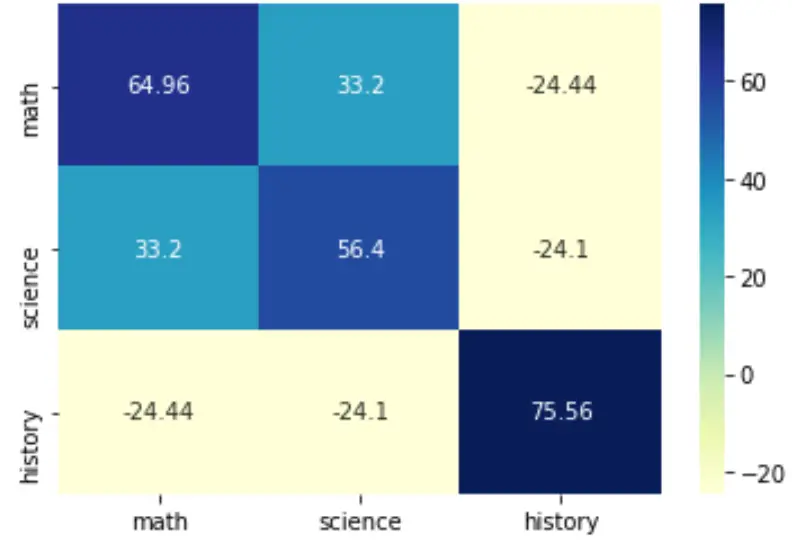
Щоб отримати докладніші відомості про те, як стилізувати цю теплову карту, зверніться до документації seaborn .