Rmse проти r-квадрату: який показник вам слід використовувати?

Регресійні моделі використовуються для кількісного визначення зв’язку між однією або декількома змінними предиктора та змінною відповіді.

Щоразу, коли ми підбираємо регресійну модель, ми хочемо зрозуміти, наскільки добре модель «відповідає» даним. Іншими словами, наскільки добре модель здатна використовувати значення змінних предикторів для прогнозування значення змінної відповіді ?

Двома показниками, які статистики часто використовують для кількісного визначення того, наскільки добре модель відповідає набору даних, є середньоквадратична помилка (RMSE) і R квадрат ( ^R2 ), які обчислюються таким чином:

RMSE : показник, який повідомляє нам, наскільки далекі передбачувані значення від спостережуваних значень у наборі даних у середньому. Чим нижче RMSE, тим краще модель відповідає набору даних.

Він розраховується таким чином:

RMSE = √ Σ(P _i – O _i ) ² / n

золото:

• Σ – символ, що означає «сума»
• P _i – прогнозоване значення для ^i-го спостереження
• O _i – спостережене значення для ^i-го спостереження
• n – розмір вибірки

R ² : метрика, яка повідомляє нам, яку частину дисперсії у змінній відповіді регресійної моделі можна пояснити змінними предикторами. Це значення становить від 0 до 1. Чим вище значення R ² , тим краще модель відповідає набору даних.

Він розраховується таким чином:

^R2 = 1 – (RSS/TSS)

золото:

• RSS являє собою суму квадратів залишків
• TSS представляє загальну суму квадратів

RMSE проти R ² : який показник вам слід використовувати?

Оцінюючи відповідність моделі набору даних, корисно обчислити як значення середнього середнього середнього квадратичного значення, так і значення R ² , оскільки кожен показник говорить нам щось інше.

З одного боку, RMSE повідомляє нам типову відстань між прогнозованим значенням, зробленим регресійною моделлю, та справжнім значенням.

З іншого боку, R ² говорить нам, якою мірою змінні-прогнози можуть пояснити варіацію змінної відповіді.

Наприклад, припустімо, що у нас є такий набір даних, який відображає інформацію про будинки в певному місті:

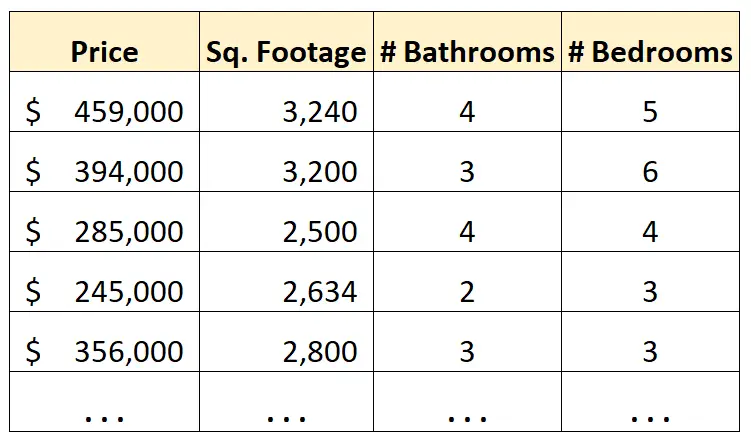
Тепер припустімо, що ми хочемо використовувати квадратні метри, кількість ванних кімнат і кількість спалень, щоб передбачити ціну будинку.

Ми можемо адаптувати наступну модель регресії:

Ціна = β ₀ + β ₁ (квадратний фут) + β ₂ (# ванних кімнат) + β ₃ (# спалень)

Тепер припустімо, що ми підбираємо цю модель, а потім обчислюємо такі показники, щоб оцінити відповідність моделі:

• RMSE : 14,342
• ^R2 : 0,856

Значення RMSE говорить нам, що середня різниця між прогнозованою моделлю ціною будинку та фактичною ціною будинку становить 14 342 долари.

Значення R ² говорить нам про те, що прогностичні змінні моделі (квадратні метри, кількість ванних кімнат і кількість спалень) можуть пояснити 85,6% варіації цін на житло.

Щоб визначити, чи є ці значення «хорошими» чи ні, ми можемо порівняти ці вимірювання з альтернативними моделями.

Наприклад, припустімо, що ми підбираємо іншу модель регресії, яка використовує інший набір змінних предикторів, і обчислюємо такі показники для цієї моделі:

• RMSE : 19,355
• ^R2 : 0,765

Ми бачимо, що значення RMSE цієї моделі вище, ніж у попередньої моделі. Також можна побачити, що значення R ² цієї моделі нижче, ніж у попередньої моделі. Це говорить нам про те, що ця модель гірше відповідає даним, ніж попередня модель.

Резюме

Ось основні моменти, порушені в цій статті:

• RMSE і R ² кількісно визначають, наскільки регресійна модель відповідає набору даних.
• RMSE говорить нам, наскільки добре регресійна модель може передбачити значення змінної відповіді в абсолютних виразах, тоді як R ² говорить нам, наскільки добре модель може передбачити значення змінної відповіді у відсотковому вираженні.
• Корисно обчислювати як RMSE, так і ^R2 для даної моделі, оскільки кожен показник дає нам корисну інформацію.

Додаткові ресурси

Вступ до множинної лінійної регресії
R проти R-Square: у чому різниця?
Що таке хороше значення R-квадрат?