Як створити кореляційну матрицю в sas (з прикладом)

Кореляційна матриця – це квадратна таблиця, яка показує коефіцієнти кореляції між змінними в наборі даних.

Це забезпечує швидкий спосіб зрозуміти міцність лінійних зв’язків, які існують між змінними в наборі даних.

Ви можете використовувати оператор PROC CORR у SAS, щоб створити кореляційну матрицю для заданого набору даних:

 /*create correlation matrix using all numeric variables in my_data*/
proc corr data =my_data;
run ;

За замовчуванням буде створено матрицю, яка відображає коефіцієнти кореляції між усіма числовими змінними в наборі даних.

Щоб включити в кореляційну матрицю лише певні змінні, ви можете скористатися оператором VAR :

 /*create correlation matrix using only var1, var2 and var3 in my_data*/
proc corr data =my_data;
    var var1, var2, var3;
run ;

У наступному прикладі показано, як створити кореляційну матрицю в SAS.

Приклад: створення кореляційної матриці в SAS

Припустімо, що в SAS є такий набір даних, який містить інформацію про різних баскетболістів:

 /*create dataset*/
data my_data;
    input team $ assists rebounds points;
    datalines ;
A 4 12 22
A 5 14 24
A 5 13 26
A 6 7 26
B 7 8 29
B 8 8 32
B 8 9 20
B 10 13 14
;
run ;

/*view dataset*/
proc print data =my_data; 

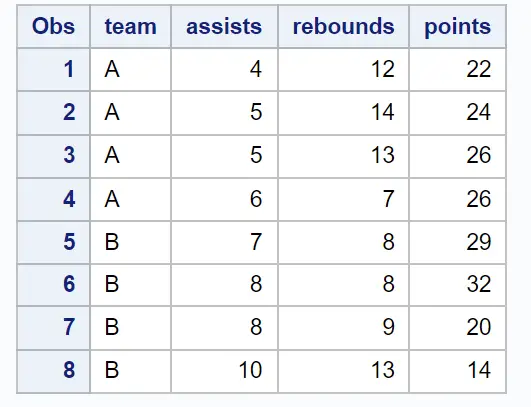
Ми можемо використовувати оператор PROC CORR , щоб створити кореляційну матрицю, яка за замовчуванням включає кожну числову змінну в наборі даних:

 /*create correlation matrix using all numeric variables in my_data*/
proc corr data =my_data;
run ; 

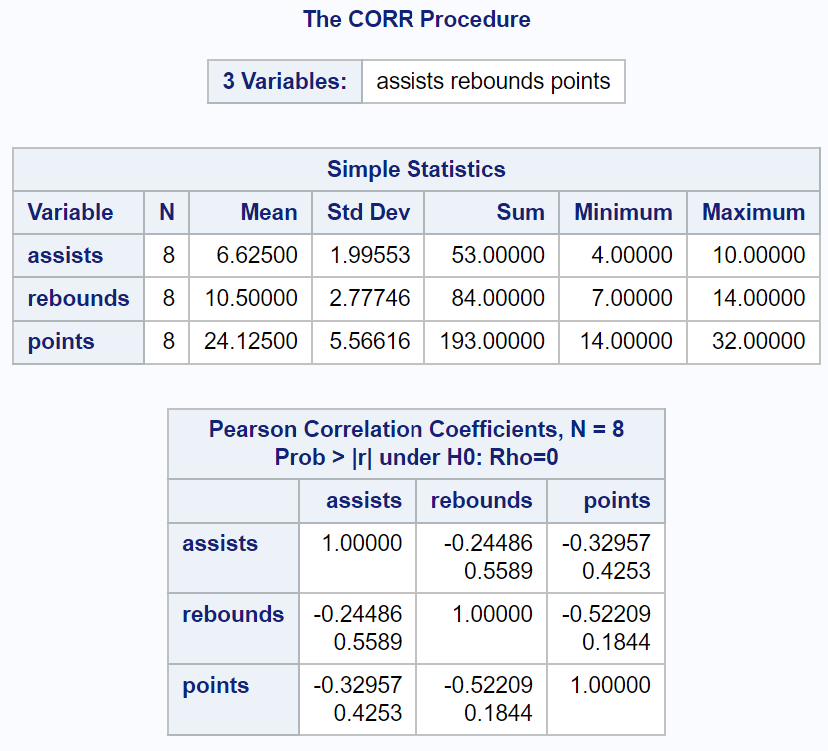
На виході відображається зведена статистика числових змінних у першій таблиці разом із кореляційною матрицею.

Зауважте, що змінна «команда» не була включена в кореляційну матрицю, оскільки вона не була числовою змінною.

Ось як інтерпретувати значення кореляційної матриці:

(1) Коефіцієнт кореляції Пірсона (r) між передачами та підбираннями становить -0,24486 . Відповідне значення p становить 0,5589 .

Оскільки r менше нуля, це говорить нам про те, що між цими двома змінними існує негативний лінійний зв’язок. Однак p-значення не менше 0,05, тому ця кореляція не є статистично значущою.

(2) Коефіцієнт кореляції Пірсона (r) між передачами та очками становить -0,32957 . Відповідне значення p становить 0,4253 .

Між цими двома змінними існує негативний лінійний зв’язок, але він не є статистично значущим.

(3) Коефіцієнт кореляції Пірсона (r) між підбираннями та очками становить -0,52209 . Відповідне значення p становить 0,1844 .

Між цими двома змінними існує негативний лінійний зв’язок, але він не є статистично значущим.

Зверніть увагу, що ми також можемо використовувати оператор VAR , щоб включити лише певні числові змінні в кореляційну матрицю:

 /*create correlation matrix using only assists and rebounds variables*/
proc corr data =my_data;
    var assists rebounds;
run ; 

Зверніть увагу, що в цю кореляційну матрицю були включені лише змінні передачі та підбирання .

Додаткові ресурси

У наступних посібниках пояснюється, як виконувати інші типові завдання в SAS:

Як створити матрицю діаграми розсіювання в SAS
Як створити зведені таблиці в SAS
Як розрахувати коефіцієнт інфляції дисперсії (VIF) у SAS