Як виконати тест шапіро-вілка в r (з прикладами)

Тест Шапіро-Вілка є тестом нормальності. Він використовується для визначення того, чи походить вибірка з нормального розподілу .

Цей тип перевірки корисний для визначення того, чи походить даний набір даних із нормального розподілу, що є загальноприйнятим припущенням у багатьох статистичних тестах, включаючи регресію , дисперсійний аналіз , t-тести та багато інших. ‘інші.

Ми можемо легко виконати тест Шапіро-Вілка на заданому наборі даних за допомогою наступної вбудованої функції в R:

shapiro.test(x)

золото:

• x: числовий вектор значень даних.

Ця функція створює тестову статистику W разом із відповідним p-значенням. Якщо p-значення менше α = 0,05, є достатньо доказів, щоб стверджувати, що вибірка не з нормально розподіленої сукупності.

Примітка. Для використання функції shapiro.test() розмір вибірки має бути від 3 до 5000.

Цей підручник демонструє кілька прикладів практичного використання цієї функції.

Приклад 1: Тест Шапіро-Вілка за нормальними даними

У наступному коді показано, як виконати тест Шапіро-Вілка на наборі даних із розміром вибірки n=100:

 #make this example reproducible
set.seed(0)

#create dataset of 100 random values generated from a normal distribution
data <- rnorm(100)

#perform Shapiro-Wilk test for normality
shapiro.test(data)

	Shapiro-Wilk normality test

data:data
W = 0.98957, p-value = 0.6303

P-значення тесту виявляється рівним 0,6303 . Оскільки це значення не менше 0,05, ми можемо припустити, що дані вибірки надходять із нормально розподіленої сукупності.

Цей результат не повинен бути несподіваним, оскільки ми створили вибіркові дані за допомогою функції rnorm(), яка генерує випадкові значення з нормального розподілу із середнім значенням = 0 і стандартним відхиленням = 1.

Пов’язане: посібник із dnorm, pnorm, qnorm і rnorm у R

Ми також можемо створити гістограму, щоб візуально перевірити, що вибіркові дані розподілені нормально:

 hist(data, col=' steelblue ') 

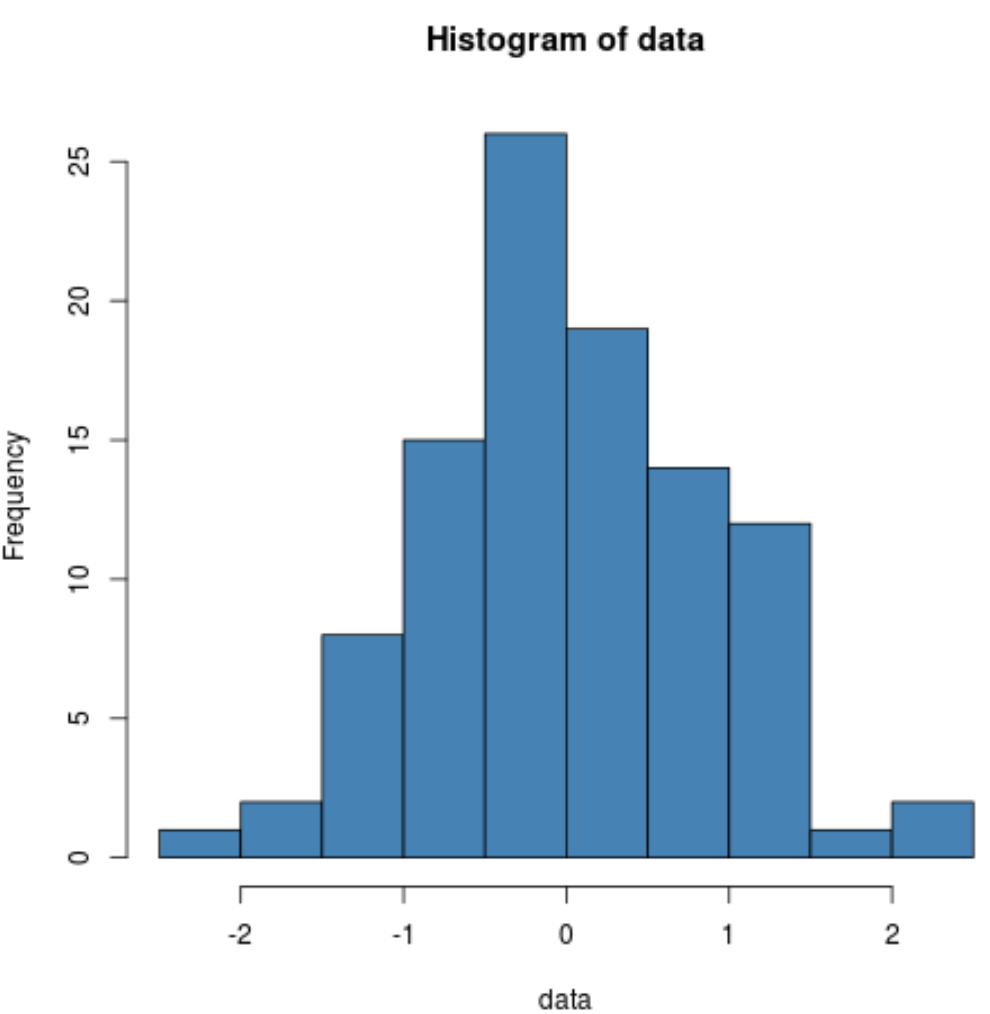
Ми бачимо, що розподіл має досить дзвоноподібну форму з піком у центрі розподілу, що є типовим для нормально розподілених даних.

Приклад 2: тест Шапіро-Вілка на ненормальних даних

У наступному коді показано, як виконати тест Шапіро-Вілка на наборі даних із розміром вибірки n=100, у якому значення випадково генеруються з розподілу Пуассона :

 #make this example reproducible
set.seed(0)

#create dataset of 100 random values generated from a Poisson distribution
data <- rpois(n=100, lambda=3)

#perform Shapiro-Wilk test for normality
shapiro.test(data)

	Shapiro-Wilk normality test

data:data
W = 0.94397, p-value = 0.0003393

P-значення тесту виявляється рівним 0,0003393 . Оскільки це значення менше 0,05, ми маємо достатньо доказів, щоб стверджувати, що дані вибірки не походять із нормально розподіленої сукупності.

Цей результат не повинен дивувати, оскільки ми згенерували вибіркові дані за допомогою функції rpois(), яка генерує випадкові значення з розподілу Пуассона.

Пов’язане: посібник із dpois, ppois, qpois і rpois у R

Ми також можемо створити гістограму, щоб візуально побачити, що вибіркові дані не розподілені нормально:

 hist(data, col=' coral2 ') 

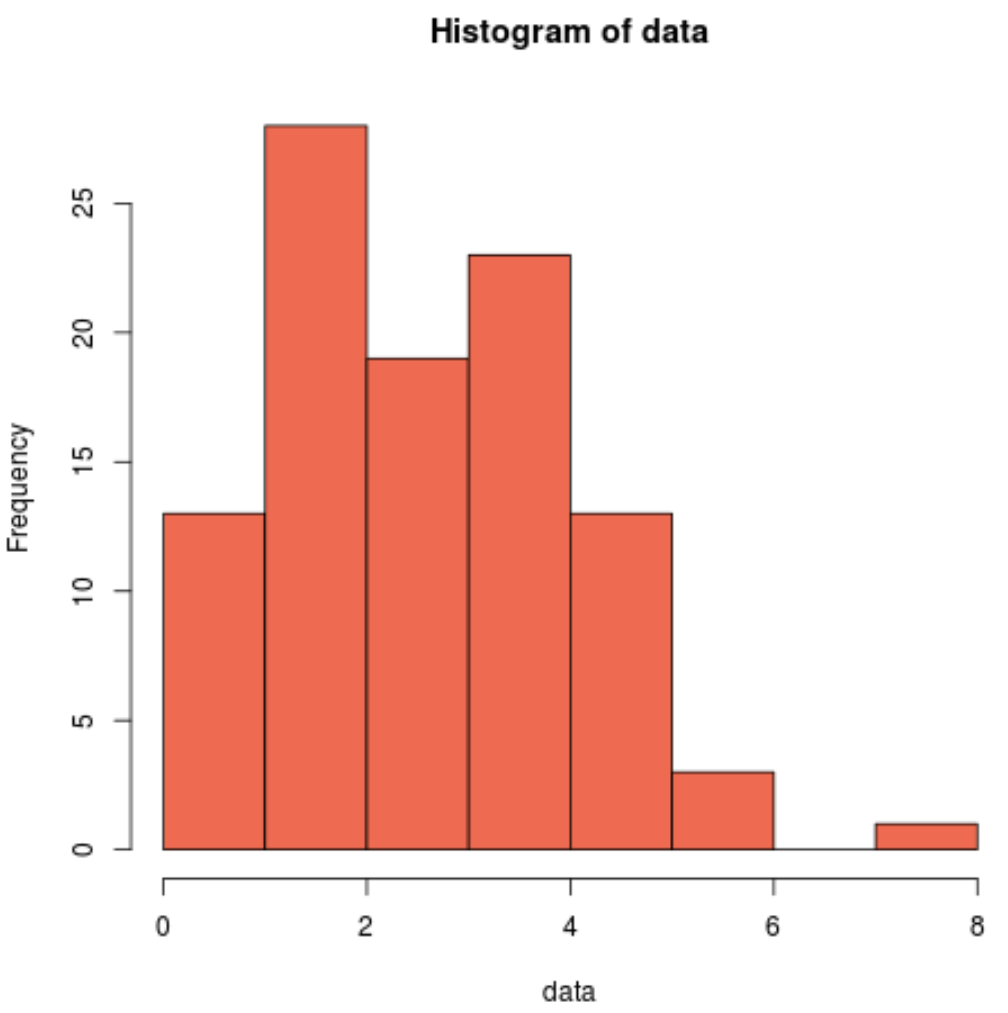
Ми бачимо, що розподіл має правий перекіс і не має типової «форми дзвона», пов’язаної з нормальним розподілом. Таким чином, наша гістограма відповідає результатам тесту Шапіро-Вілка та підтверджує, що наші вибіркові дані не походять із нормального розподілу.

Що робити з нестандартними даними

Якщо заданий набір даних розподілений ненормально , ми часто можемо виконати одне з наступних перетворень, щоб зробити його більш нормальним:

1. Перетворення журналу: перетворення змінної відповіді з y на log(y) .

2. Перетворення квадратного кореня: перетворення змінної відповіді з y на √y .

3. Перетворення кубічного кореня: перетворення змінної відповіді з y на y ^1/3 .

Виконуючи ці перетворення, змінна відповіді загалом наближається до нормального розподілу.

Ознайомтеся з цим посібником , щоб побачити, як виконати ці перетворення на практиці.

Додаткові ресурси

Як виконати тест Андерсона-Дарлінга в R
Як виконати пробу Колмогорова-Смирнова в Р
Як виконати тест Шапіро-Вілка на Python