Як розрахувати кореляцію рейтингу спірмена в google таблицях
У статистиці кореляція означає силу та напрямок зв’язку між двома змінними. Значення коефіцієнта кореляції може варіюватися від -1 до 1 з такими інтерпретаціями:
- -1: ідеальне негативне співвідношення між двома змінними
- 0: немає зв’язку між двома змінними
- 1: ідеальний позитивний зв’язок між двома змінними
Особливий тип кореляції називається ранговою кореляцією Спірмена , яка використовується для вимірювання кореляції між двома ранжованими змінними. (наприклад, рейтинг іспиту з математики студента відносно рангу його балу з іспиту з природничих наук у класі).
У цьому посібнику пояснюється, як обчислити кореляцію рангу Спірмена між двома змінними в Google Таблицях.
Приклад: кореляція рейтингу Спірмена в Google Таблицях
Виконайте наведені нижче кроки, щоб обчислити кореляцію рангу Спірмена між балом іспиту з математики та балом іспиту з природничих наук 10 учнів у певному класі.
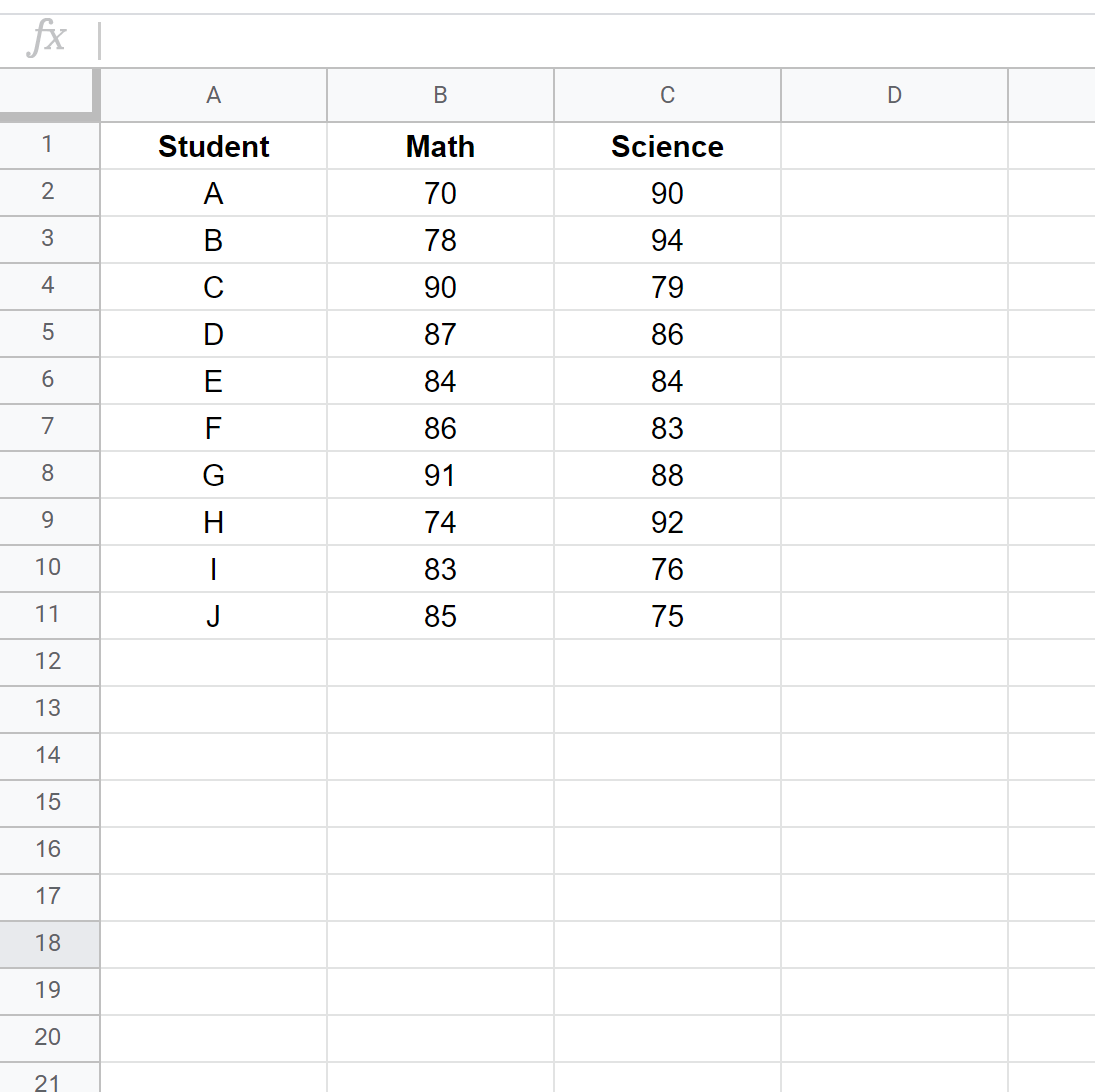
Крок 1: Введіть дані.
Введіть результати іспиту кожного студента в два окремі стовпці:
Крок 2: обчисліть рейтинг для кожного балу іспиту.
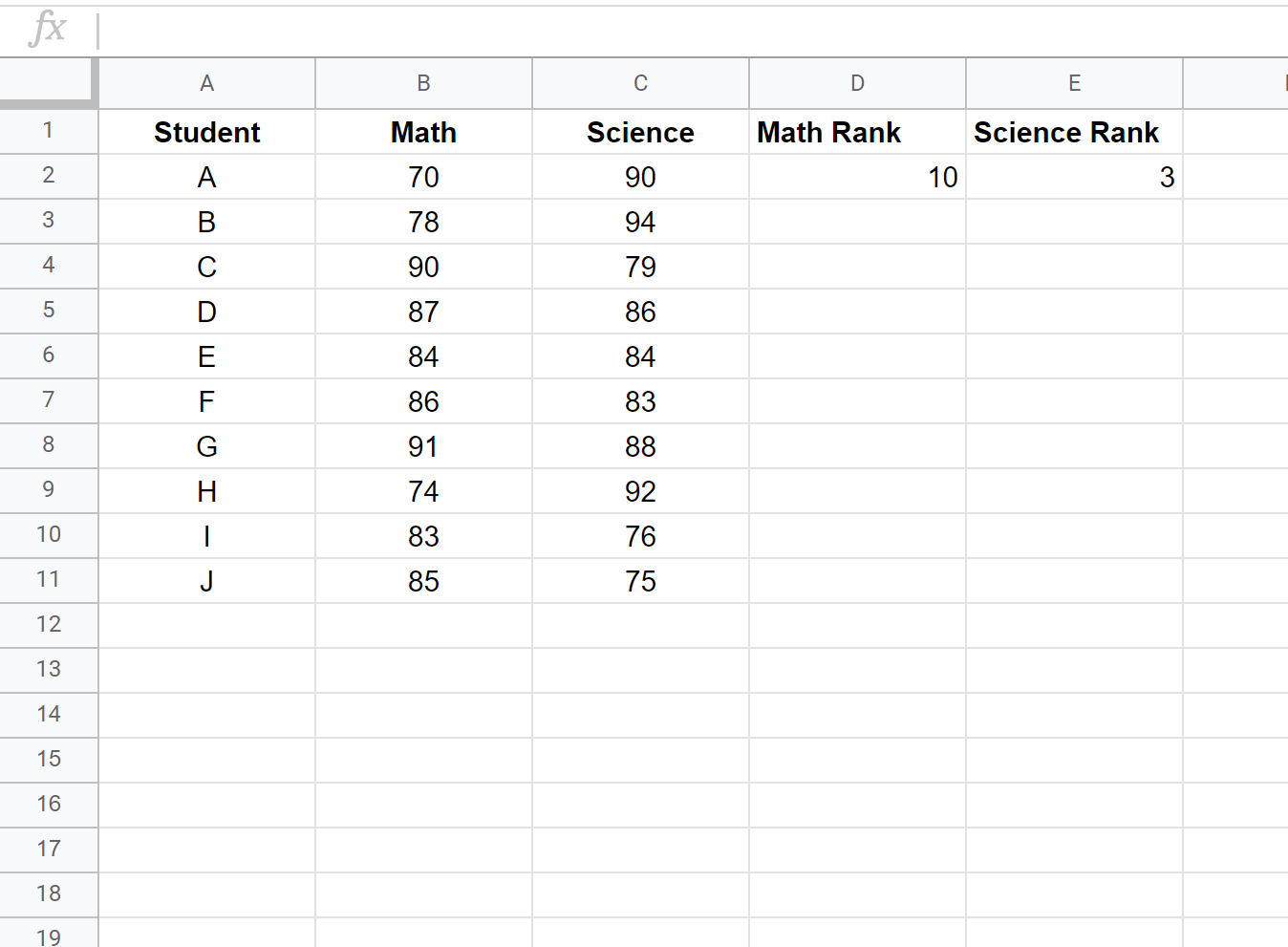
Далі ми розрахуємо рейтинг для кожного екзаменаційного балу. Використовуйте наступні формули в клітинках D2 і E2, щоб обчислити оцінки першого учня з математики та природничих наук:
Комірка D2: =RANK.AVG(B2, $B$2:$B$11, 0)
Комірка E2: =RANK.AVG(C2, $C$2:$C$11, 0)
Далі виділіть решту клітинок для заповнення:
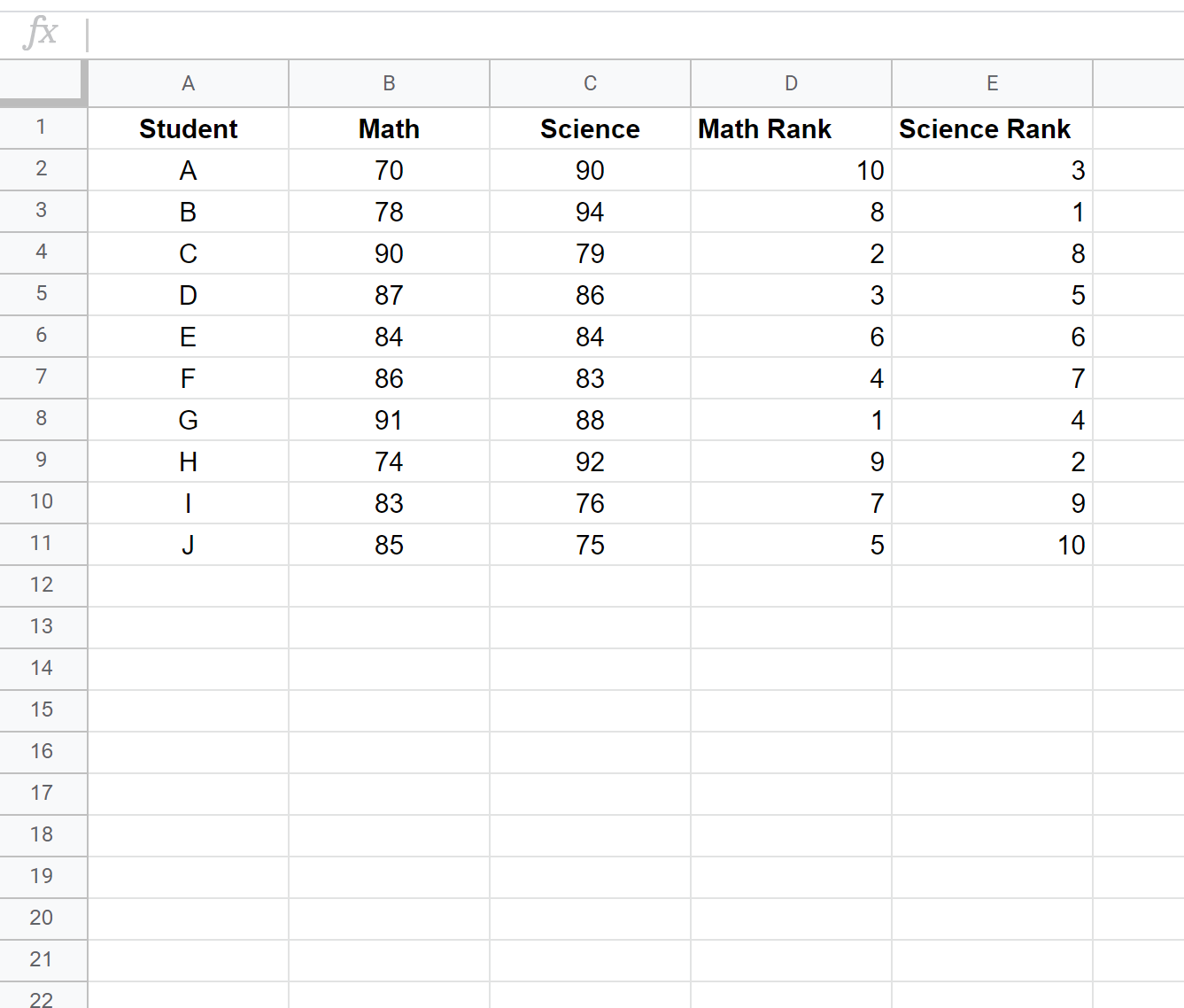
Потім натисніть Ctrl+D, щоб ввести рейтинги кожного студента:
Крок 3: Обчисліть коефіцієнт рангової кореляції Спірмена.
Нарешті, ми обчислимо коефіцієнт рангової кореляції Спірмена між балами з математики та балами з природничих наук за допомогою функції CORREL() :
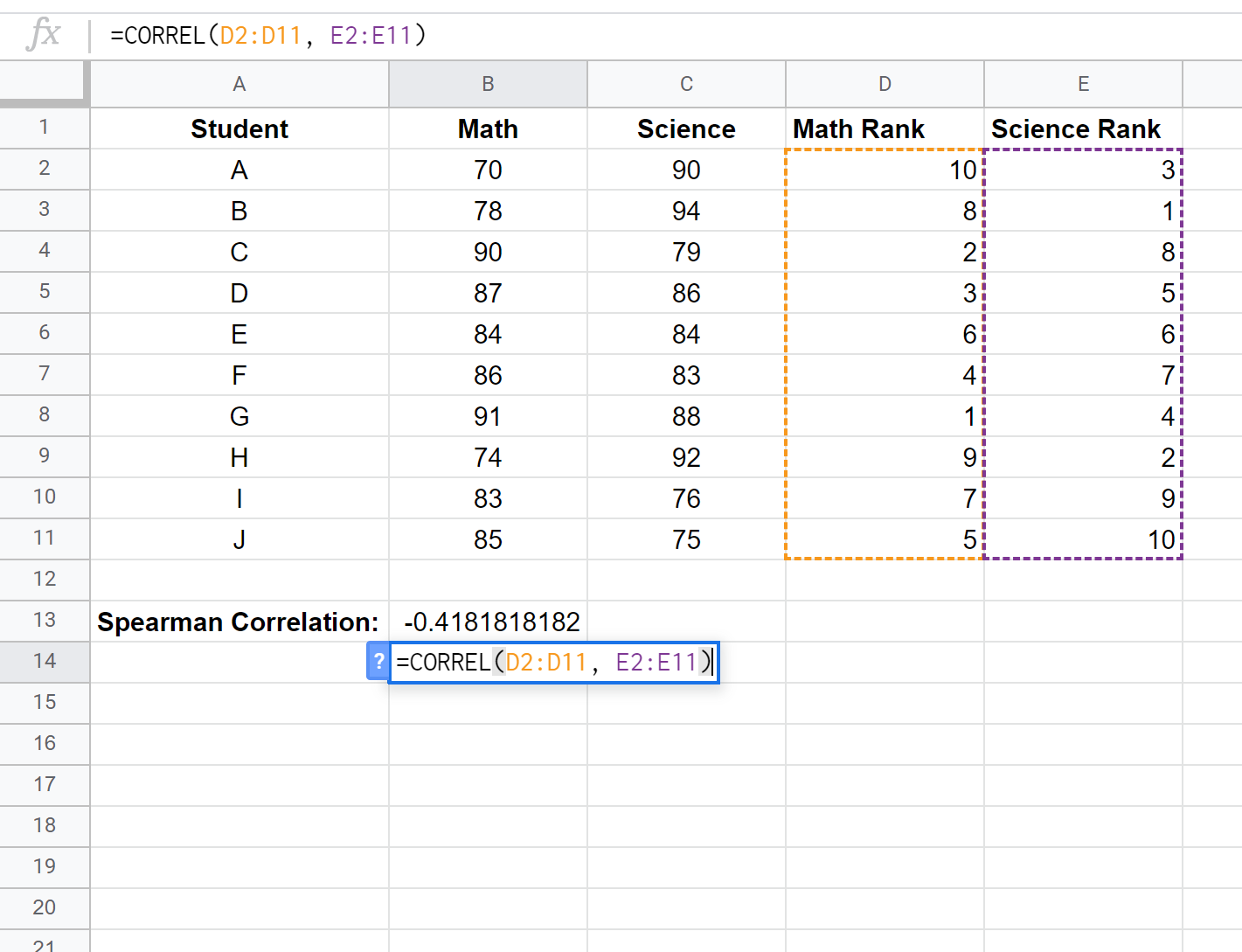
Рангова кореляція Спірмена дорівнює -0,41818 .
Крок 4 (необов’язково): визначте, чи є кореляція рангів Спірмена статистично значущою.
На попередньому кроці ми виявили, що рангова кореляція Спірмена між іспитовими балами з математики та природничих наук становила -0,41818 , що вказує на негативну кореляцію між двома змінними.
Однак, щоб визначити, чи є ця кореляція статистично значущою, нам потрібно буде звернутися до таблиці рангової кореляції критичних значень Спірмена, яка показує критичні значення, пов’язані з різними розмірами вибірки (n) і рівнями значущості (α).
Якщо абсолютне значення нашого коефіцієнта кореляції перевищує критичне значення в таблиці, то кореляція між двома змінними є статистично значущою.
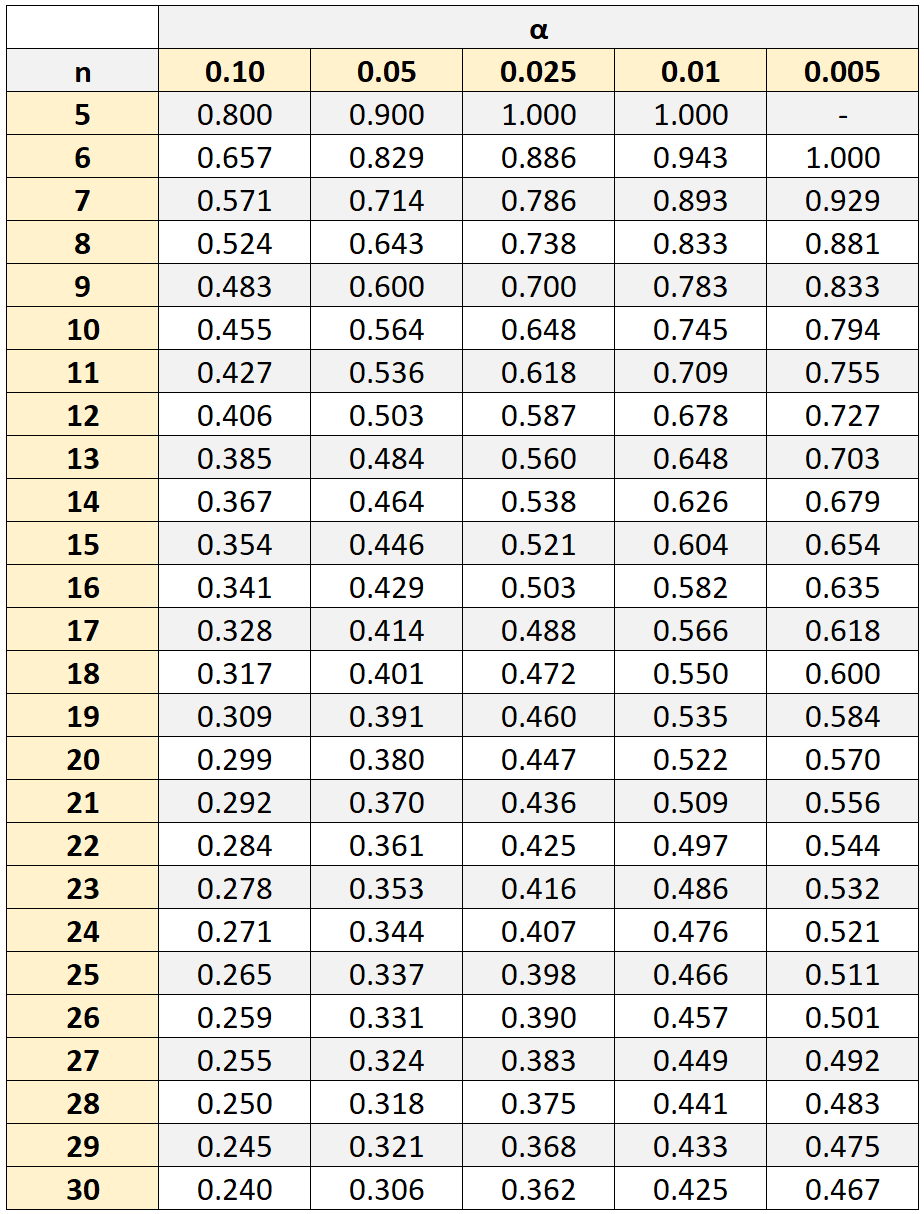
У нашому прикладі розмір нашої вибірки становив n = 10 студентів. Використовуючи рівень значущості 0,05, ми знаходимо, що критичне значення становить 0,564 .
Оскільки абсолютне значення розрахованого нами коефіцієнта рангової кореляції Спірмена ( 0,41818 ) не перевищує це критичне значення, це означає, що кореляція між балами з математики та природничих наук не є статистично значущою.