Як виконати квадратичну регресію в spss

Коли дві змінні мають лінійний зв’язок, ви часто можете використовувати просту лінійну регресію , щоб кількісно визначити їхній зв’язок.

Однак проста лінійна регресія не працює добре, коли дві змінні мають нелінійний зв’язок. У цих випадках ви можете спробувати використати квадратичну регресію .

У цьому посібнику пояснюється, як виконати квадратичну регресію в SPSS.

Приклад: квадратична регресія в SPSS

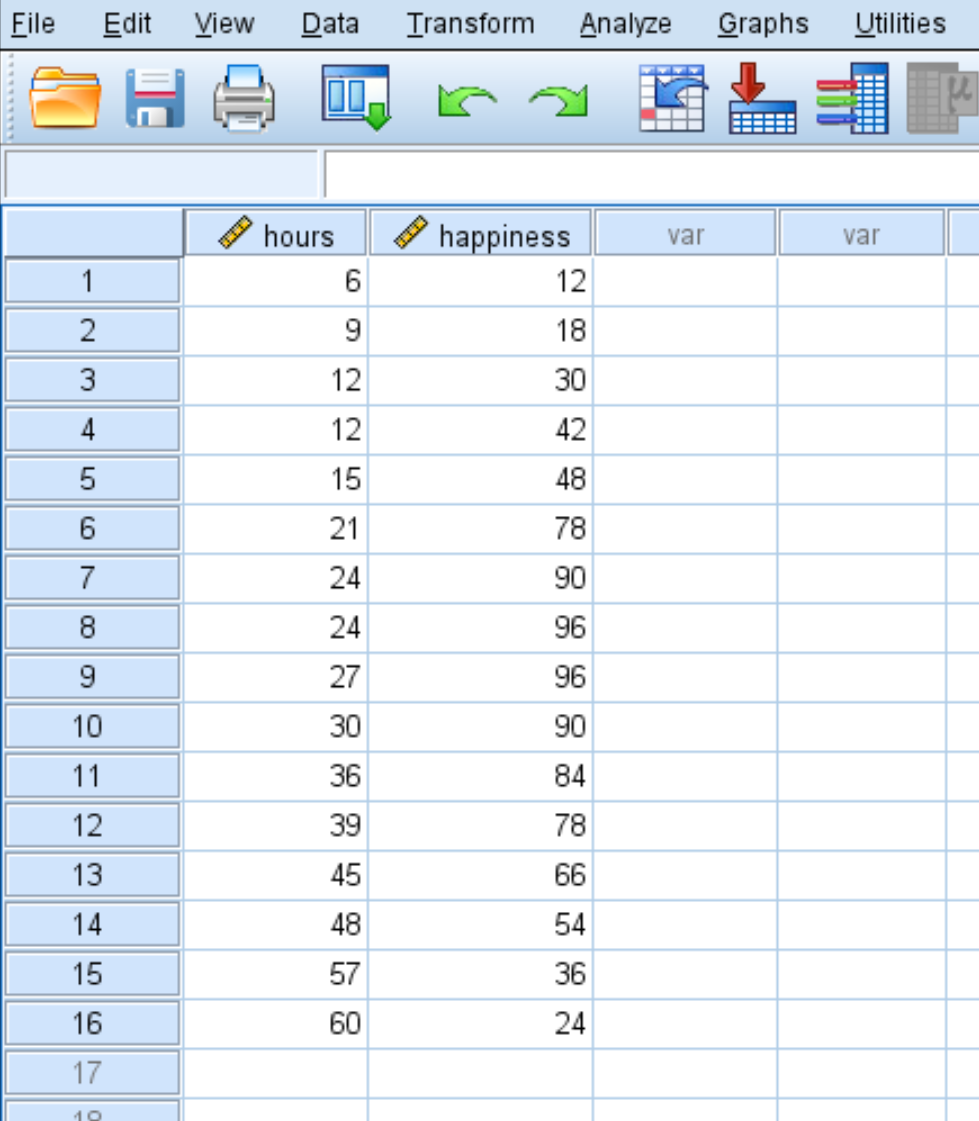
Припустімо, ми хочемо зрозуміти залежність між кількістю відпрацьованих годин і щастям. У нас є такі дані про кількість відпрацьованих годин на тиждень і рівень щастя (за шкалою від 0 до 100) для 16 різних людей:

Виконайте наступні кроки, щоб виконати квадратичну регресію в SPSS.

Крок 1: Візуалізуйте дані.

Перш ніж виконувати квадратичну регресію, давайте створимо діаграму розсіювання, щоб візуалізувати зв’язок між відпрацьованими годинами та щастям, щоб переконатися, що дві змінні насправді мають квадратичний зв’язок.

Перейдіть на вкладку «Діаграми» , а потім клацніть «Конструктор діаграм ».

У новому вікні, що з’явиться, виберіть Scatter/Dot зі списку Choose from . Потім перетягніть діаграму з позначкою Simple Scatter у головне вікно редагування. Перетягніть змінні години на вісь X і щастя на вісь Y. Потім натисніть OK .

З’явиться така діаграма розсіювання:

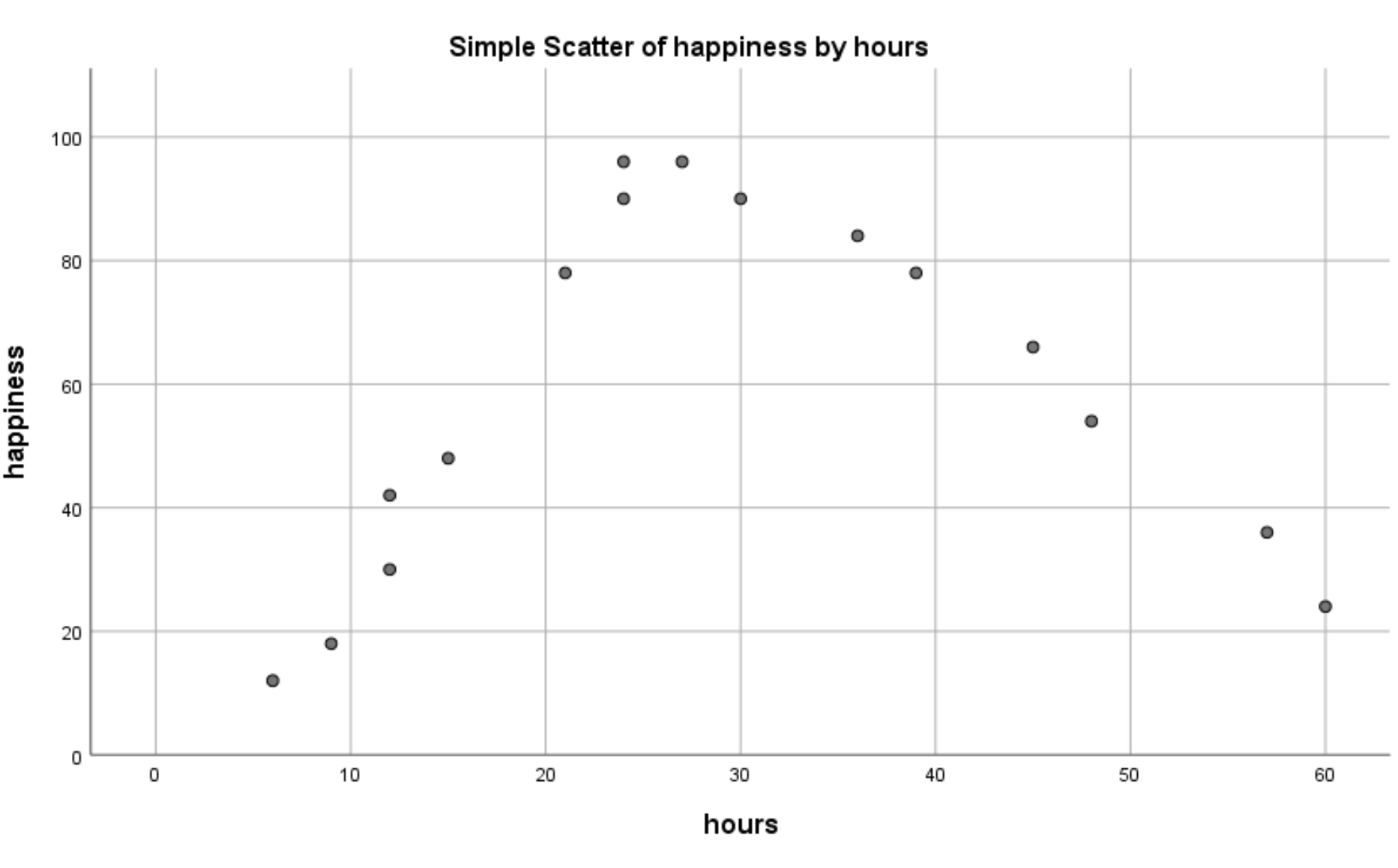
Ми чітко бачимо, що існує нелінійний зв’язок між відпрацьованими годинами та щастям. Це говорить нам про те, що квадратична регресія є відповідним методом для використання в цій ситуації.

Крок 2: Створіть нову змінну.

Перш ніж ми зможемо виконати квадратичну регресію, нам потрібно створити змінну предиктора для годин ² .

Клацніть вкладку «Трансформація» , а потім клацніть «Обчислити змінну» :

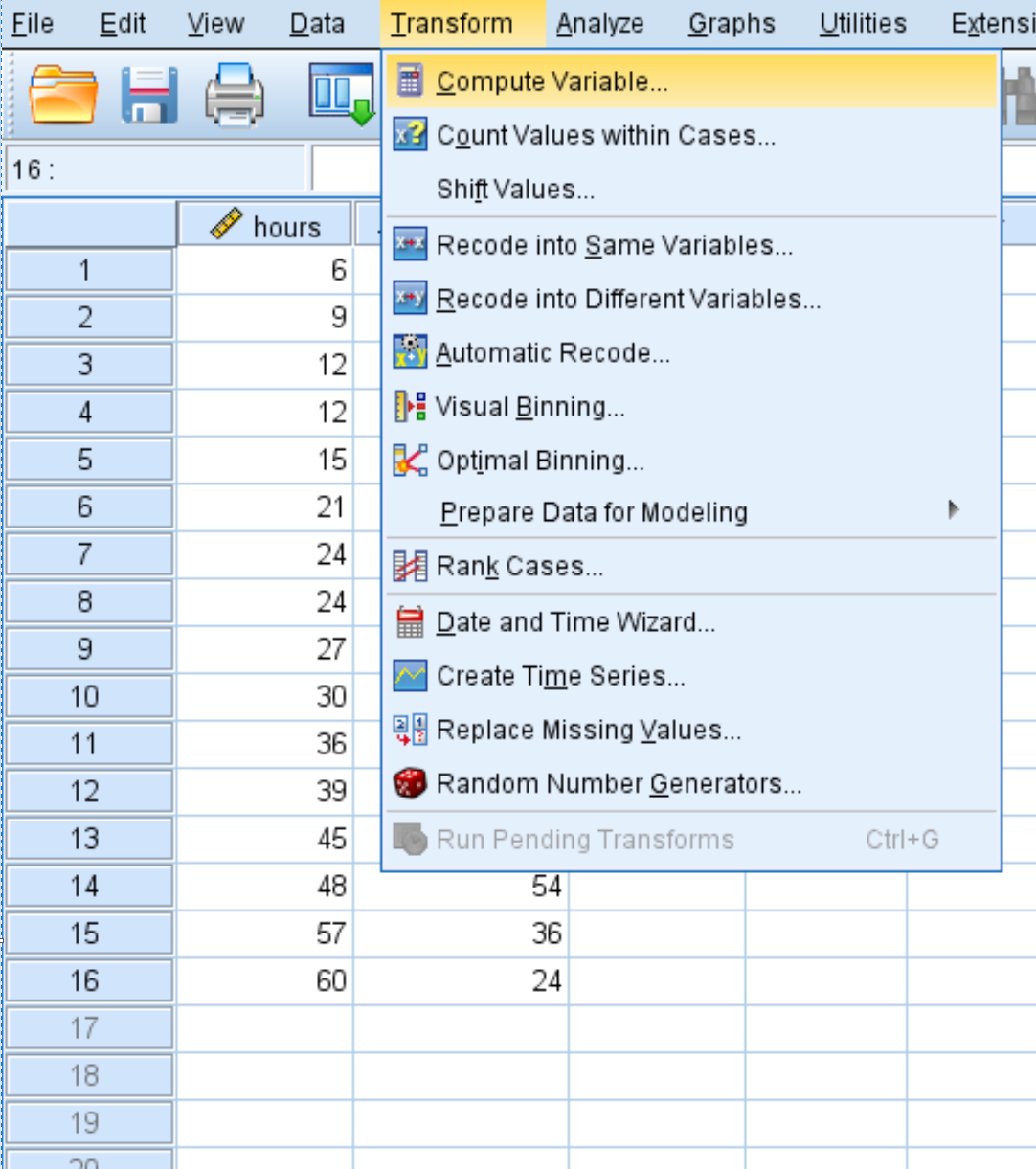
У новому вікні, що з’явиться, назвіть цільову змінну hours2 і встановіть для неї значення hours*hours :

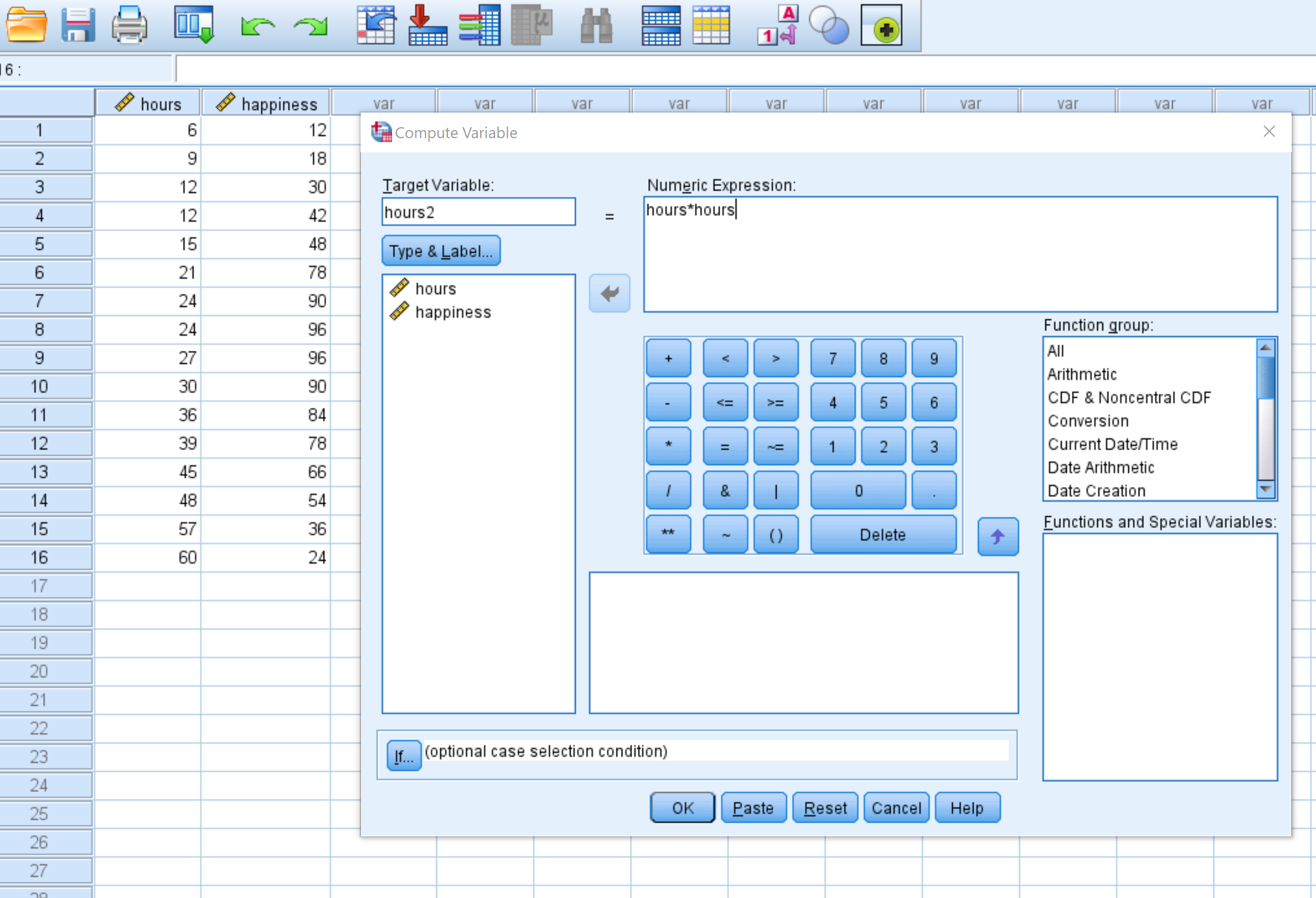
Після натискання кнопки OK змінна hours2 з’явиться в новому стовпці:

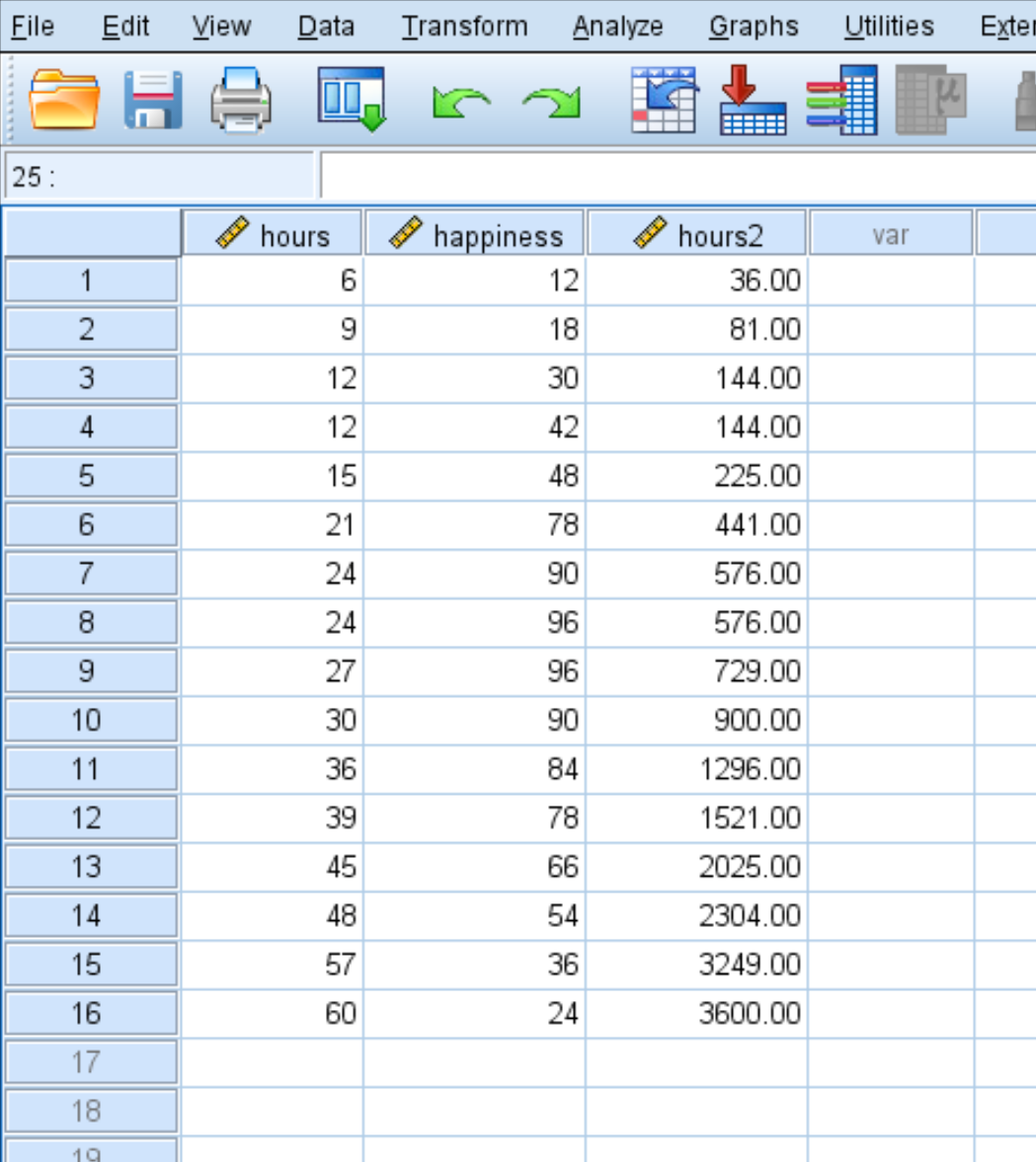
Крок 3: Виконайте квадратичну регресію.

Далі ми виконаємо квадратичну регресію. Натисніть вкладку «Аналіз» , потім «Регресія» , потім «Лінійна» :

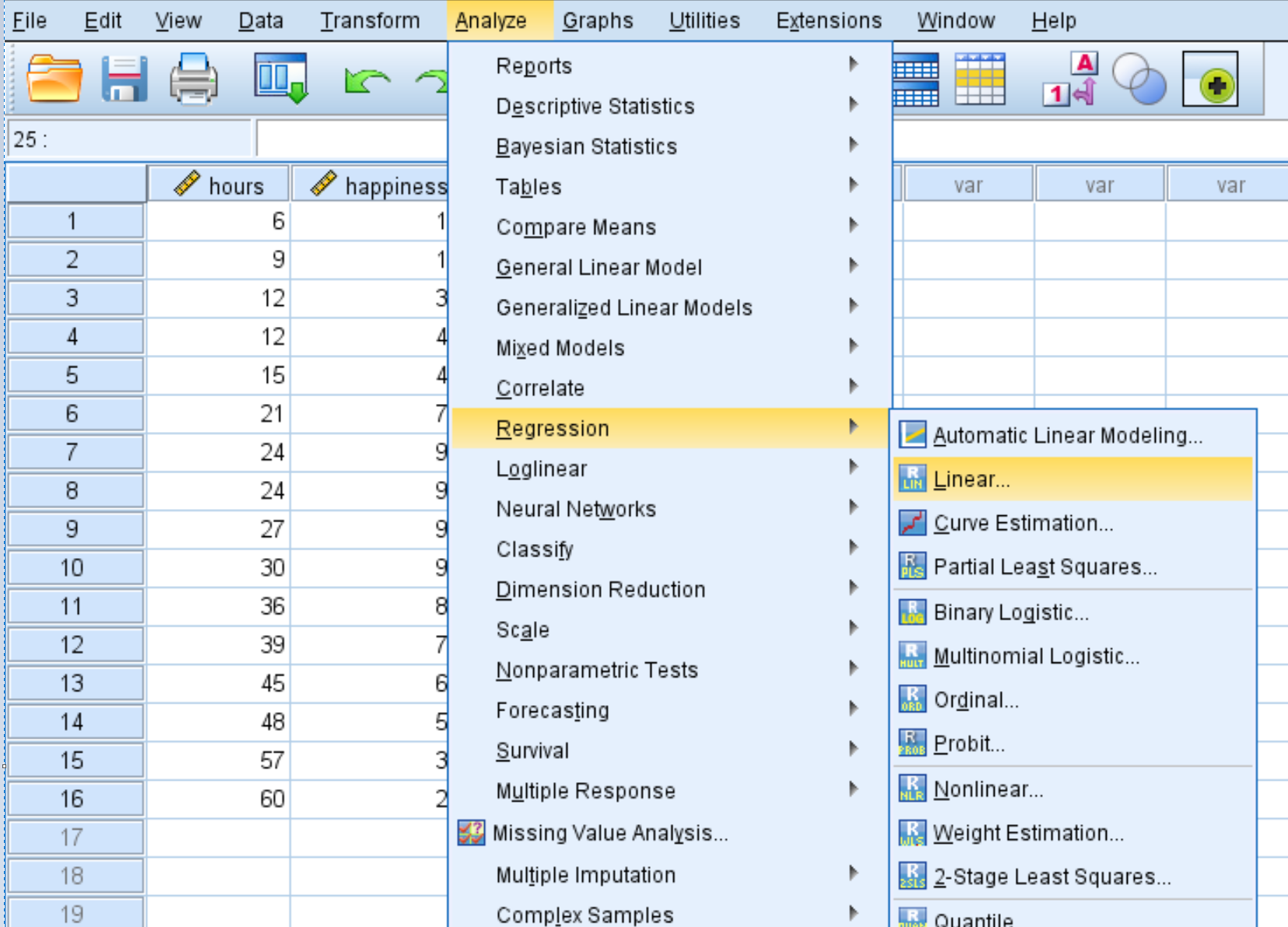
У новому вікні, що з’явиться, перетягніть щастя в поле з написом «Утриманець». Перетягніть Години та Години2 у поле з позначкою Незалежні. Потім натисніть OK .

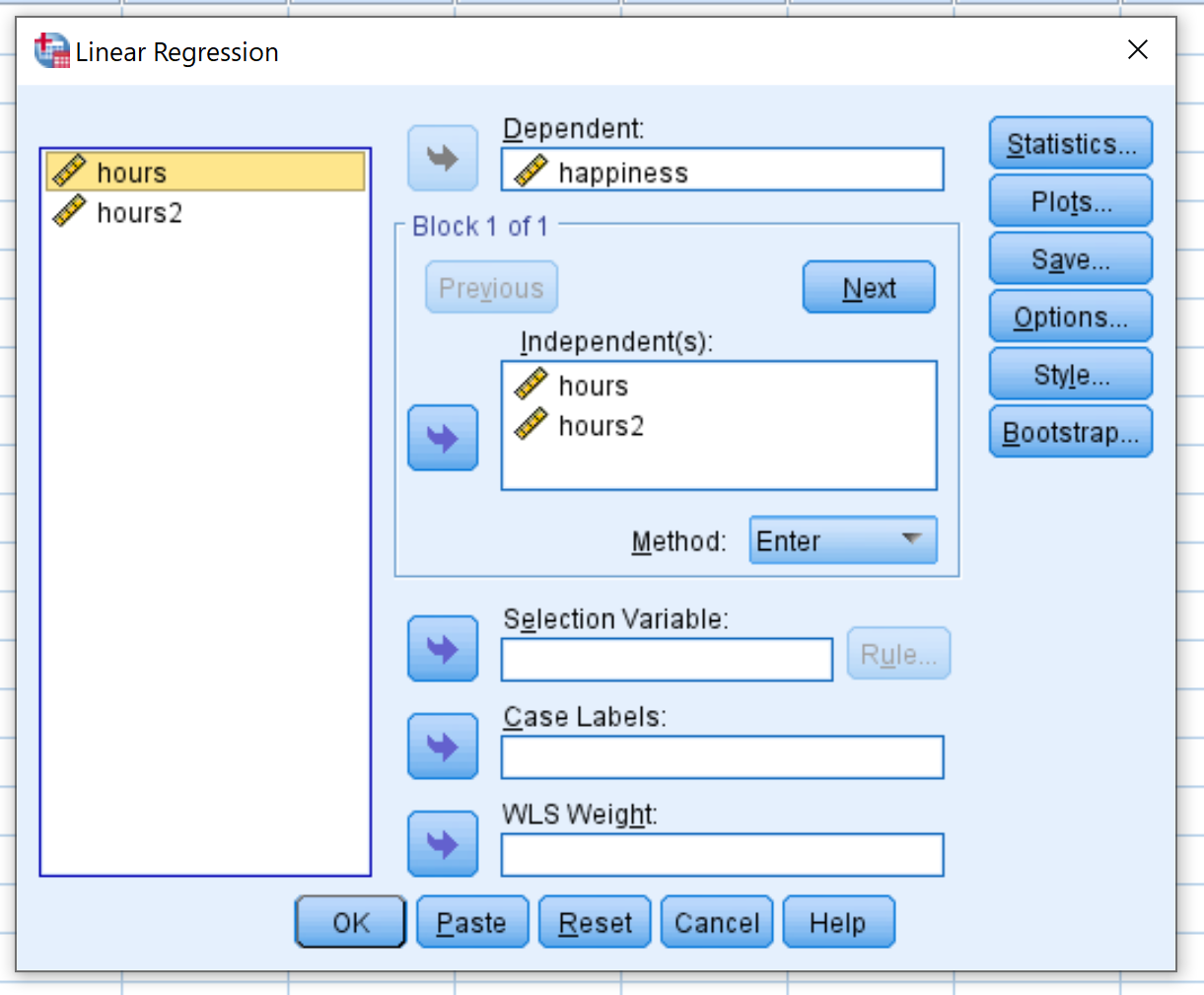
Крок 4: Інтерпретація результатів.

Після натискання кнопки OK результати квадратичної регресії з’являться в новому вікні.

Перша таблиця, яка нас цікавить, називається «Підсумок моделі» :

Ось як інтерпретувати найбільш відповідні цифри в цій таблиці:

• R Square: це частка дисперсії у змінній відповіді, яку можна пояснити пояснювальними змінними. У цьому прикладі 90,9% варіації щастя можна пояснити змінними годин і години ² .
• Стандартний. Похибка оцінки: стандартна помилка – це середня відстань між спостережуваними значеннями та лінією регресії. У цьому прикладі спостережувані значення відхиляються в середньому на 9519 одиниць від лінії регресії.

Наступна таблиця, яка нас цікавить, називається ANOVA :

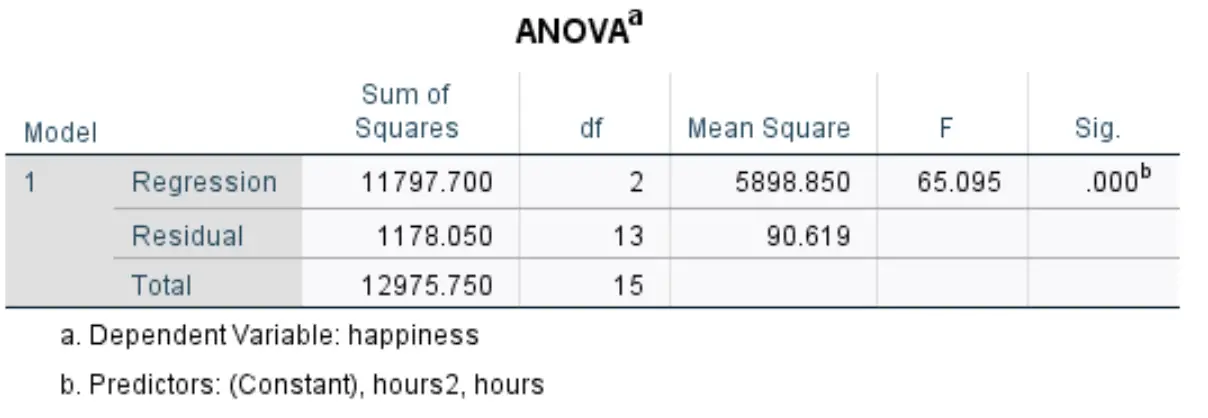
Ось як інтерпретувати найбільш відповідні цифри в цій таблиці:

• F: це загальна F-статистика для регресійної моделі, розрахована як середньоквадратична регресія / середньоквадратичний залишок.
• Sig: це p-значення, пов’язане із загальною статистикою F. Це говорить нам про те, чи є модель регресії в цілому статистично значущою чи ні. У цьому випадку p-значення дорівнює 0,000, що вказує на те, що пояснювальні змінні години та години ² разом мають статистично значущий зв’язок із результатом іспиту.

Наступна таблиця, яка нас цікавить, має назву Коефіцієнти :

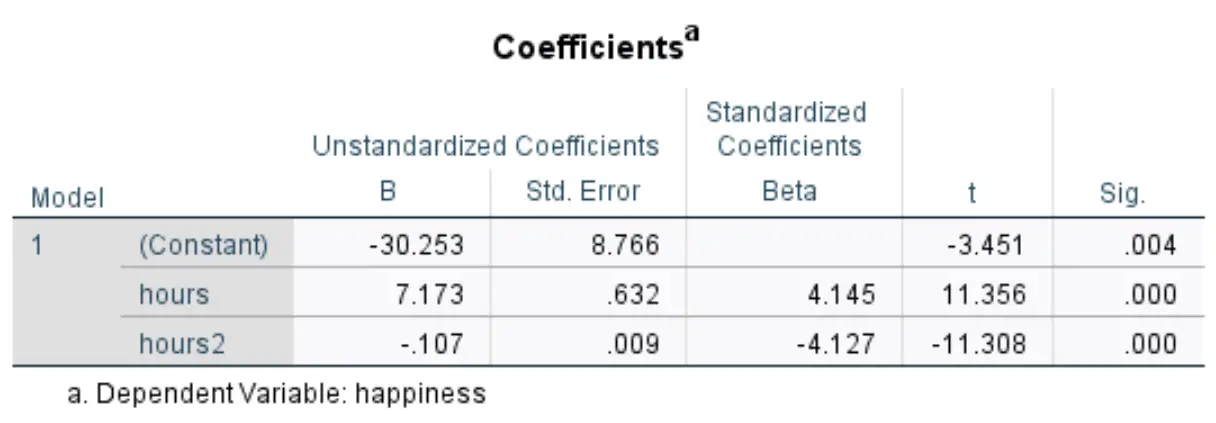
Ми можемо використовувати значення в стовпці Unstandardized B , щоб сформувати розрахункове рівняння регресії для цього набору даних:

Оцінений рівень щастя = -30,253 + 7,173*(години) – 0,107*( ² години)

Ми можемо використовувати це рівняння, щоб визначити передбачуваний рівень щастя людини на основі кількості відпрацьованих годин на тиждень. Наприклад, людина, яка працює 60 годин на тиждень, повинна мати рівень щастя 14,97:

Оцінений рівень щастя = -30,253 + 7,173*(60) – 0,107*(60 ² ) = 14,97 .

І навпаки, людина, яка працює 30 годин на тиждень, повинна мати рівень щастя 88,65:

Оцінений рівень щастя = -30,253 + 7,173*(30) – 0,107*(30 ² ) = 88,65 .

Крок 5: Повідомте про результати.

Нарешті, ми хочемо повідомити про результати нашої квадратичної регресії. Ось приклад того, як це зробити:

Було проведено квадратичну регресію, щоб кількісно визначити зв’язок між кількістю годин, які людина працювала, та її відповідним рівнем щастя (вимірюється від 0 до 100). Для аналізу була використана вибірка з 16 осіб.

Результати показали, що існує статистично значущий зв’язок між пояснювальними змінними години та години ² та змінною відповіді щастя (F(2, 13) = 65,095, p < 0,000).

Разом ці дві пояснювальні змінні спричинили 90,9% мінливості щастя.

Рівняння регресії вийшло таким:

Оцінений рівень щастя = -30,253 + 7,173 (години) – 0,107 ( ² години)